Anvendelser af differentialregning

Differentialregning bruges ikke kun til at beregne hældninger. Den giver også en dybere forståelse af, hvordan funktioner opfører sig. Ved at studere den afledte kan man bestemme, hvor en funktion stiger eller falder, finde dens maksimum og minimum, og analysere dens grafiske form. Metoden anvendes i alt fra fysik og økonomi til biologi og teknik.

Monotoni, hvor funktionen stiger og falder

Den afledte funktion $ \large f'(x) $ fortæller, om $ \large f(x) $ er stigende eller faldende i et givet interval:

Hvis $ \large f'(x) > 0 $, er funktionen stigende.
Hvis $ \large f'(x) < 0 $, er funktionen faldende.
Hvis $ \large f'(x) = 0 $, har funktionen et stationært punkt.

Et stationært punkt er et sted, hvor tangentens hældning er nul. Det kan være et lokalt maksimum, minimum eller et vendepunkt.

Eksempel: Analyse af en funktion

Undersøg funktionen $ \large f(x) = x^3 - 3x^2 + 2 $.

Først findes den afledte:

$$ \large f'(x) = 3x^2 - 6x = 3x(x - 2) $$

Den afledte er nul for $ \large x = 0 $ og $ \large x = 2 $. Vi undersøger fortegnet for $ \large f'(x) $ i intervallerne:

For $ \large x < 0 $: $ \large f'(x) > 0 $ → stigende
For $ \large 0 < x < 2 $: $ \large f'(x) < 0 $ → faldende
For $ \large x > 2 $: $ \large f'(x) > 0 $ → stigende

Dermed har funktionen et lokalt maksimum i $ \large x = 0 $ og et lokalt minimum i $ \large x = 2 $. Denne metode kaldes fortegnsskema og bruges til at finde, hvor funktionen vokser eller aftager.

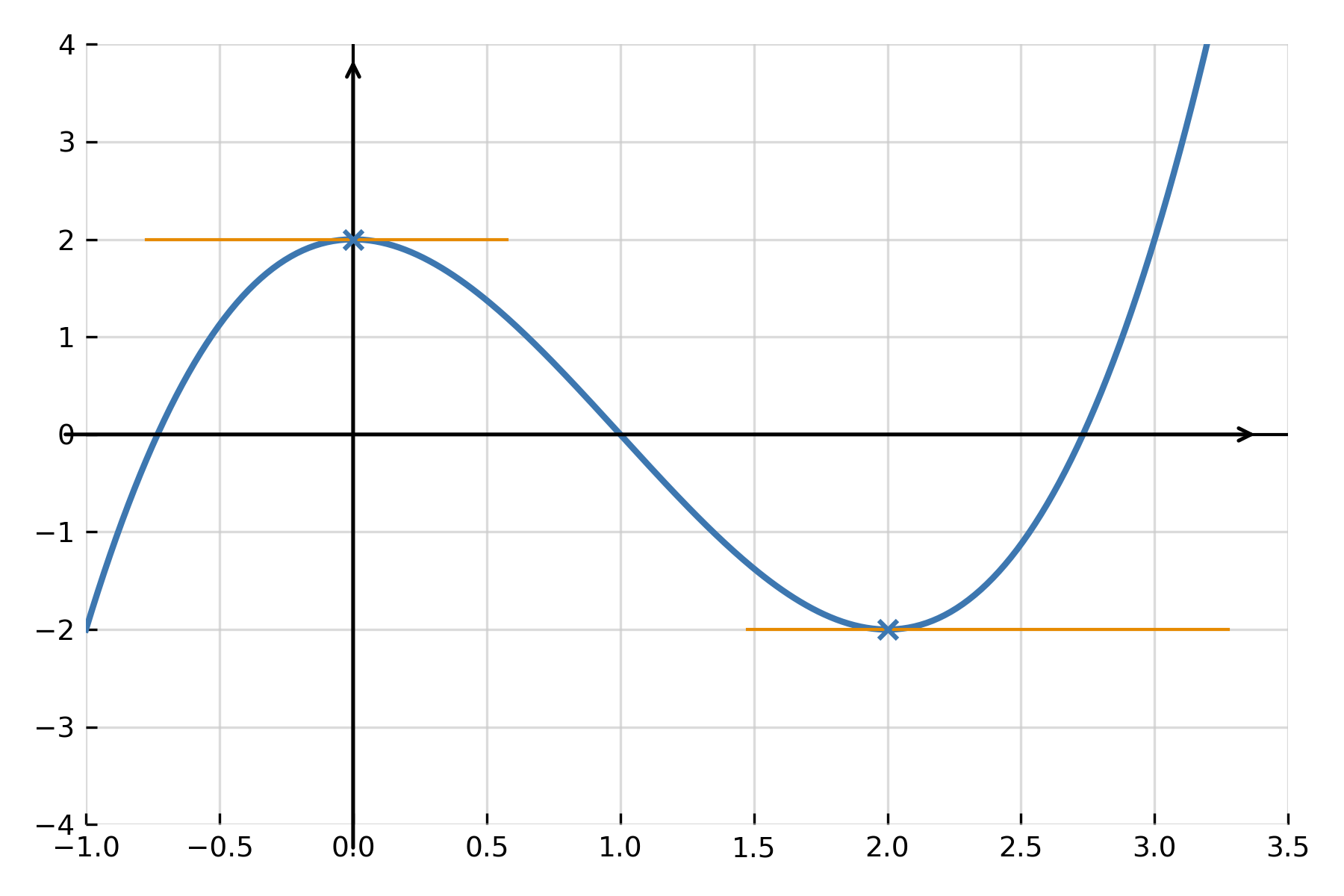
Ekstremum

Ekstremum, maksimum og minimum

Et ekstremum er et punkt, hvor funktionen går fra stigende til faldende (maksimum) eller fra faldende til stigende (minimum). For at afgøre typen undersøger man fortegnet på $ \large f'(x) $ omkring punktet — eller man bruger den anden afledte.

Anden afledte-testen siger:

Hvis $ \large f'(x_0) = 0 $ og $ \large f''(x_0) > 0 $, har funktionen et lokalt minimum i $ \large x_0 $.
Hvis $ \large f'(x_0) = 0 $ og $ \large f''(x_0) < 0 $, har funktionen et lokalt maksimum i $ \large x_0 $.

Eksempel: For $ \large f(x) = x^3 - 3x^2 + 2 $ gælder $ \large f''(x) = 6x - 6 $. Her er $ \large f''(0) = -6 < 0 $ (maksimum) og $ \large f''(2) = 6 > 0 $ (minimum).

Vendepunkter

Et vendepunkt er et sted, hvor grafens krumning ændrer fortegn. Det betyder, at grafen skifter fra at være “bue opad” til “bue nedad” eller omvendt. Et vendepunkt findes, hvor $ \large f''(x) = 0 $ og samtidig ændrer fortegn.

Eksempel: For $ \large f(x) = x^3 - 3x^2 + 2 $ er $ \large f''(x) = 6x - 6 $, som bliver nul ved $ \large x = 1 $. Da fortegnet skifter her, har funktionen et vendepunkt i $ \large x = 1 $.

Optimering

Differentialregning bruges ofte til at løse optimeringsproblemer — altså at finde den største eller mindste værdi af en funktion under givne betingelser. Det kan fx være at maksimere et areal, minimere en omkostning eller finde den hurtigste vej.

Trinvis fremgangsmåde:

Opskriv funktionen, som skal optimeres.
Bestem dens afledte $ \large f'(x) $.
Find de punkter, hvor $ \large f'(x) = 0 $ (stationære punkter).
Brug fortegn eller den anden afledte til at afgøre, om det er maksimum eller minimum.

Eksempel – optimering

Et rektangel skal have et areal, der afhænger af længden $ \large x $:

$$ \large A(x) = x(12 - 2x) = 12x - 2x^2 $$

For at finde det største areal differentieres funktionen:

$$ \large A'(x) = 12 - 4x $$

Sæt $ \large A'(x) = 0 $ → $ \large 12 - 4x = 0 \Rightarrow x = 3 $.

Anden afledte $ \large A''(x) = -4 $ er negativ, så der er tale om et maksimum. Rektanglet har altså størst areal, når længden er $ \large 3 $ og bredden $ \large 12 - 2x = 6 $.

Grafskitse og fortolkning

Ved at kombinere informationen fra $ \large f'(x) $ og $ \large f''(x) $ kan man tegne en nøjagtig graf uden at bruge lommeregner:

$ \large f'(x) $ fortæller, hvor grafen stiger eller falder.
$ \large f''(x) $ fortæller, om grafen er krum opad eller nedad.
$ \large f'(x) = 0 $ giver toppunkter og bundpunkter.
$ \large f''(x) = 0 $ giver vendepunkter.

Dette kaldes en fuldstændig grafanalyse og danner grundlaget for både teoretisk forståelse og praktisk anvendelse af funktioner i naturvidenskab og teknologi.

Opsummering

Den afledte funktion giver mulighed for at analysere og forudsige, hvordan en funktion opfører sig. Med differentialregning kan man finde maksimum og minimum, bestemme intervaller hvor funktionen vokser eller falder, undersøge grafens form og løse optimeringsproblemer. Det gør den til et af de mest anvendelige værktøjer i hele matematikken.