Métodos avanzados

Una vez que se aprenden las reglas básicas de diferenciación, se abre un nuevo mundo de posibilidades. Muchas funciones no pueden escribirse directamente como \( \large y = f(x) \), pero aun así pueden diferenciarse utilizando métodos ampliados. Las tres técnicas más importantes son diferenciación implícita, diferenciación paramétrica y derivadas de funciones inversas.

 

 

Diferenciación implícita

Algunas funciones están dadas por una ecuación donde \( \large x \) y \( \large y \) aparecen juntas, por ejemplo \( \large x^2 + y^2 = 25 \). No se puede aislar \( \large y \) directamente, pero es posible hallar \( \large \frac{dy}{dx} \) diferenciando ambos lados respecto a \( \large x \), recordando que \( \large y \) depende de \( \large x \).

 

Ejemplo:

 

Diferencia \( \large x^2 + y^2 = 25 \) con respecto a \( \large x \):

 

$$ \large 2x + 2y \cdot \frac{dy}{dx} = 0 $$

 

Resuelve para \( \large \frac{dy}{dx} \):

 

$$ \large \frac{dy}{dx} = -\frac{x}{y} $$

 

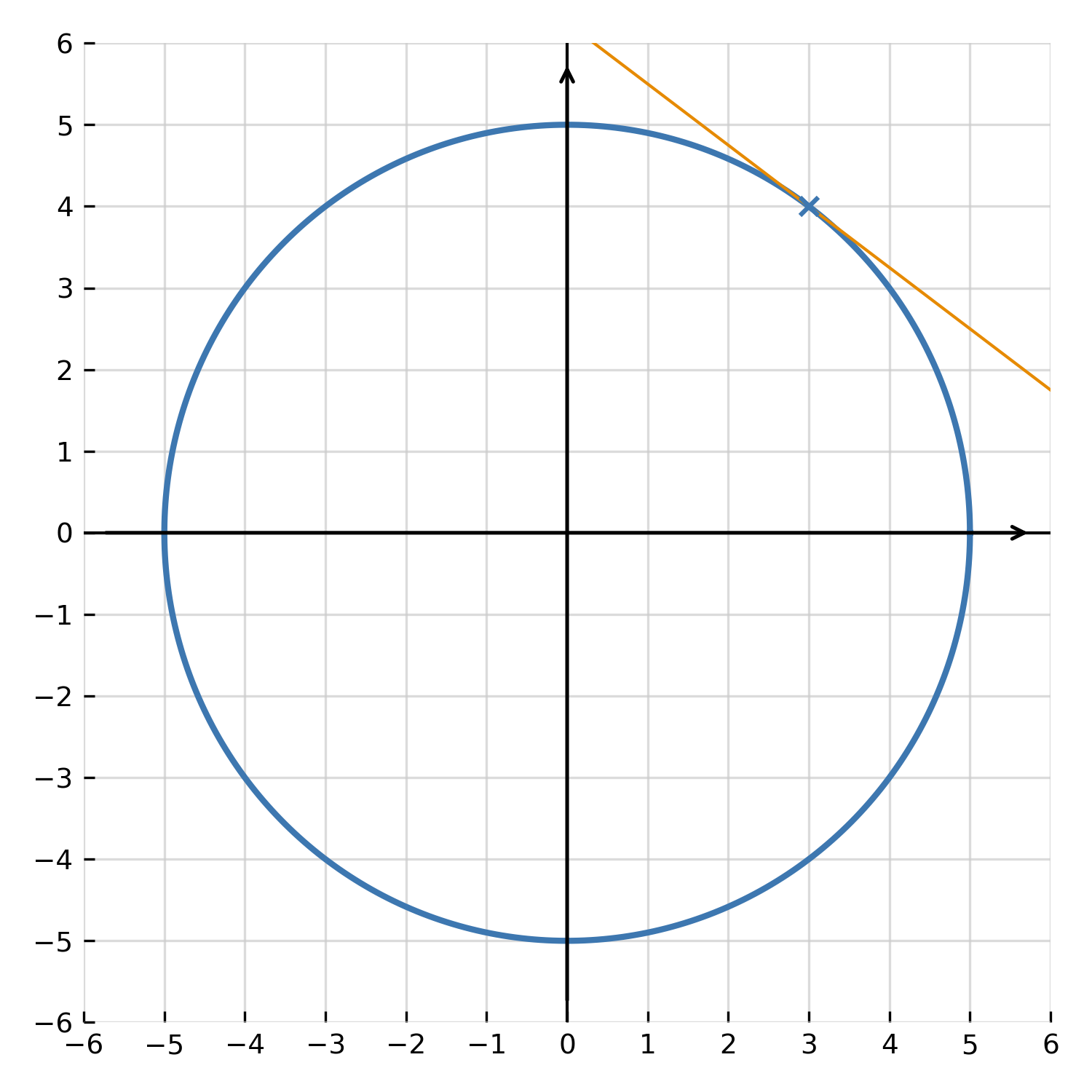
Esta es la pendiente de la tangente al círculo \( \large x^2 + y^2 = 25 \) en cualquier punto. La diferenciación implícita es especialmente útil para curvas que no pueden describirse como funciones en el sentido tradicional, como círculos, elipses e hipérbolas.

 

La regla de la cadena en la práctica

La regla de la cadena se usa cuando una función está compuesta por otra función. Es fundamental en todos los métodos avanzados. Puede pensarse como “un cambio afecta a otro cambio”.

 

Ejemplo:

 

Si \( \large y = \sin(3x^2) \), la función consta de dos capas: \( \large \sin(u) \) donde \( \large u = 3x^2 \). La derivada se obtiene multiplicando las dos tasas de cambio:

 

$$ \large \frac{dy}{dx} = \cos(3x^2) \cdot 6x = 6x \cos(3x^2) $$

 

La regla de la cadena también puede aplicarse varias veces, por ejemplo cuando una función está compuesta por tres o más capas. Se convierte así en una herramienta indispensable en los cálculos avanzados.

 

 

Funciones paramétricas

A veces tanto \( \large x \) como \( \large y \) se dan como funciones de una tercera variable, normalmente llamada \( \large t \) (el parámetro). Esto ocurre, por ejemplo, en cinemática, donde una partícula se mueve en el espacio y se conoce su posición como función del tiempo.

 

Si \( \large x = x(t) \) y \( \large y = y(t) \), se puede hallar \( \large \frac{dy}{dx} \) combinando las dos derivadas respecto a \( \large t \):

 

$$ \large \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} $$

 

Ejemplo:

 

Si \( \large x = t^2 \) y \( \large y = 3t + 1 \), entonces

$$ \large \frac{dx}{dt} = 2t \qquad \text{y} \qquad \frac{dy}{dt} = 3 $$

 

Por lo tanto,

$$ \large \frac{dy}{dx} = \frac{3}{2t} $$

 

Esta expresión muestra la pendiente de la curva en el punto correspondiente al parámetro \( \large t \).

 

 

Funciones inversas

Si una función tiene una inversa, también es posible encontrar la derivada de la inversa sin determinarla explícitamente. Sea \( \large y = f(x) \) una función derivable con inversa \( \large x = f^{-1}(y) \). Se cumple la relación:

 

$$ \large \frac{dy}{dx} = f'(x) \quad \Rightarrow \quad \frac{dx}{dy} = \frac{1}{f'(x)} $$

 

En otras palabras, la derivada de la función inversa es el recíproco de la derivada de la función original.

 

Ejemplo:

 

Si \( \large f(x) = e^x \), entonces \( \large f^{-1}(x) = \ln(x) \). Como \( \large f'(x) = e^x \), se obtiene:

 

$$ \large (\ln x)' = \frac{1}{e^x} = \frac{1}{x} $$

 

Esto coincide con la derivada conocida del logaritmo y demuestra el principio en la práctica.

 

 

Métodos combinados

A menudo se encuentran funciones en las que deben usarse varias de estas técnicas juntas, por ejemplo, una ecuación implícita que involucra un parámetro o una función compuesta que debe invertirse. El matemático experimentado aprende a combinar las reglas naturalmente:

 

$$ \large \frac{dy}{dx} = \frac{dy}{dt} \cdot \frac{dt}{dx} $$

 

En realidad, esto es solo una versión extendida de la regla de la cadena, que permite cambiar entre variables según sea necesario.

 

 

Resumen

Los métodos ampliados permiten diferenciar funciones que no pueden escribirse en forma simple. La diferenciación implícita se usa para relaciones entre \( \large x \) y \( \large y \), la diferenciación paramétrica se aplica cuando ambas dependen de un parámetro, y la regla de las funciones inversas permite hallar derivadas de logaritmos y funciones trigonométricas inversas. Estas herramientas amplían el alcance del cálculo diferencial y forman la base de temas más avanzados en análisis.