Linealización y aproximación
El cálculo diferencial permite comprender y aproximar funciones localmente. Cuando una función es suave y derivable, puede reemplazarse por una línea recta en una pequeña región alrededor de un punto – es decir, la línea tangente. Este método se llama linealización y se utiliza para encontrar aproximaciones rápidas cuando los cálculos exactos son difíciles o innecesarios.
Idea de la linealización
Cerca de un punto \( \large x_0 \), una función derivable \( \large f(x) \) se comporta casi como su tangente. Si se conoce la función y su derivada en ese punto, se puede describir todo su comportamiento local mediante una función lineal, que es fácil de calcular.
La aproximación lineal (la ecuación de la tangente) tiene la forma:
$$ \large f(x) \approx f(x_0) + f'(x_0) \cdot (x - x_0) $$
Esta expresión indica que el valor de la función en un punto cercano a \( \large x_0 \) puede aproximarse por el valor en \( \large x_0 \) más el cambio dado por la pendiente \( \large f'(x_0) \). Cuanto más cerca esté \( \large x \) de \( \large x_0 \), mejor funciona la aproximación.
Comprensión gráfica
La línea tangente “toca” la gráfica de \( \large f(x) \) en un solo punto y sigue su dirección allí. Para pequeños cambios en \( \large x \), la función y la tangente casi coinciden. La linealización significa, por tanto, reemplazar una curva por su línea recta local. Esto simplifica mucho los cálculos sin perder precisión en esa región.
Ejemplo 1: Linealización de una función cuadrática
Encontrar la aproximación lineal de \( \large f(x) = x^2 \) alrededor del punto \( \large x_0 = 2 \).
Se tiene \( \large f(2) = 4 \) y \( \large f'(x) = 2x \), por lo que \( \large f'(2) = 4 \). Entonces:
$$ \large f(x) \approx 4 + 4(x - 2) = 4x - 4 $$
Cuando \( \large x \) está cerca de 2, \( \large 4x - 4 \) es una buena aproximación de \( \large x^2 \). Por ejemplo, \( \large f(2.1) \approx 4.4 \), mientras que el valor exacto es \( \large 2.1^2 = 4.41 \).
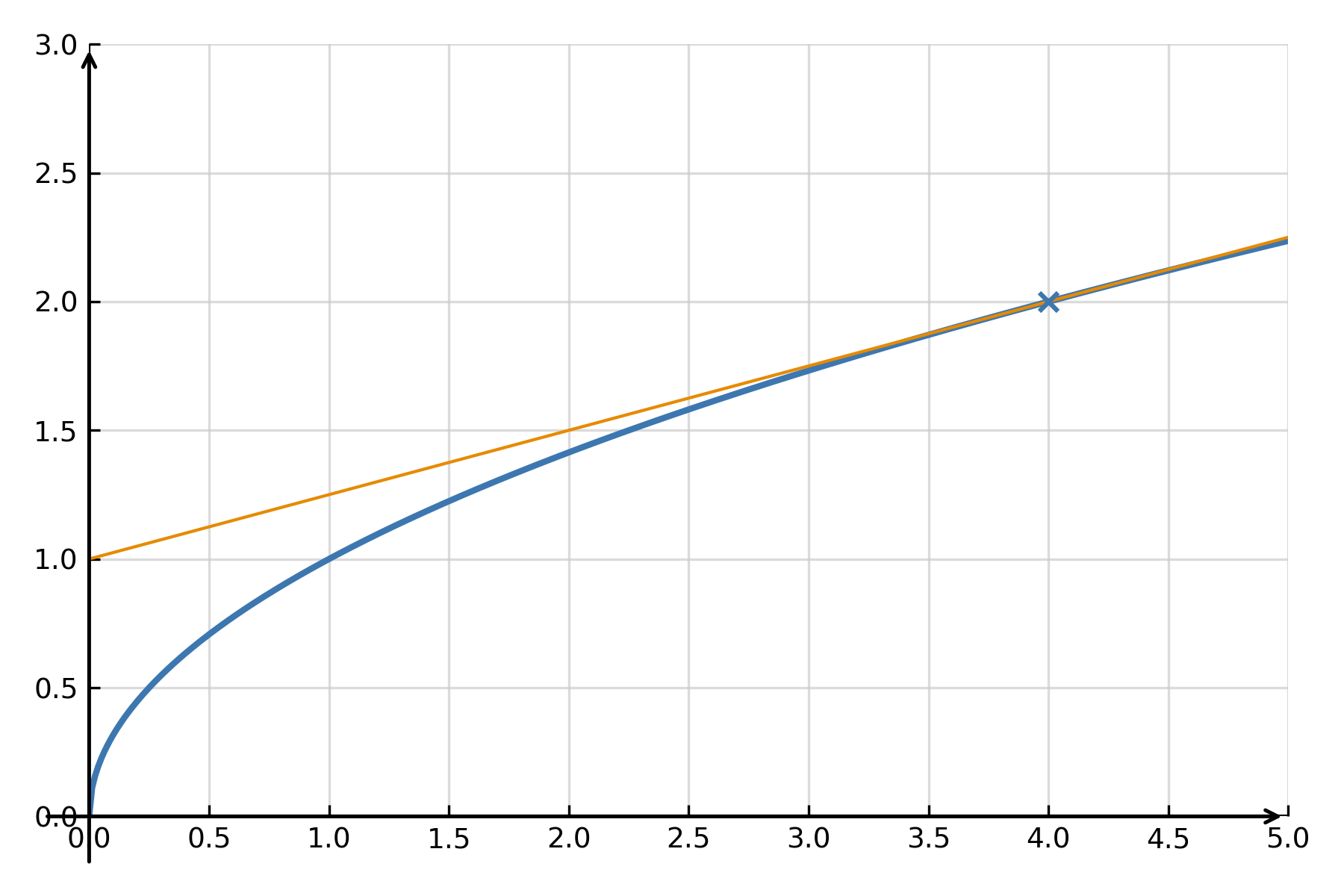
Ejemplo 2: Aproximación de una raíz cuadrada
La linealización puede usarse para aproximar raíces cuadradas sin calculadora. Por ejemplo, \( \large \sqrt{4.1} \) puede hallarse linealizando la función \( \large f(x) = \sqrt{x} \) alrededor de \( \large x_0 = 4 \).
Aquí, \( \large f(4) = 2 \) y \( \large f'(x) = \frac{1}{2\sqrt{x}} \), por lo que \( \large f'(4) = \frac{1}{4} \).
$$ \large f(x) \approx 2 + \frac{1}{4}(x - 4) $$
Para \( \large x = 4.1 \): \( \large f(4.1) \approx 2 + \frac{1}{4} \cdot 0.1 = 2.025 \), mientras que el valor exacto es \( \large 2.0248 \). La aproximación tangente da un resultado con un error casi nulo.
Error y precisión
Cuanto más cerca esté \( \large x \) de \( \large x_0 \), mejor funciona la aproximación. Si uno se aleja, la línea tangente empieza a desviarse de la curva original, porque los cambios de orden superior (curvatura) se vuelven importantes. Esto puede corregirse incluyendo más términos en un desarrollo de Taylor.
En primera orden, la linealización corresponde a la primera parte de la serie de Taylor:
$$ \large f(x) = f(x_0) + f'(x_0)(x - x_0) + \frac{f''(x_0)}{2!}(x - x_0)^2 + \dots $$
Al tomar solo el primer término después de \( \large f(x_0) \), se obtiene precisamente la aproximación tangente. Por eso el método también se llama aproximación de Taylor de primer orden.
Ejemplo 3: Interpretación física
En física, la linealización se utiliza para describir movimientos o procesos en intervalos de tiempo cortos. Si \( \large s(t) \) describe una posición, la aproximación lineal
$$ \large s(t) \approx s(t_0) + v(t_0) \cdot (t - t_0) $$
puede interpretarse como: “la nueva posición es la anterior más la velocidad por el tiempo”. Aquí la velocidad \( \large v(t_0) = s'(t_0) \) desempeña el mismo papel que la pendiente de la tangente en matemáticas.
Resumen
La linealización permite reemplazar una función por un modelo lineal simple alrededor de un punto dado. La línea tangente actúa como una aproximación local rápida y suficientemente precisa. El método constituye la base de muchos procedimientos numéricos y del desarrollo de Taylor, que amplía la idea a aproximaciones más exactas.