La función derivada
La función derivada indica qué tan rápido cambia otra función. Si \( \large f(x) \) representa una magnitud, la derivada \( \large f'(x) \) muestra cuánto cambia dicha magnitud cuando \( \large x \) varía ligeramente. De esta manera, el cálculo diferencial se convierte en una herramienta precisa para medir el cambio.
De la secante a la tangente
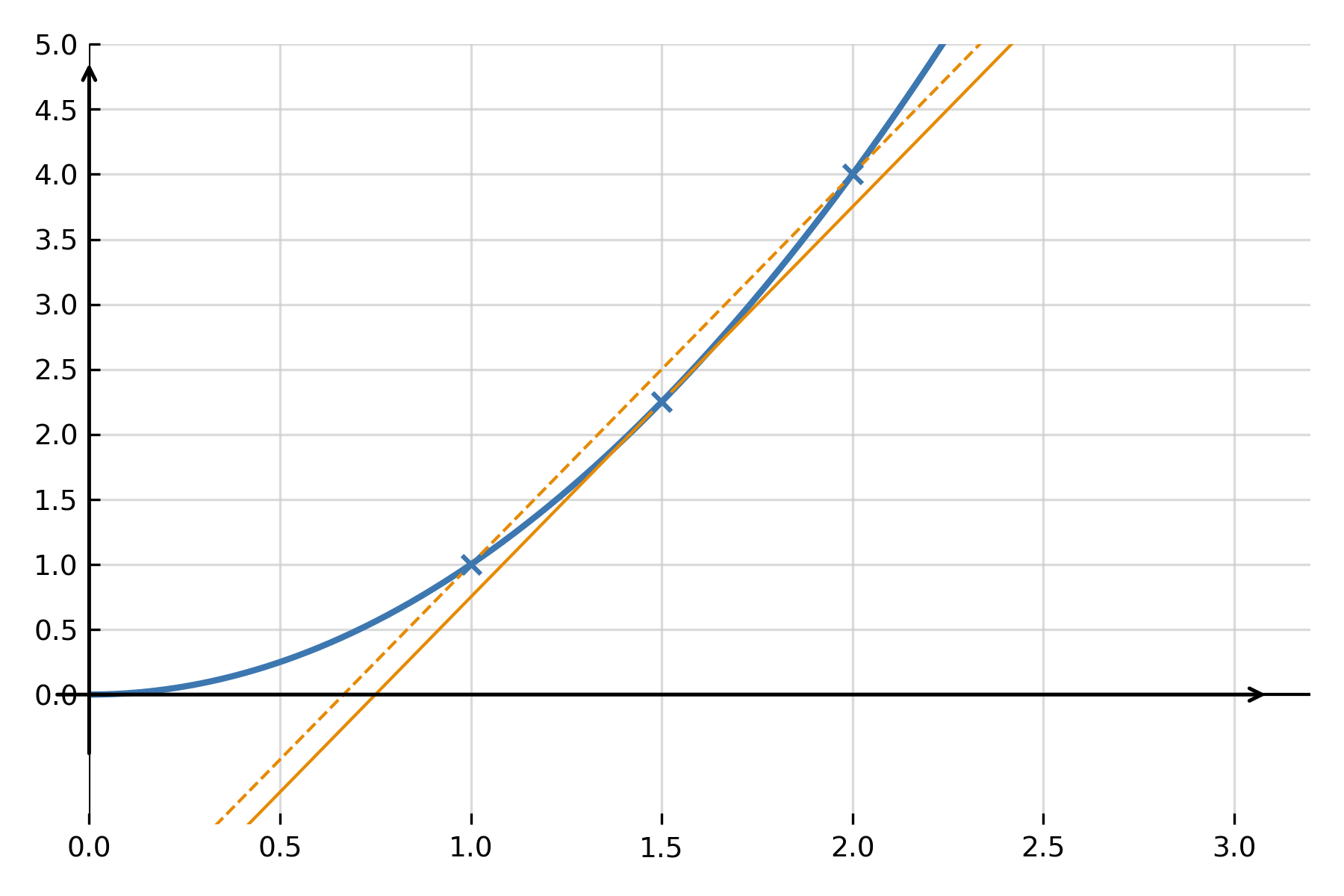
Para entender qué significa “derivar”, se comienza con la pendiente de una secante. Una secante es la línea recta que une dos puntos de la gráfica de \( \large f(x) \). La pendiente de la secante muestra cuánto aumenta o disminuye la función en promedio entre los dos puntos.
$$ \large a_{\text{secante}} = \frac{f(x+h) - f(x)}{h} $$
Si se eligen los puntos cada vez más cerca uno del otro, de modo que \( \large h \) sea muy pequeño, la secante se aproxima a una línea que toca la gráfica en un solo punto — la tangente. La pendiente de esta tangente se llama la tasa de cambio instantánea. Este es precisamente el valor que nos da la función derivada.
Definición mediante el límite
La definición precisa de la función derivada es:
$$ \large f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} $$
Aquí, la fracción mide cuánto cambia \( \large f(x) \) cuando \( \large x \) cambia en una pequeña cantidad \( \large h \). Cuando \( \large h \) tiende a cero, se obtiene el cambio en ese punto exacto — la pendiente de la tangente. El límite solo existe si la función es lo suficientemente suave en ese punto, es decir, si no tiene saltos, puntas o quiebros.
Notación y lectura
Existen varias formas de escribir la derivada:
$$ \large f'(x) \quad \text{o} \quad \frac{dy}{dx} \quad \text{o} \quad Df(x) $$
Las tres significan lo mismo: cuánto cambia \( \large y \) cuando \( \large x \) cambia. En física, por ejemplo, \( \large \frac{dy}{dt} \) se lee como “cambio en la distancia sobre cambio en el tiempo”, es decir, velocidad.
Comprensión gráfica
La función derivada da una nueva función que, en cada punto, indica la pendiente de la gráfica de \( \large f(x) \). Donde la gráfica sube, la derivada es positiva; donde baja, es negativa; y donde la gráfica tiene una tangente horizontal, la derivada es cero.
Un punto donde \( \large f'(x) = 0 \) se llama un punto estacionario. Dichos puntos desempeñan un papel importante más adelante al buscar los máximos y mínimos de las funciones.
Interpretación física
En muchos contextos, la derivada representa una magnitud física. Si \( \large f(x) \) describe una posición como función del tiempo, entonces \( \large f'(x) \) es la velocidad — qué tan rápido se mueve. Si se deriva una vez más, se obtiene la aceleración \( \large f''(x) \), que muestra qué tan rápido cambia la velocidad.
Ejemplos
1. Ejemplo – función cuadrática
Para \( \large f(x) = x^2 \), la derivada puede calcularse directamente a partir de la definición:
$$ \large f'(x) = \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} = \lim_{h \to 0} \frac{2xh + h^2}{h} = 2x $$
La función derivada es \( \large f'(x) = 2x \). La pendiente depende, por tanto, del punto en la gráfica. En \( \large x = 3 \), la pendiente es \( \large f'(3) = 6 \).
2. Ejemplo – función lineal
Para \( \large f(x) = 5x + 2 \), la gráfica ya es una línea recta. Su pendiente es constante, por lo que la derivada es:
$$ \large f'(x) = 5 $$
Aquí, la función aumenta siempre 5 unidades cuando \( \large x \) aumenta en 1. Esto muestra que el cálculo diferencial generaliza la idea conocida de pendiente de las líneas rectas a todas las funciones suaves.
3. Ejemplo – interpretación física
Si \( \large s(t) = t^2 \) describe la distancia recorrida por un coche en metros como función del tiempo \( \large t \) en segundos, entonces la velocidad es \( \large v(t) = s'(t) = 2t \). Después de 4 segundos, el coche se mueve a \( \large v(4) = 8 \) m/s. La derivada proporciona aquí una medida directa de la velocidad del movimiento.
Mini reglas
Al calcular derivadas de funciones comunes, se aplican algunas reglas simples:
$$ \large (k)' = 0 \qquad (x^n)' = n \cdot x^{n-1} \qquad (k \cdot f(x))' = k \cdot f'(x) $$
Estas forman la base de las reglas generales de derivación tratadas en la siguiente sección. Con ellas, se pueden derivar incluso funciones bastante complejas sin volver a la definición del límite.
Resumen
La función derivada expresa qué tan rápido cambia una función en cada punto. Puede entenderse como la pendiente de la tangente, como una medida de la tasa de cambio o como una herramienta matemática para describir movimiento y crecimiento. Desempeña un papel central en casi todas las áreas de las matemáticas, la física y la economía.