Aplicaciones del cálculo diferencial

El cálculo diferencial no solo se utiliza para calcular pendientes. También proporciona una comprensión más profunda de cómo se comportan las funciones. Al estudiar la derivada, se puede determinar dónde una función crece o decrece, encontrar su máximo y mínimo, y analizar su forma gráfica. El método se aplica en todo, desde la física y la economía hasta la biología y la ingeniería.

Monotonía: dónde la función crece y decrece

La función derivada $ \large f'(x) $ indica si $ \large f(x) $ es creciente o decreciente en un intervalo dado:

Si $ \large f'(x) > 0 $, la función es creciente.
Si $ \large f'(x) < 0 $, la función es decreciente.
Si $ \large f'(x) = 0 $, la función tiene un punto estacionario.

Un punto estacionario es un lugar donde la pendiente de la tangente es cero. Puede ser un máximo local, un mínimo local o un punto de inflexión.

Ejemplo: Análisis de una función

Analiza la función $ \large f(x) = x^3 - 3x^2 + 2 $.

Primero, se calcula la derivada:

$$ \large f'(x) = 3x^2 - 6x = 3x(x - 2) $$

La derivada es cero para $ \large x = 0 $ y $ \large x = 2 $. Se analiza el signo de $ \large f'(x) $ en los intervalos:

Para $ \large x < 0 $: $ \large f'(x) > 0 $ → creciente
Para $ \large 0 < x < 2 $: $ \large f'(x) < 0 $ → decreciente
Para $ \large x > 2 $: $ \large f'(x) > 0 $ → creciente

Por lo tanto, la función tiene un máximo local en $ \large x = 0 $ y un mínimo local en $ \large x = 2 $. Este método se llama tabla de signos y se utiliza para determinar dónde la función aumenta o disminuye.

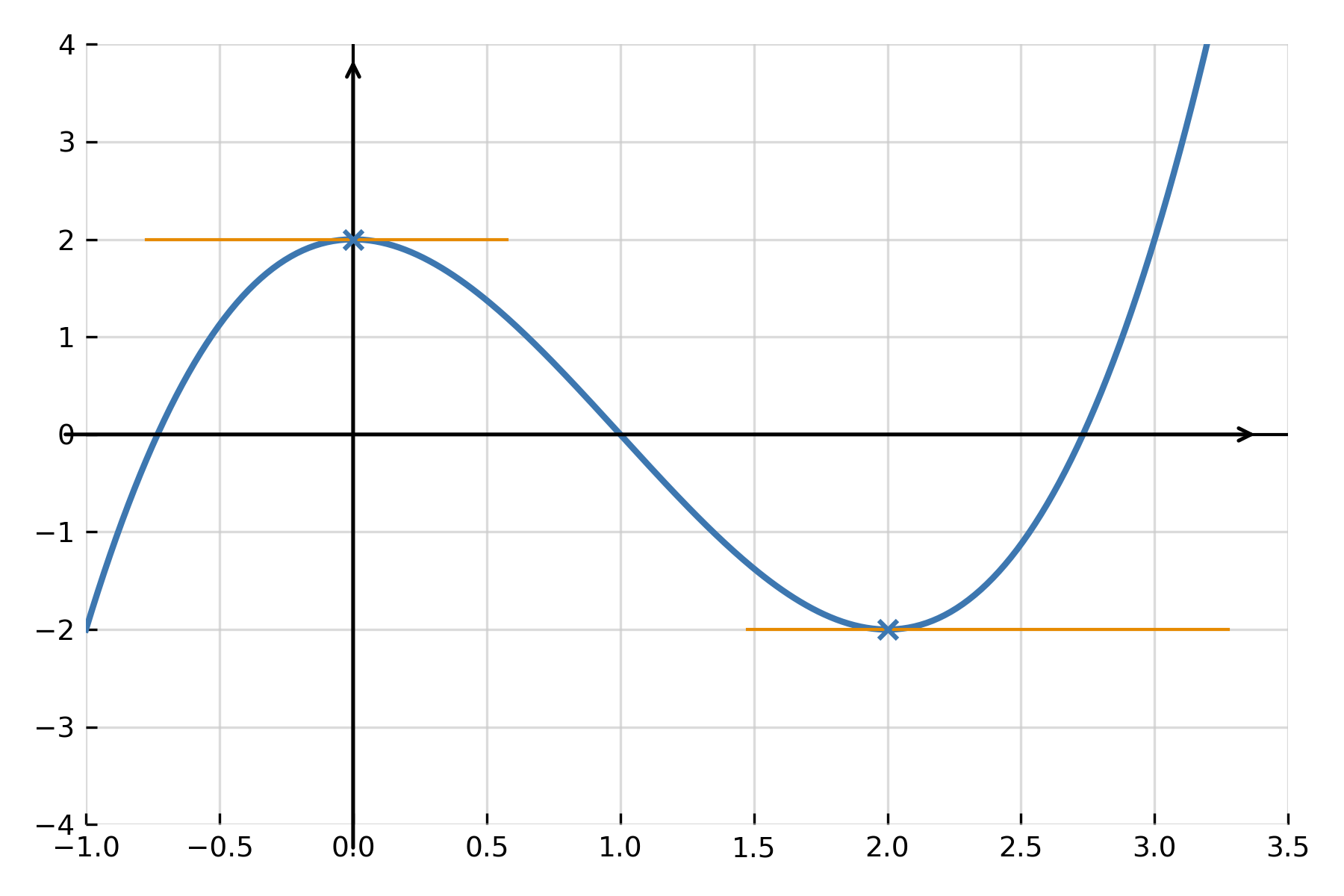
Extremo

Extremos, máximo y mínimo

Un extremo es un punto donde la función pasa de creciente a decreciente (máximo) o de decreciente a creciente (mínimo). Para determinar el tipo, se examina el signo de $ \large f'(x) $ alrededor del punto — o se utiliza la segunda derivada.

La prueba de la segunda derivada establece:

Si $ \large f'(x_0) = 0 $ y $ \large f''(x_0) > 0 $, la función tiene un mínimo local en $ \large x_0 $.
Si $ \large f'(x_0) = 0 $ y $ \large f''(x_0) < 0 $, la función tiene un máximo local en $ \large x_0 $.

Ejemplo: Para $ \large f(x) = x^3 - 3x^2 + 2 $, se cumple $ \large f''(x) = 6x - 6 $. Aquí $ \large f''(0) = -6 < 0 $ (máximo) y $ \large f''(2) = 6 > 0 $ (mínimo).

Puntos de inflexión

Un punto de inflexión es un lugar donde la curvatura de la gráfica cambia de signo. Esto significa que la gráfica pasa de ser “cóncava hacia arriba” a “cóncava hacia abajo” o viceversa. Un punto de inflexión se encuentra donde $ \large f''(x) = 0 $ y el signo cambia.

Ejemplo: Para $ \large f(x) = x^3 - 3x^2 + 2 $, $ \large f''(x) = 6x - 6 $, que se hace cero en $ \large x = 1 $. Dado que el signo cambia, la función tiene un punto de inflexión en $ \large x = 1 $.

Optimización

El cálculo diferencial se utiliza a menudo para resolver problemas de optimización — es decir, encontrar el valor más grande o más pequeño de una función bajo ciertas condiciones. Puede tratarse, por ejemplo, de maximizar un área, minimizar un coste o encontrar el camino más rápido.

Procedimiento paso a paso:

Escribe la función que se va a optimizar.
Encuentra su derivada $ \large f'(x) $.
Encuentra los puntos donde $ \large f'(x) = 0 $ (puntos estacionarios).
Utiliza el signo o la segunda derivada para determinar si es un máximo o un mínimo.

Ejemplo – optimización

Un rectángulo tiene un área que depende de su longitud $ \large x $:

$$ \large A(x) = x(12 - 2x) = 12x - 2x^2 $$

Para encontrar el área máxima, se deriva la función:

$$ \large A'(x) = 12 - 4x $$

Se establece $ \large A'(x) = 0 $ → $ \large 12 - 4x = 0 \Rightarrow x = 3 $.

La segunda derivada $ \large A''(x) = -4 $ es negativa, por lo que se trata de un máximo. El rectángulo tiene el área máxima cuando la longitud es $ \large 3 $ y el ancho $ \large 12 - 2x = 6 $.

Boceto gráfico e interpretación

Combinando la información de $ \large f'(x) $ y $ \large f''(x) $, se puede dibujar una gráfica precisa sin utilizar calculadora:

$ \large f'(x) $ muestra dónde la gráfica sube o baja.
$ \large f''(x) $ indica si la gráfica es cóncava hacia arriba o hacia abajo.
$ \large f'(x) = 0 $ da los puntos máximos y mínimos.
$ \large f''(x) = 0 $ da los puntos de inflexión.

Esto se llama un análisis gráfico completo y constituye la base tanto para la comprensión teórica como para la aplicación práctica de las funciones en la ciencia y la tecnología.

Resumen

La derivada permite analizar y predecir cómo se comporta una función. Con el cálculo diferencial, se pueden encontrar los máximos y mínimos, determinar los intervalos donde la función crece o decrece, estudiar la forma de la gráfica y resolver problemas de optimización. Esto la convierte en una de las herramientas más útiles de toda la matemática.