Skalarprodukt und Winkel

Das Skalarprodukt ist eine Möglichkeit, zwei Vektoren zu kombinieren, die eine Zahl ergibt. Es wird unter anderem verwendet, um den Winkel zwischen zwei Vektoren zu bestimmen und um festzustellen, ob sie senkrecht sind.

 

Definition

Für zwei Vektoren \( \large \mathbf{u} = (x_1,y_1) \) und \( \large \mathbf{v} = (x_2,y_2) \) gilt:

 

$$ \large \mathbf{u} \cdot \mathbf{v} = x_1 \cdot x_2 + y_1 \cdot y_2 $$

 

Außerdem kann das Skalarprodukt geschrieben werden als:

 

$$ \large \mathbf{u} \cdot \mathbf{v} = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \cos(\theta) $$

 

wobei \( \large \theta \) der Winkel zwischen den Vektoren ist.

 

 

Beispiele

Beispiel 1:

 

$$ \large \mathbf{u} = (1,0), \; \mathbf{v} = (0,1) $$

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 0 + 0 \cdot 1 = 0 $$

 

Die Vektoren sind orthogonal (senkrecht), und der Winkel beträgt \( \large 90^\circ \).

 

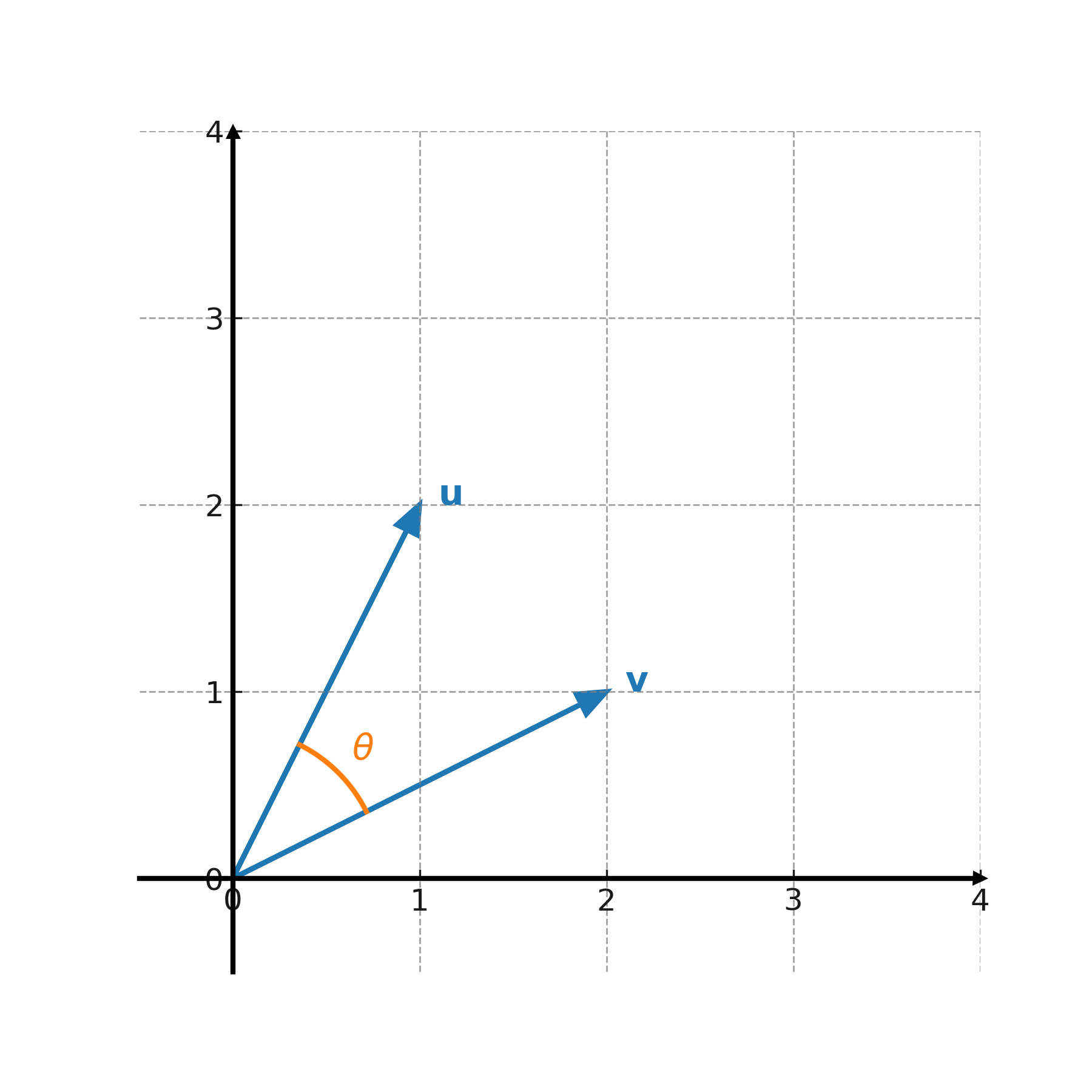
Beispiel 2:

 

$$ \large \mathbf{u} = (1,2), \; \mathbf{v} = (2,1) $$

$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 2 + 2 \cdot 1 = 4 $$

 

Die Längen sind \( \large |\mathbf{u}| = \sqrt{5}, \; |\mathbf{v}| = \sqrt{5} \). Damit:

 

$$ \large \cos(\theta) = \frac{4}{\sqrt{5} \cdot \sqrt{5}} = \frac{4}{5} $$

 

Der Winkel ist daher:

 

$$ \large \theta = \cos^{-1}\left(\frac{4}{5}\right) \approx 36,9^\circ $$

 

 

Geometrische Interpretation

Das Skalarprodukt misst, wie viel von einem Vektor in die gleiche Richtung wie der andere zeigt. Ist der Winkel spitz, ist das Produkt positiv. Ist der Winkel stumpf, ist das Produkt negativ. Ist der Winkel recht, ist das Produkt null.

 

 

Anwendung

Das Skalarprodukt wird in Mathematik und Physik verwendet, um Winkel zu bestimmen und um festzustellen, ob Vektoren senkrecht sind. In der Physik wird es auch verwendet, um den Anteil einer Kraft zu berechnen, der in eine bestimmte Richtung wirkt.