Projektionen

Die Projektion eines Vektors auf einen anderen beschreibt, wie viel von einem Vektor in die Richtung des anderen zeigt. Es entspricht dem Betrachten des Vektors als Schatten, der auf den anderen Vektor fällt.

 

Definition

Die Projektion von \( \large \mathbf{u} \) auf \( \large \mathbf{v} \) ist gegeben durch:

 

$$ \large \text{proj}_{\mathbf{v}}(\mathbf{u}) = \frac{\mathbf{u} \cdot \mathbf{v}}{|\mathbf{v}|^2} \cdot \mathbf{v} $$

 

Beispiel

Wir nehmen \( \large \mathbf{u} = (3,4) \) und \( \large \mathbf{v} = (4,0) \).

 

Zuerst wird das Skalarprodukt berechnet:

 

$$ \large \mathbf{u} \cdot \mathbf{v} = 3 \cdot 4 + 4 \cdot 0 = 12 $$

 

Die Länge von \( \large \mathbf{v} \) ist:

 

$$ \large |\mathbf{v}|^2 = 4^2 + 0^2 = 16 $$

 

Die Projektion ist daher:

 

$$ \large \text{proj}_{\mathbf{v}}(\mathbf{u}) = \frac{12}{16} \cdot (4,0) = (3,0) $$

 

Geometrische Interpretation

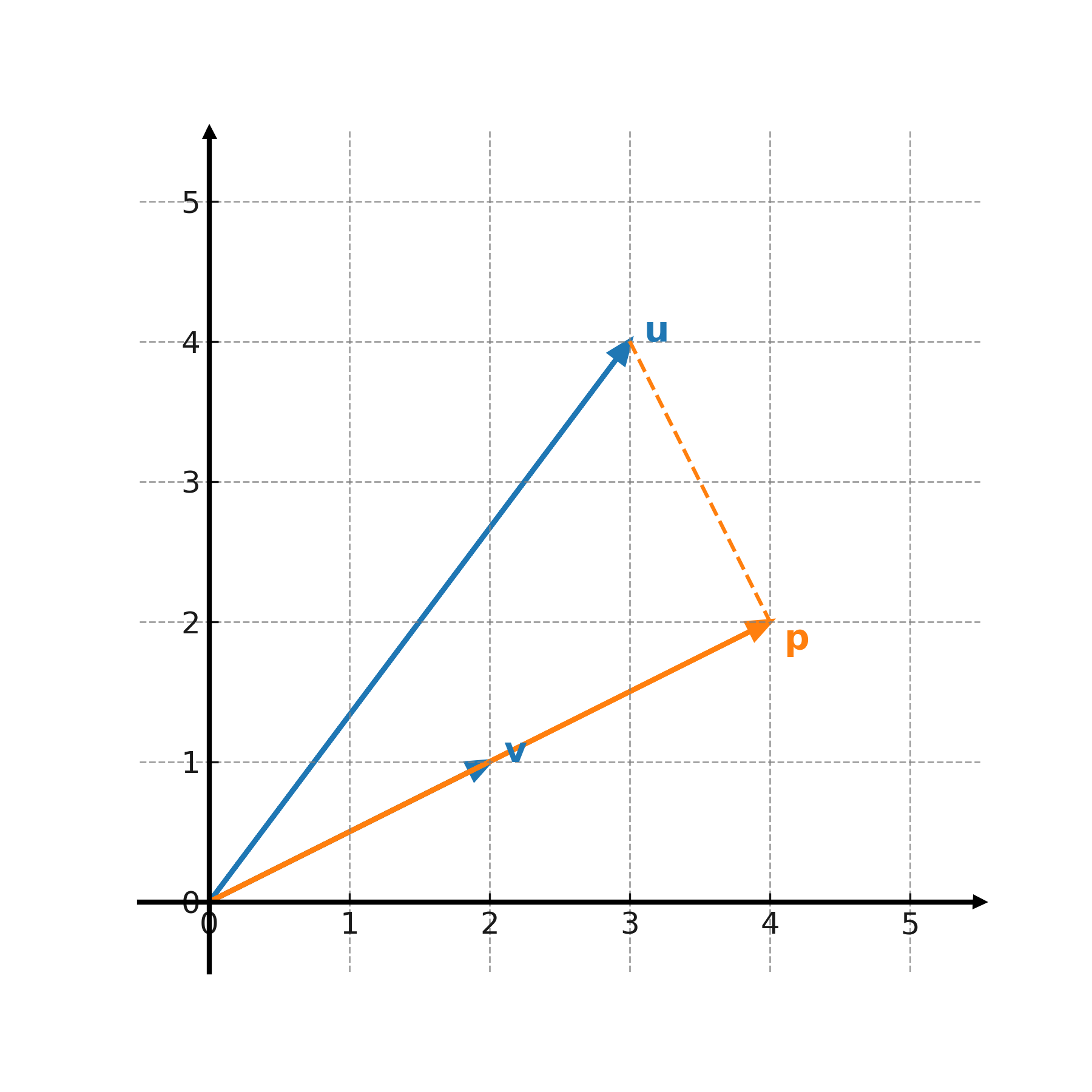
Die Projektion ist der Vektor, der auf \( \large \mathbf{v} \) liegt und den Teil von \( \large \mathbf{u} \) darstellt, der in die gleiche Richtung zeigt. Man kann es sich vorstellen wie einen Schatten, den \( \large \mathbf{u} \) auf die Gerade durch \( \large \mathbf{v} \) wirft.

 

Hinweis: Die Differenz \( \large \mathbf{u} - \text{proj}_{\mathbf{v}}(\mathbf{u}) \) steht immer senkrecht auf \( \large \mathbf{v} \). Somit kann ein Vektor in einen Teil entlang \( \mathbf{v} \) und einen Teil senkrecht zu \( \mathbf{v} \) zerlegt werden.

 

Wenn der Winkel zwischen \( \mathbf{u} \) und \( \mathbf{v} \) größer als \( 90^\circ \) ist, zeigt die Projektion rückwärts entlang \( \mathbf{v} \), was einen negativen Skalarwert vor \( \mathbf{v} \) ergibt.

 

 

Anwendung

Projektionen werden häufig in der Physik verwendet, um den Anteil einer Kraft zu berechnen, der in eine bestimmte Richtung wirkt, und in der Mathematik, um Komponenten von Vektoren entlang gegebener Achsen zu finden.