Addition und Subtraktion

Wenn man mit Vektoren in der Ebene arbeitet, kann man sie addieren oder subtrahieren. Dies geschieht durch die Kombination der Koordinaten jedes Vektors.

 

Definition

Für zwei Vektoren \( \large \mathbf{u} = (x_1,y_1) \) und \( \large \mathbf{v} = (x_2,y_2) \) gilt:

 

$$ \large \mathbf{u} + \mathbf{v} = (x_1 + x_2,\; y_1 + y_2) $$

 

$$ \large \mathbf{u} - \mathbf{v} = (x_1 - x_2,\; y_1 - y_2) $$

 

 

Beispiel

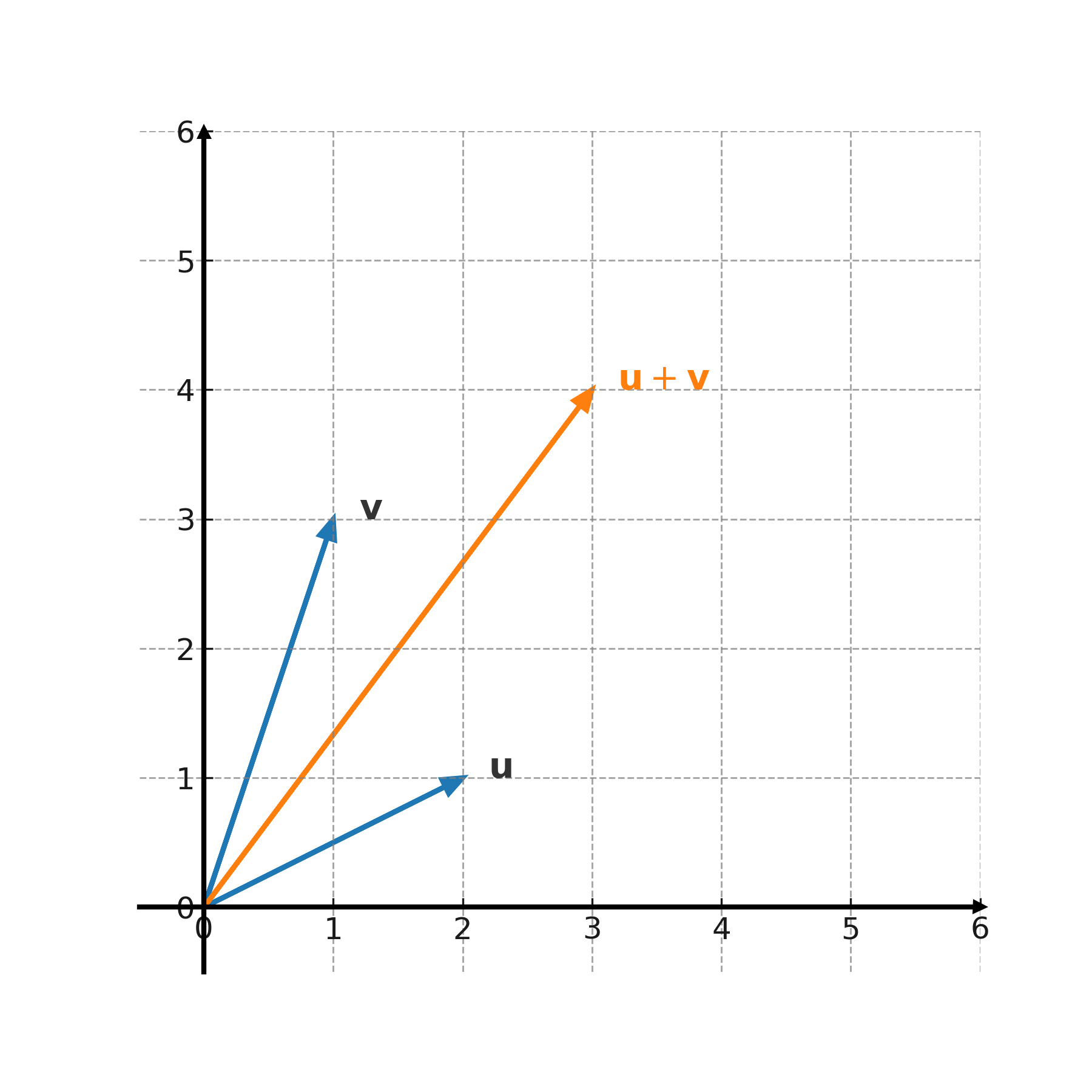
Wir wollen die Summe und die Differenz der Vektoren \( \large \mathbf{u} = (2,1) \) und \( \large \mathbf{v} = (1,3) \) berechnen.

 

Die Summe ist:

 

$$ \large (2,1) + (1,3) = (2+1,\; 1+3) = (3,4) $$

 

 

Die Differenz ist:

 

$$ \large (2,1) - (1,3) = (2-1,\; 1-3) = (1,-2) $$

 

 

Geometrische Interpretation

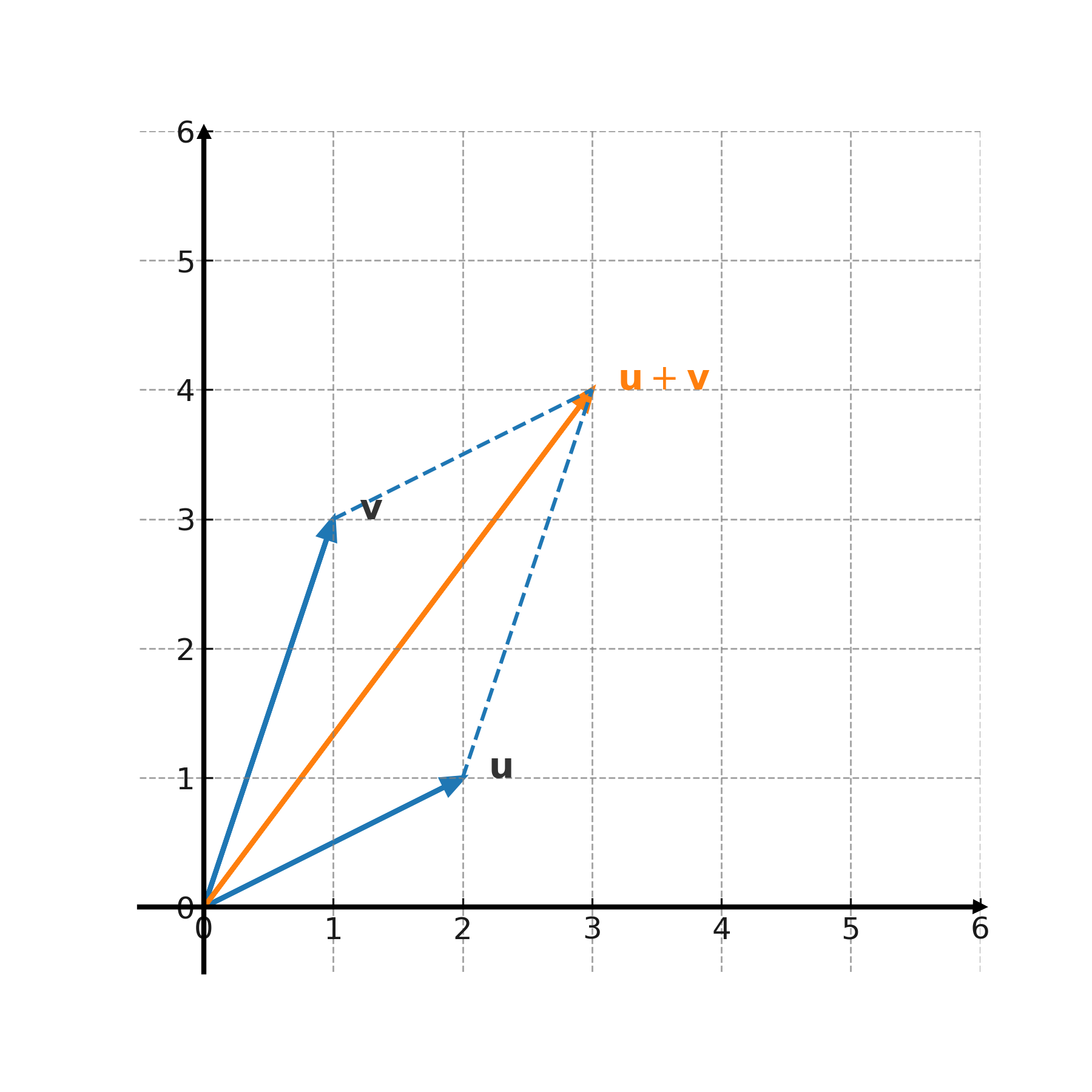
Die Addition kann graphisch mit der Parallelogrammmethode dargestellt werden: Man legt die Vektoren Schwanz an Schwanz und zeichnet zwei Kopien, sodass ein Parallelogramm entsteht. Die Diagonale stellt die Summe dar.

 

 

Die Subtraktion kann als Addition des entgegengesetzten Vektors gesehen werden. Zum Beispiel gilt \( \large \mathbf{u} - \mathbf{v} = \mathbf{u} + (-\mathbf{v}) \).

 

 

Anwendung

In der Physik wird die Vektoraddition verwendet, um die Gesamtkraft auf einen Körper zu bestimmen. Wenn eine Kiste in eine Richtung von einer Kraft und in eine andere Richtung von einer weiteren Kraft gezogen wird, ergibt sich die resultierende Bewegung aus der Summe der beiden Kraftvektoren.