Multiplikation mit einem Skalar

Wenn man einen Vektor mit einer Zahl multipliziert, ändert sich seine Länge, aber die Richtung bleibt erhalten, wenn die Zahl positiv ist. Ist die Zahl negativ, wird der Vektor in die entgegengesetzte Richtung umgekehrt.

 

Definition

Für einen Vektor \( \large \mathbf{v} = (x,y) \) und eine Zahl \( \large k \) gilt:

 

$$ \large k \cdot (x,y) = (k \cdot x,\; k \cdot y) $$

 

Beispiele

Wir betrachten den Vektor \( \large \mathbf{v} = (2,1) \).

 

Wenn \( \large k = 2 \):

$$ \large 2 \cdot (2,1) = (4,2) $$

 

Wenn \( \large k = -1 \):

$$ \large -1 \cdot (2,1) = (-2,-1) $$

 

Wenn \( \large k = \frac{1}{2} \):

$$ \large \frac{1}{2} \cdot (2,1) = (1,\; \frac{1}{2}) $$

 

Wenn \( \large k = 0 \):

$$ \large 0 \cdot (2,1) = (0,0) $$

 

Geometrische Interpretation

Die Multiplikation mit einer Zahl streckt oder verkleinert den Vektor. Bei positiven Zahlen bleibt die Richtung erhalten; bei negativen Zahlen wird die Richtung umgekehrt. Liegt die Zahl zwischen 0 und 1, wird der Vektor kürzer, und wenn die Zahl 0 ist, erhält man den Nullvektor.

 

 

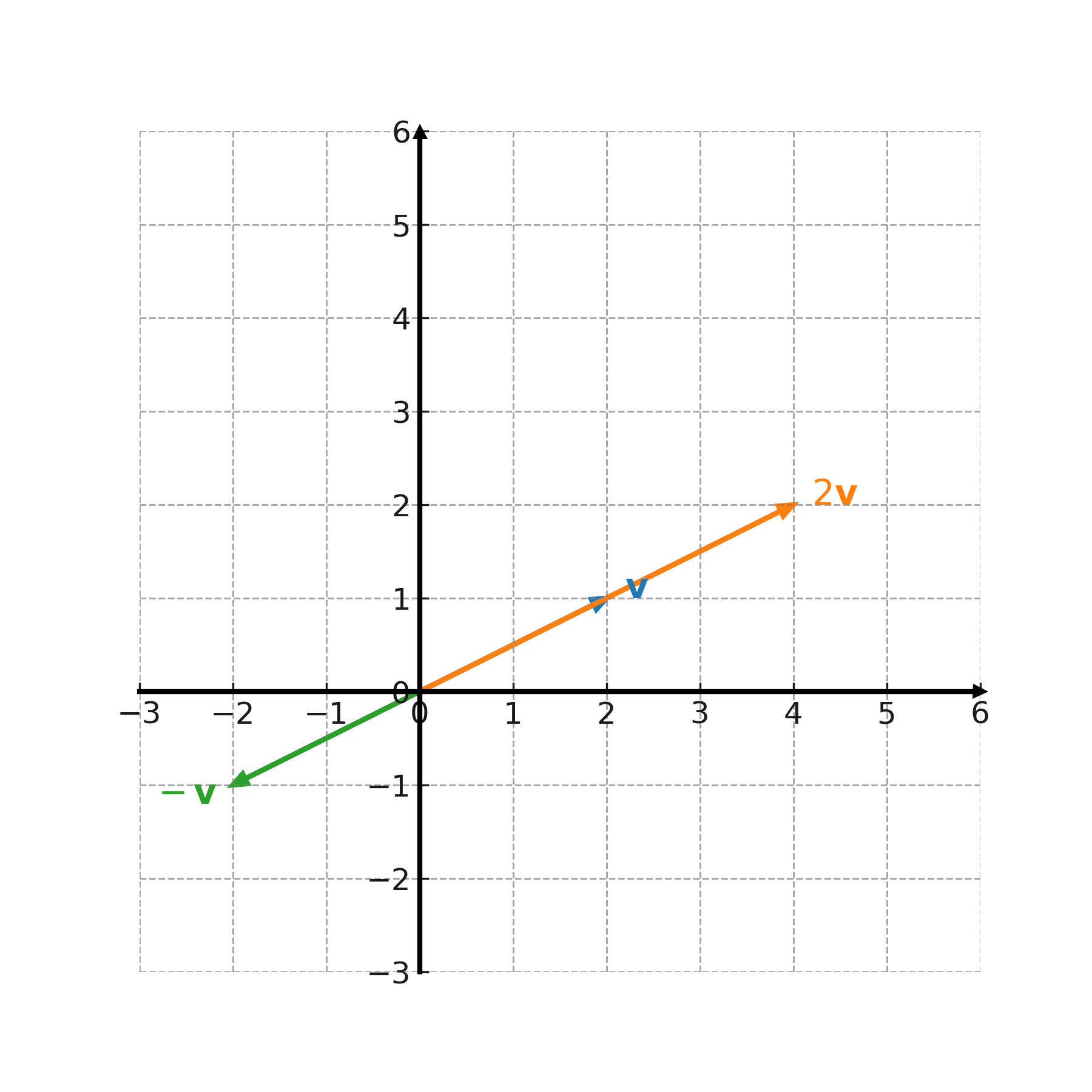
Anwendung

Die Multiplikation mit Zahlen wird verwendet, um die Größe einer Bewegung oder einer Kraft zu ändern. In der Physik entspricht dies einer Änderung der Stärke einer Kraft, ohne die Richtung zu ändern.

 

In der Mathematik wird die Multiplikation mit Parametern verwendet, um Geraden und Kurven zu beschreiben, zum Beispiel \( \large (x,y) = (x_0,y_0) + t \cdot \mathbf{r} \), wobei \( \large t \) eine Zahl ist und \( \large \mathbf{r} \) ein Richtungsvektor.