Länge und Einheitsvektoren

Die Länge eines Vektors beschreibt, wie groß der Vektor ist, während ein Einheitsvektor ein Vektor mit der Länge 1 in derselben Richtung wie der ursprüngliche ist.

 

Länge

Für einen Vektor \( \large \mathbf{v} = (x,y) \) berechnet sich die Länge durch:

 

$$ \large |\mathbf{v}| = \sqrt{x^2 + y^2} $$

 

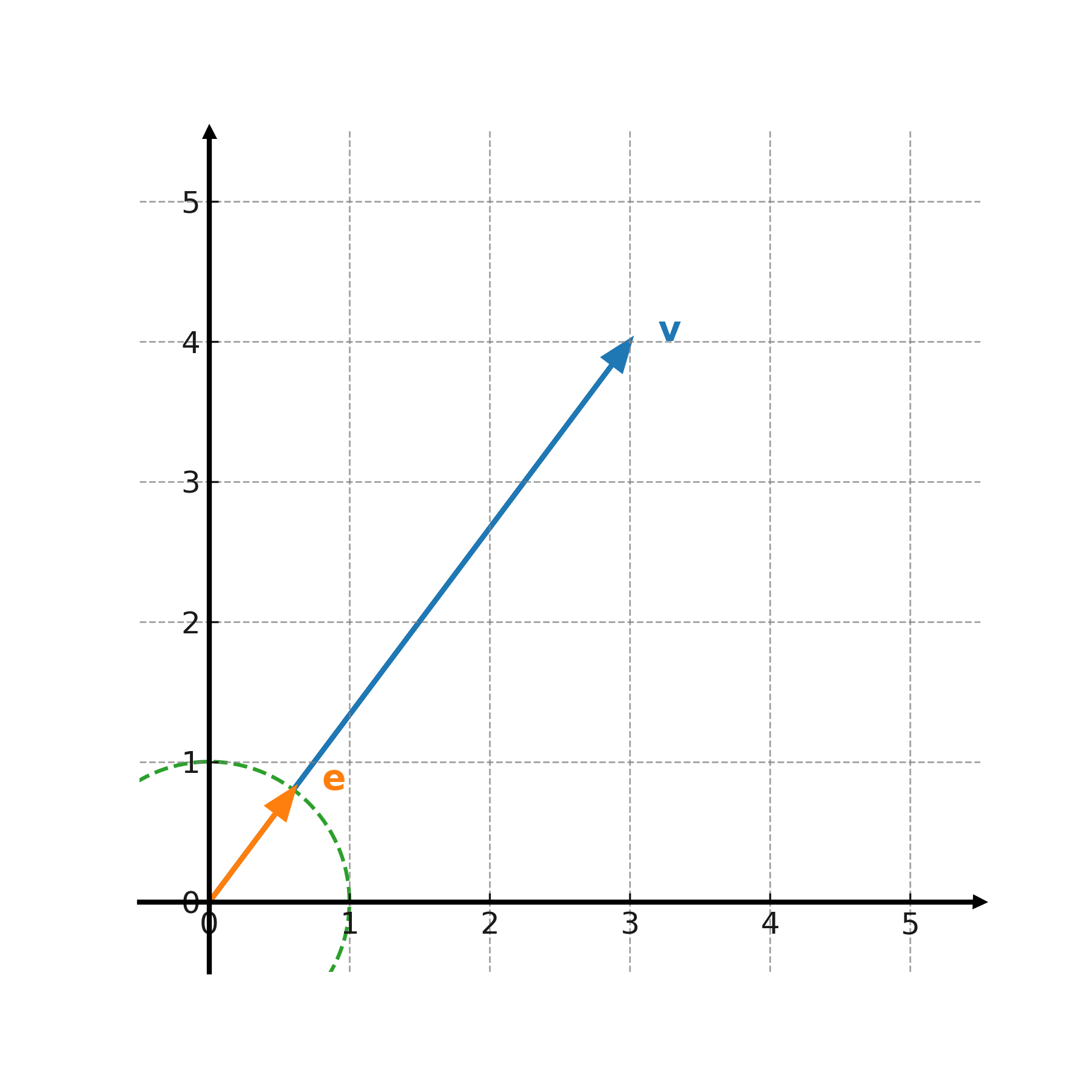
Beispiel: Der Vektor \( \large \mathbf{v} = (3,4) \) hat die Länge

 

$$ \large |\mathbf{v}| = \sqrt{3^2 + 4^2} = 5 $$

 

Einheitsvektor

Ein Einheitsvektor wird gefunden, indem man einen Vektor durch seine Länge teilt:

 

$$ \large \mathbf{e} = \frac{1}{|\mathbf{v}|} \cdot \mathbf{v} $$

 

Beispiel: Für \( \large \mathbf{v} = (3,4) \) erhält man

 

$$ \large \mathbf{e} = \frac{1}{5} \cdot (3,4) = \left(\frac{3}{5}, \frac{4}{5}\right) $$

 

Hinweis: Der Nullvektor \( \large (0,0) \) kann nicht zu einem Einheitsvektor gemacht werden, da seine Länge 0 ist und man nicht durch 0 teilen kann.

 

Die bekanntesten Einheitsvektoren sind die Standardeinheitsvektoren im Koordinatensystem:

 

$$ \large \mathbf{i} = (1,0), \quad \mathbf{j} = (0,1) $$

 

Geometrische Interpretation

Die Länge eines Vektors entspricht dem Abstand vom Ursprung zum Endpunkt des Vektors.

Ein Einheitsvektor ist ein Pfeil in derselben Richtung, aber immer mit der Länge 1.

 

 

Anwendung

Einheitsvektoren werden verwendet, um Richtungen zu beschreiben, ohne dass die Größe eine Rolle spielt. In der Physik werden sie zum Beispiel verwendet, um die Richtung einer Kraft unabhängig von ihrer Stärke anzugeben, und in der Mathematik werden sie zur Definition der Achsen von Koordinatensystemen genutzt.