Fläche mit Vektoren

Die Fläche einer Figur kann mit Hilfe von Vektoren berechnet werden. Besonders Parallelogramme und Dreiecke lassen sich durch eine einfache Formel ausdrücken, wenn sie durch zwei Vektoren beschrieben werden.

 

 

Fläche von Parallelogramm und Dreieck

Für zwei Vektoren \( \large \mathbf{u} \) und \( \large \mathbf{v} \) in der Ebene gilt, dass die Fläche des von ihnen aufgespannten Parallelogramms ist:

 

$$ \large A = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \sin(\theta) $$

 

wobei \( \large \theta \) der Winkel zwischen den Vektoren ist. Die Formel ergibt sich aus Grundlinie mal Höhe, wobei die Höhe als Projektion des einen Vektors auf eine Richtung senkrecht zum anderen bestimmt wird.

 

Eine andere Methode ist die Verwendung der Determinante:

 

$$ \large A = \left| \det \begin{pmatrix} x_1 & x_2 \\ y_1 & y_2 \end{pmatrix} \right| $$

 

wenn \( \large \mathbf{u} = (x_1,y_1) \) und \( \large \mathbf{v} = (x_2,y_2) \).

 

 

Beispiel

Wir nehmen \( \large \mathbf{u} = (3,2) \) und \( \large \mathbf{v} = (1,4) \).

 

$$ \large A = \left| \det \begin{pmatrix} 3 & 1 \\ 2 & 4 \end{pmatrix} \right| = |3 \cdot 4 - 2 \cdot 1| = |10| = 10 $$

 

Die Fläche des Parallelogramms beträgt 10. 

Die Fläche des von denselben beiden Vektoren aufgespannten Dreiecks ist die Hälfte, also \( \large 5 \).

 

 

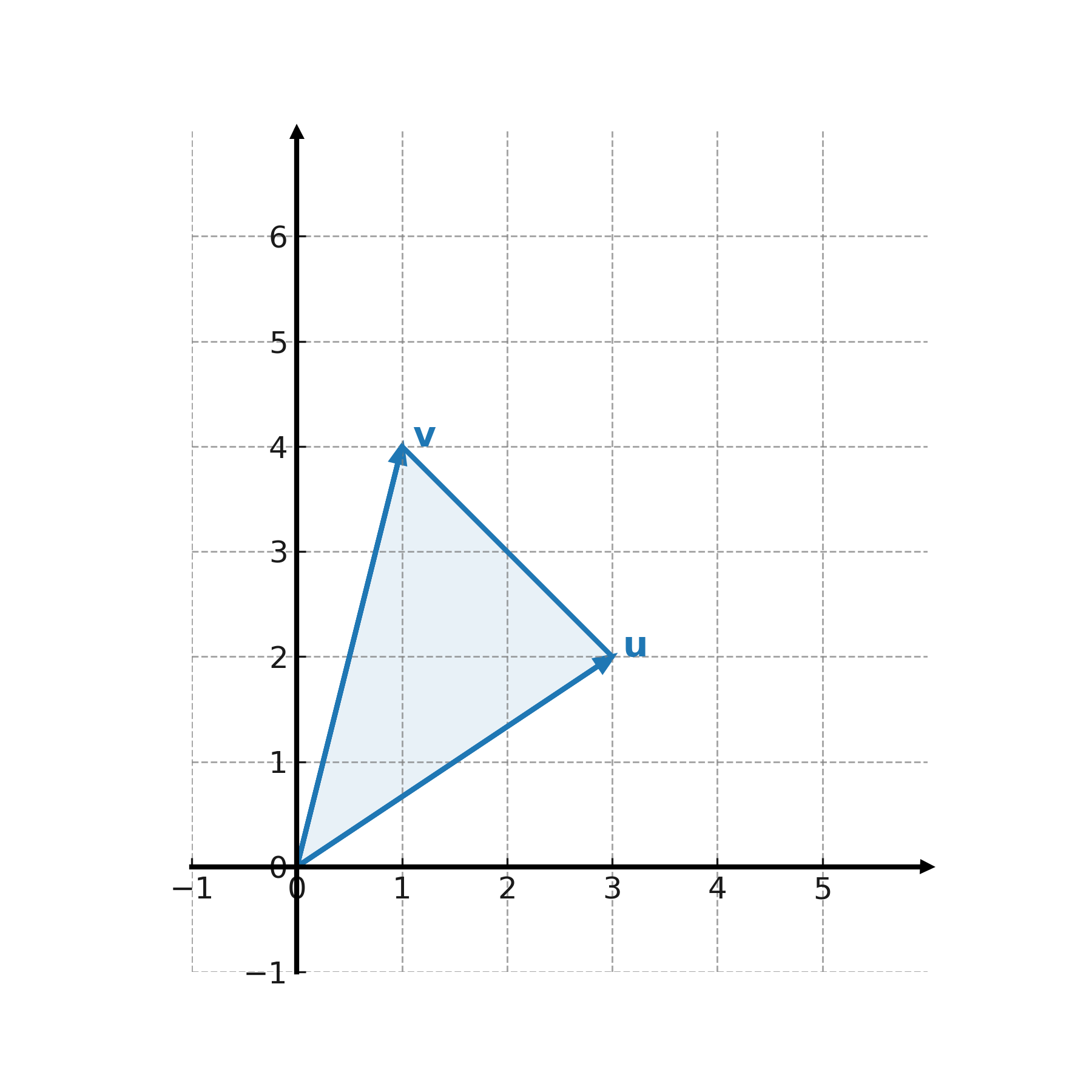
Geometrische Interpretation

Das Wichtigste ist, dass die Fläche als Grundlinie mal Höhe berechnet werden kann und dass die Höhe mit Hilfe der Projektion gefunden werden kann. Somit hängt der Begriff Projektion eng mit der Flächenberechnung zusammen.

 

 

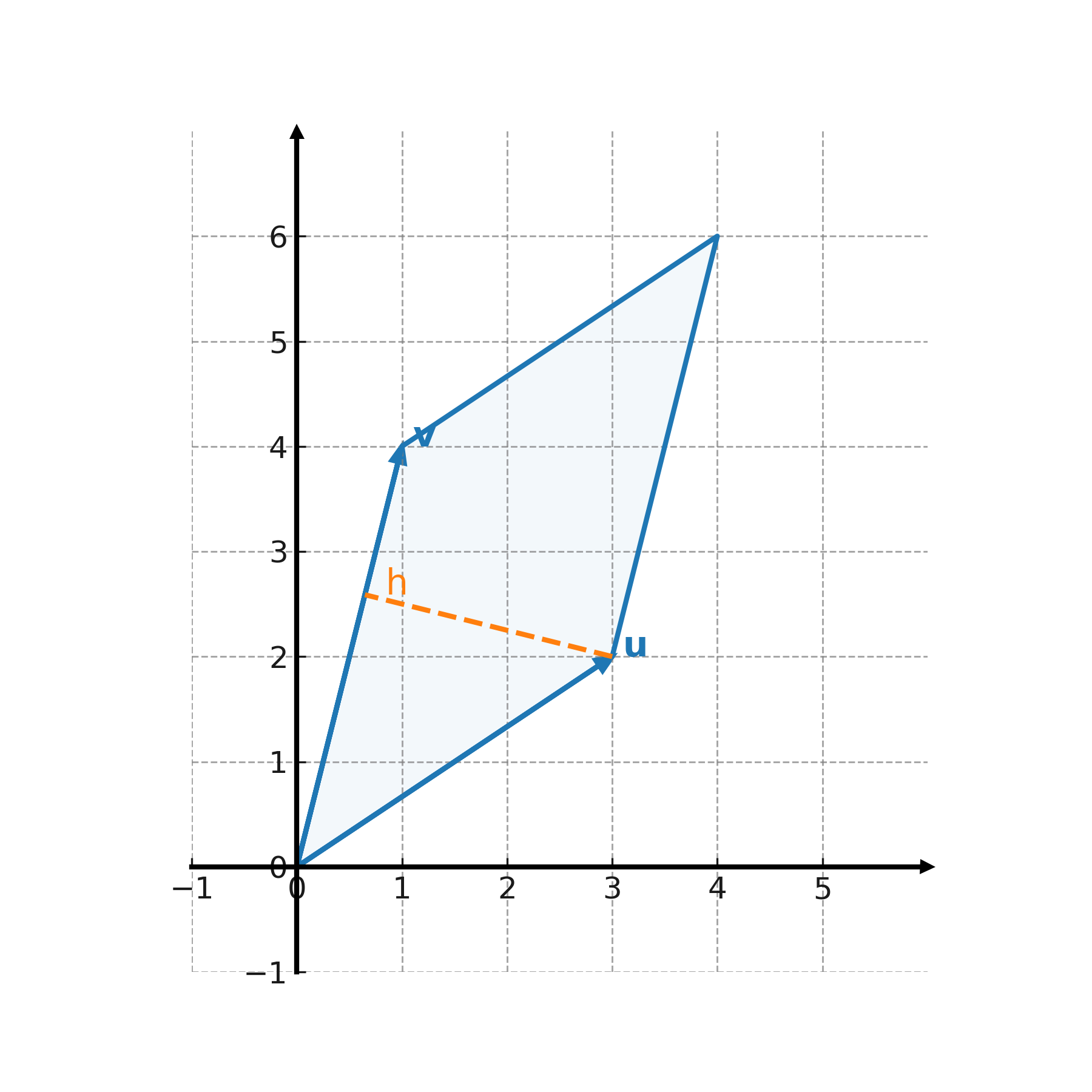
Anwendung

Vektorbasierte Formeln für Flächen werden sowohl in der Geometrie als auch in der linearen Algebra verwendet. Sie bieten eine einfache Methode zur Berechnung von Flächen in Koordinatensystemen und bilden die Grundlage für weitere Themen wie Determinanten und Volumen.