Sinussatz
Der Sinussatz kann in den Fällen verwendet werden, in denen man ein Winkel-Seiten-Paar kennt, also wenn eine der bekannten Seiten gegenüber dem bekannten Winkel liegt.
Das heißt, wenn du den Winkel \(A\) und die Seiten \(a\) und \(b\) kennst, solltest du den Sinussatz verwenden.
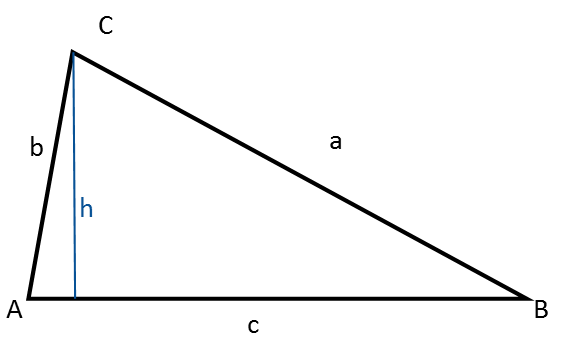
Ein beliebiges Dreieck ist weder rechtwinklig, gleichseitig noch gleichschenklig.
Der Sinussatz lautet wie folgt:
$$ {a \over \sin(A)} = {b \over \sin(B)} = {c \over \sin(C)} $$
Wenn du also den Winkel \(A\) und die Seiten \(a\) und \(b\) kennst und den Winkel \(B\) berechnen musst, verwendest du Folgendes und isolierst den Winkel \(B\):
$$ {a \over \sin(A)} = {b \over \sin(B)} \Leftrightarrow \\[16pt] \sin(B) = {b \cdot \sin(A) \over a} $$
Das Ergebnis wird eine Zahl zwischen 0 und 1 sein, zum Beispiel 0,866. Um den Winkel zu finden, musst du \( \sin^{-1} \) auf deinem Taschenrechner verwenden:
$$ \sin^{-1}(0,866) = 60^\circ $$
Der Winkel beträgt also 60 Grad.
Wenn du zwei Winkel und nur eine Seite kennst, kannst du den Sinussatz ebenfalls anwenden. Nehmen wir an, du kennst die Winkel \(A\) und \(B\) sowie die Seite \(a\):
$$ {a \over \sin(A)} = {b \over \sin(B)} \Leftrightarrow \\[16pt] b = {a \cdot \sin(B) \over \sin(A)} $$
Hinweis: Wenn die Berechnung \(\sin(v) > 1\) ergibt, gibt es keine Lösung. Das bedeutet, dass das angegebene Dreieck mit den vorhandenen Angaben nicht existieren kann.
Sinus und stumpfwinklige Dreiecke
Wenn du Winkel mit dem Sinus in einem Dreieck berechnest, das sich als stumpfwinklig herausstellt, musst du vorsichtig sein, da es zwei Ergebnisse geben kann, abhängig davon, wie viele Informationen du über das Dreieck hast.
Nehmen wir an, du hast die folgenden Angaben zu einem Dreieck:
- Winkel A = 25 Grad
- Seite a = 3
- Seite c = 5
Mit diesen Angaben können wir den Winkel \(C\) berechnen:
$$ \begin{align}{a \over \sin(A)} &= {c \over \sin(C)} \Leftrightarrow \\[10pt] \sin(C) &= {c \cdot \sin(A) \over a } \Leftrightarrow \\[10pt] \sin(C) &= {5 \cdot \sin(25^\circ) \over 3 } \Leftrightarrow \\[10pt] \sin(C) &= 0,704 \Leftrightarrow \\[10pt] \sin^{-1}(0,704) &= 44,78^\circ \end{align} $$
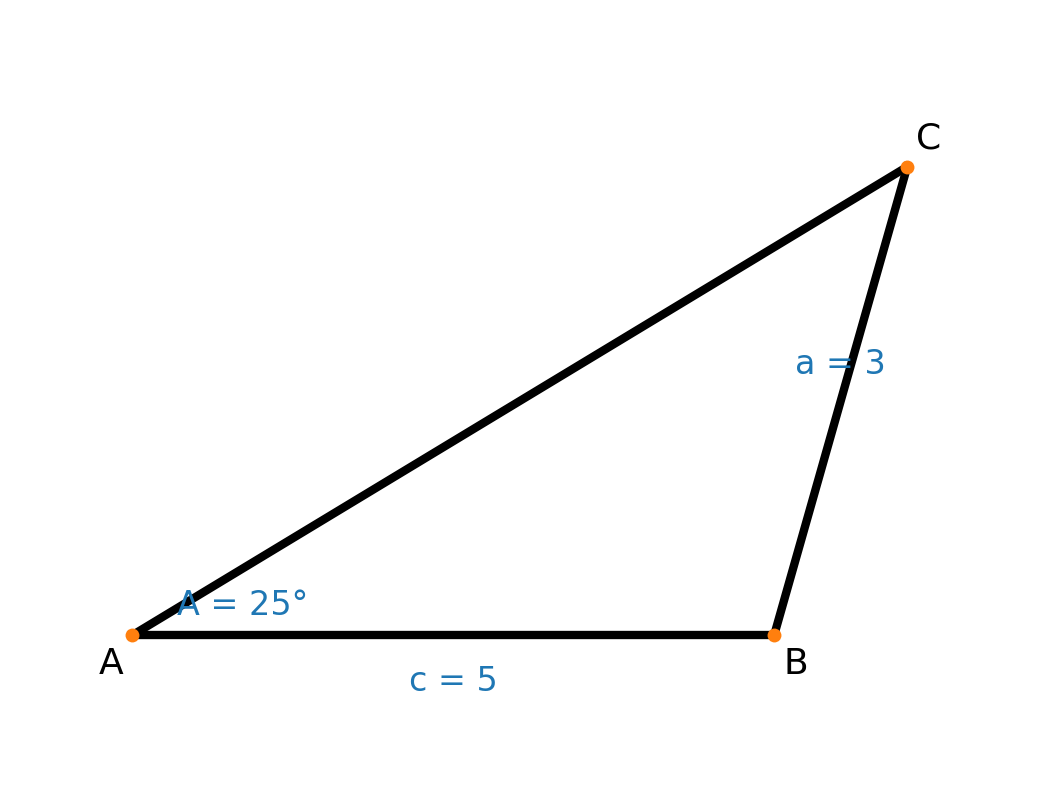
Das Ergebnis ist also ein Dreieck, wie oben dargestellt, mit:
- Winkel A = 25°
- Winkel B = 110,22°
- Winkel C = 44,78°
Berechnung des stumpfen Winkels
Wenn du dir die Abbildung unten ansiehst, kannst du erkennen, dass es möglich ist, ein weiteres Dreieck mit denselben Angaben zu zeichnen.
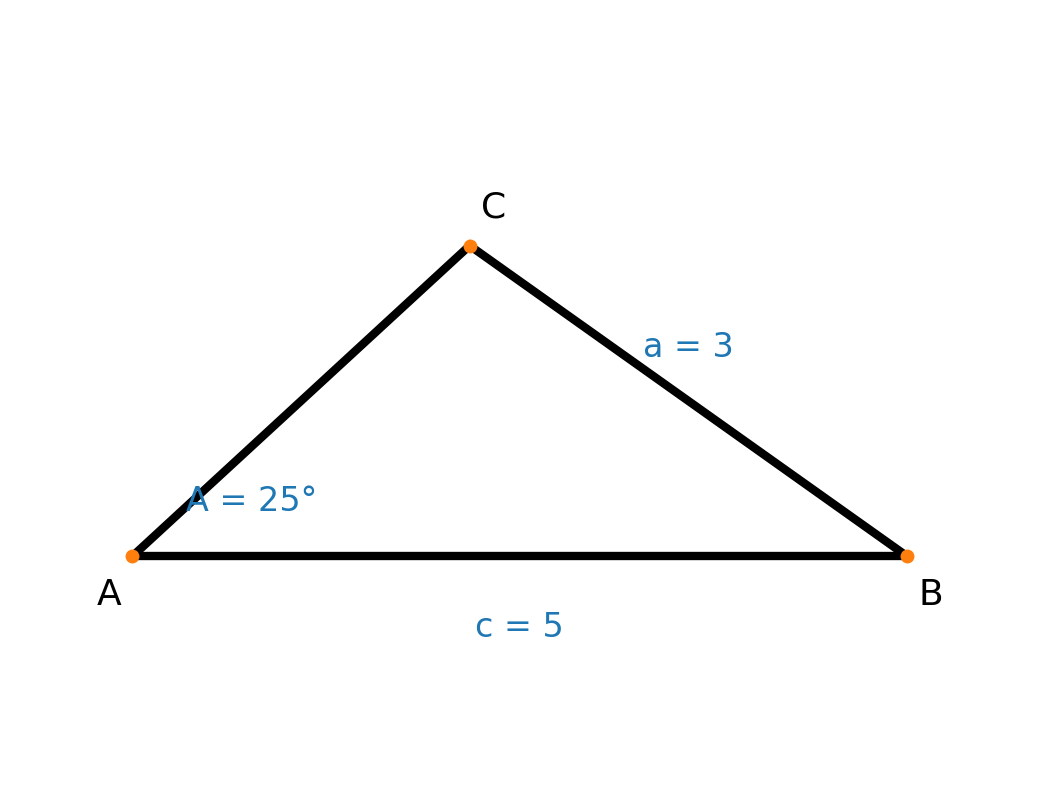
Der Sinussatz liefert immer die spitze Lösung (zwischen 0° und 90°). Die mögliche stumpfe Lösung erhält man, indem man den gefundenen spitzen Winkel von 180° abzieht.
Wir nehmen an, dass der spitze Winkel 44,78° beträgt, wie zuvor berechnet, und nennen ihn \(C_1\). Den stumpfen Winkel nennen wir \(C_2\):
$$ C_2 = 180 - C_1 \Leftrightarrow \\[12pt] C_2 = 135,22^\circ $$
Nun kennst du den Winkel \(C\) für beide Dreiecke und kannst den Rest für beide berechnen. Das bedeutet, dass die Seite \(b\) ebenfalls zwei verschiedene Längen hat (gleiches gilt für Umfang, Höhe und Fläche).
Daher solltest du beim Anwenden des Sinussatzes immer überprüfen, ob die gefundene Lösung einen stumpfen Winkel haben kann.
Die Regel, wann es zwei Lösungen gibt, lautet: Wenn der Winkel, den du mit dem Sinussatz berechnest, kleiner als 90 Grad ist, wird es zwei Ergebnisse geben.