Trigonometrie
Die Trigonometrie ist die Lehre von den Zusammenhängen zwischen den Seiten und Winkeln eines Dreiecks und von der Berechnung der unbekannten Größen aus denen, die man kennt.
Die ebene Trigonometrie befasst sich mit den Beziehungen in einem ebenen Dreieck.
Ausgehend vom Einheitskreis und dem Wissen über trigonometrische Funktionen und Relationen ist es möglich, nahezu alle geometrischen Figuren zu berechnen, auch räumliche.

Wenn man sich den Einheitskreis in einem Koordinatensystem vorstellt, liegt das Zentrum des Kreises bei (0,0), und er hat einen Radius von 1.
Aus dem Einheitskreis lassen sich drei Funktionen definieren, Kosinus, Sinus und Tangens, die zur Berechnung der Winkel und Seiten von Dreiecken verwendet werden.
Der Umfang des Einheitskreises beträgt \( \large 2 \cdot \pi \).
Die Fläche des Einheitskreises beträgt \( \large \pi \).
Funktionen und Relationen
Es gibt insgesamt sechs trigonometrische Funktionen. In einem rechtwinkligen Dreieck werden sie wie folgt definiert:
| Funktion | Definition |
|---|---|
| Sinus (sin) | \( \Large \sin(v) = \tfrac{\text{Gegenkathete}}{\text{Hypotenuse}} \) |
| Kosinus (cos) | \( \Large \cos(v) = \tfrac{\text{Ankathete}}{\text{Hypotenuse}} \) |
| Tangens (tan) | \( \Large \tan(v) = \tfrac{\text{Gegenkathete}}{\text{Ankathete}} \) |
| Kotangens (cot) | \( \Large \cot(v) = \tfrac{\text{Ankathete}}{\text{Gegenkathete}} \) |
| Sekans (sec) | \( \Large \sec(v) = \tfrac{\text{Hypotenuse}}{\text{Ankathete}} \) |
| Kosekans (csc) | \( \Large \csc(v) = \tfrac{\text{Hypotenuse}}{\text{Gegenkathete}} \) |
Für die gewöhnliche Geometrie sind die ersten drei die wichtigsten. Es ist auch wichtig, die Sinus- und Kosinusrelationen anwenden zu können.
Referenzlinie, -punkt und -winkel
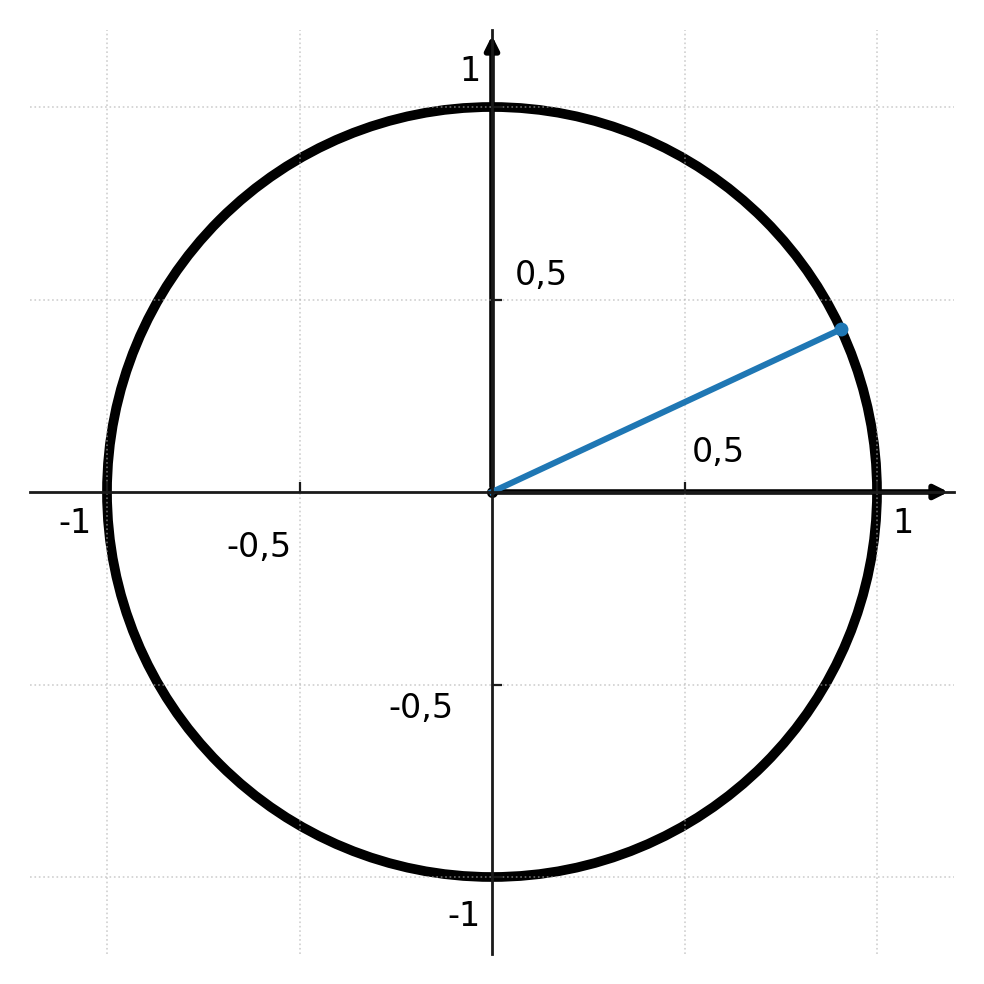
Wenn man eine Linie vom Zentrum (0,0) zu einem beliebigen Punkt auf dem Kreisbogen zieht, bildet die Linie einen Winkel mit der x-Achse des Koordinatensystems.
Der Punkt, den man auf dem Kreisbogen gewählt hat, wird Referenzpunkt genannt. Die gezogene Linie heißt Referenzlinie, und der mit der x-Achse gebildete Winkel heißt Referenzwinkel.
Wenn man den Winkel in einem Dreieck kennt, kann man ihn in den Kreis einzeichnen, und der Referenzpunkt ist die Grundlage für die Berechnung des Dreiecks.
Sphärische Trigonometrie
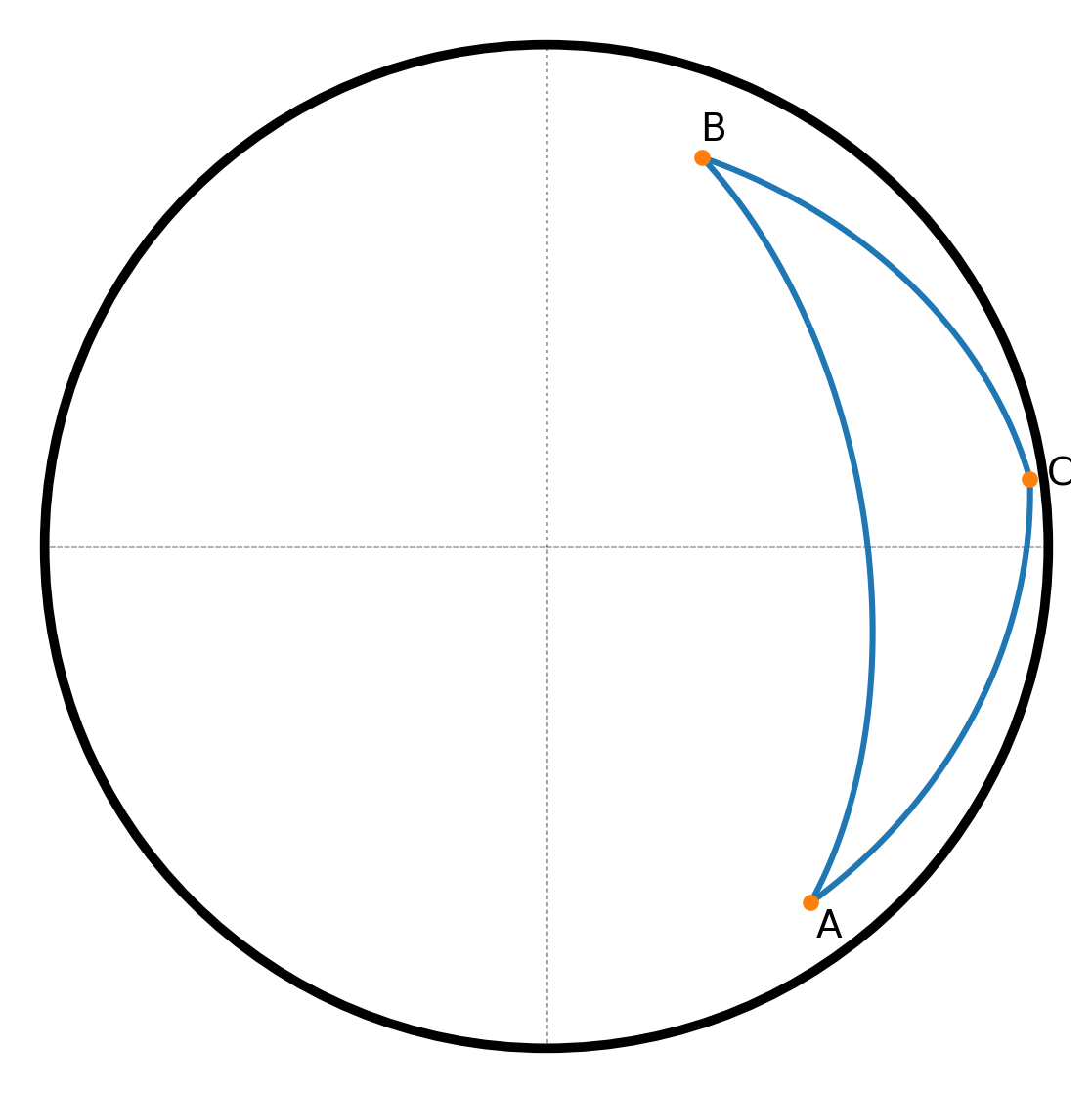
Die sphärische Trigonometrie befasst sich mit Dreiecken und anderen geometrischen Figuren auf der Oberfläche einer Kugel.
So wie es in der ebenen Trigonometrie den Einheitskreis mit Radius 1 gibt, kann man sich eine Einheitskugel mit Radius 1 vorstellen.
Ein sphärisches Dreieck wird durch drei Bögen von Großkreisen auf der Oberfläche der Kugel gebildet. Mithilfe trigonometrischer Funktionen lassen sich die gegenseitigen Abhängigkeiten zwischen Seiten und Winkeln solcher Dreiecke berechnen.
Die sphärische Trigonometrie wurde insbesondere für die Navigation und die Astronomie entwickelt.