Tangens und Kotangens
Die Tangensfunktion ist ebenfalls eine trigonometrische Funktion, die etwas über den Winkel im Einheitskreis aussagt. Im Gegensatz zu Kosinus und Sinus kann das Ergebnis größer als 1 sein.
Die Definition des Tangens lautet:
$$ tan(v) = \frac{sin(v)}{cos(v)} $$
Das bedeutet, dass ein Winkel (A) von 25 Grad so berechnet wird:
$$ tan(v) = \frac{sin(v)}{cos(v)} \qquad \Leftrightarrow $$
$$ tan(v) = \frac{sin(25^\circ)}{cos(25^\circ)} \qquad \Leftrightarrow $$
$$ tan(v) = \frac{0.423}{0.906} \qquad \Leftrightarrow $$
$$ tan(v) \approx 0.467 $$
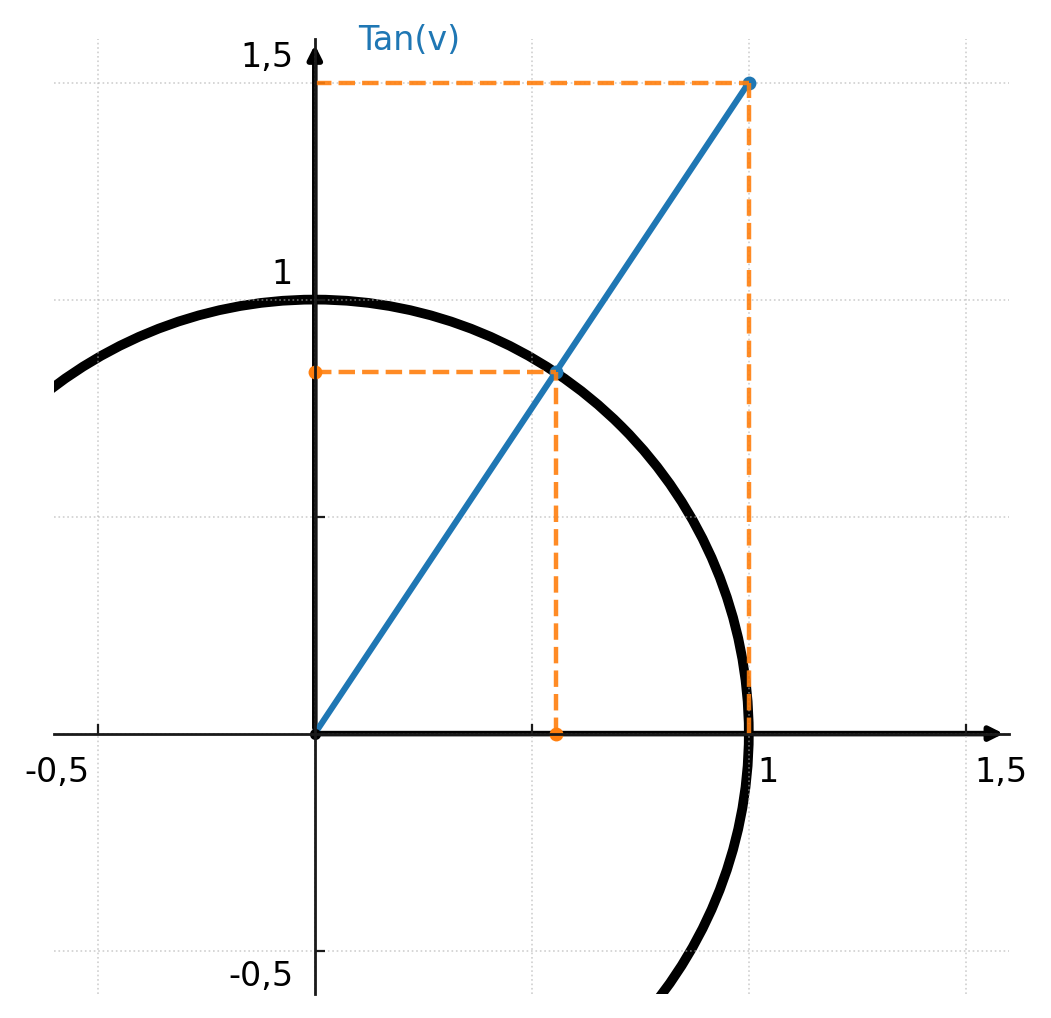
Der Tangens kann auch im Einheitskreis abgelesen werden. Man beginnt damit, eine vertikale Linie zu zeichnen, die den Einheitskreis im Punkt \((1, 0)\) tangiert.
Dann kann man sehen, wo der Winkel die Linie schneidet. Die y-Koordinate des Schnittpunkts ist der Tangens des Winkels.
Kotangens
Der Kotangens ist das Gegenstück zum Tangens:
$$ cot(v) = \frac{cos(v)}{sin(v)} $$
Der Kotangens wird nicht so häufig verwendet, da Sinus, Kosinus und Tangens die gängigsten geometrischen Berechnungen ermöglichen.
Auf gewöhnlichen Taschenrechnern findet man in der Regel auch keine cot-Taste.
Im Einheitskreis verläuft der Kotangens horizontal vom Punkt \((0,1)\) aus und wird auf der x-Achse abgelesen, wo er den Winkel schneidet:
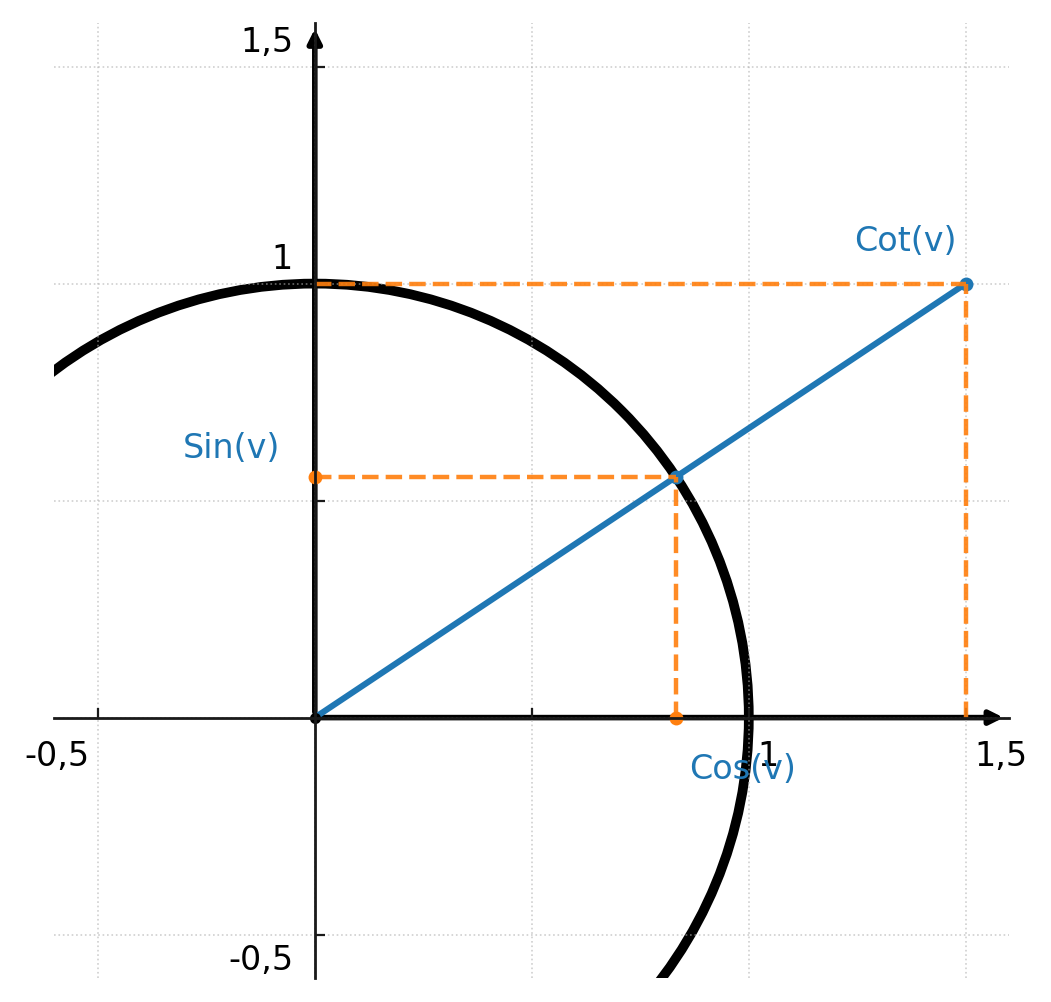
Der Winkel von 25 Grad wird so berechnet:
$$ cot(v) = \frac{cos(v)}{sin(v)} \qquad \Leftrightarrow $$
$$ cot(v) = \frac{cos(25^\circ)}{sin(25^\circ)} \qquad \Leftrightarrow $$
$$ cot(v) = \frac{0.906}{0.423} \qquad \Leftrightarrow $$
$$ cot(v) \approx 2.14 $$
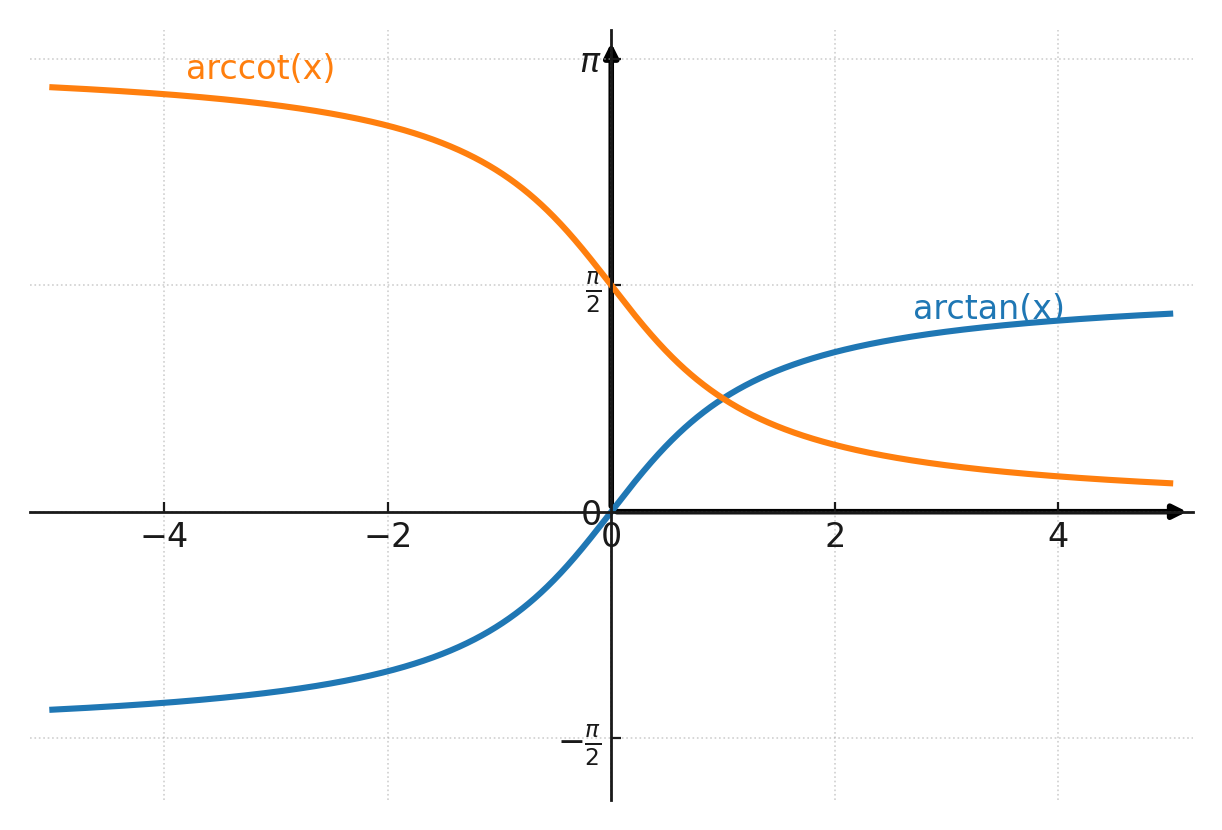
Inverse Funktionen
Wie bei Arcsin und Arccos gibt es auch inverse Funktionen für Tangens und Kotangens. Diese heißen Arctan und Arccot (oder werden als tan-1 und cot-1 geschrieben).
Wenn man den Tangens eines Winkels kennt, aber nicht den Winkel selbst, kann man ihn mit Arctan berechnen. Zum Beispiel wissen wir:
$$ tan(45^\circ) = 1 $$
Daraus folgt auch:
$$ tan^{-1}(1) = 45^\circ $$
Arctan kann verwendet werden, um einen Winkel aus dem Verhältnis zweier Seiten in einem rechtwinkligen Dreieck zu berechnen.
Arccot funktioniert auf die gleiche Weise für den Kotangens. Wenn man den Kotangens eines Winkels kennt, kann man den Winkel mit Arccot berechnen. Zum Beispiel:
$$ cot(45^\circ) = 1 \qquad \Leftrightarrow \qquad cot^{-1}(1) = 45^\circ $$
Beide Funktionen liefern zwei Lösungen, wenn sie nicht eingeschränkt werden. Hier sieht man die zwei Lösungen der Arctan-Funktion im ersten und dritten Quadranten:
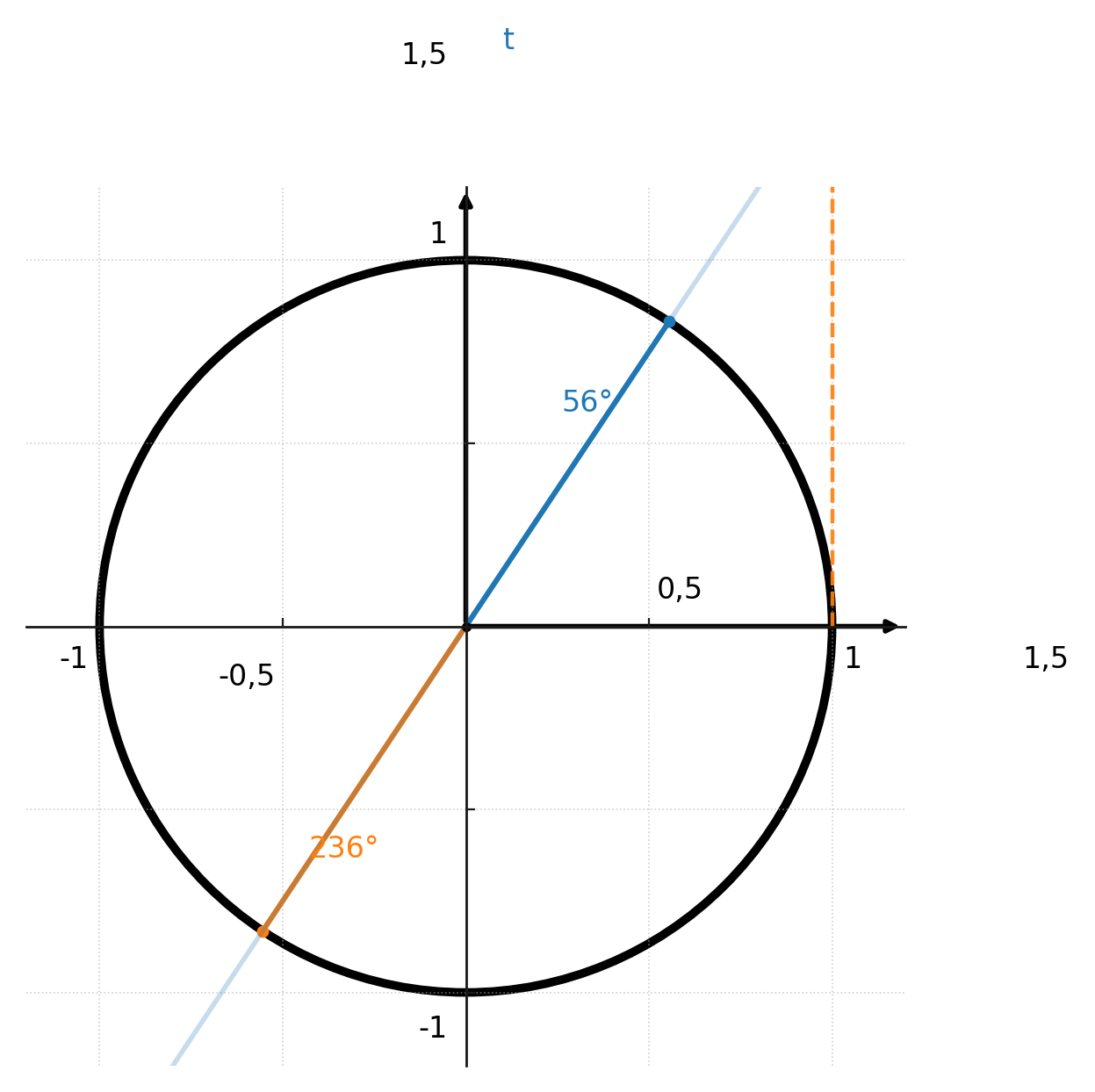
Die Funktionen werden wie folgt eingeschränkt:
- Für Arctan wird der Winkel auf das Intervall \(-90^\circ \leq v \leq 90^\circ\) beschränkt
- Für Arccot wird der Winkel auf das Intervall \(0^\circ \leq v \leq 180^\circ\) beschränkt
Dadurch werden die Funktionen eindeutig!
Die beiden inversen Funktionen sind im Koordinatensystem dargestellt. Beachten Sie, dass die y-Achse in Radiant und nicht in Grad angegeben ist.