Relationen

In der Trigonometrie sind Relationen die Formeln und Zusammenhänge, die die trigonometrischen Funktionen miteinander verbinden. Während die Funktionen (Sinus, Kosinus, Tangens usw.) jeweils ein bestimmtes Verhältnis beschreiben, zeigen die Relationen, wie die Funktionen zusammenhängen und zur Berechnung von Seiten und Winkeln in Dreiecken verwendet werden können.

 

Pythagoreische Identität

Eine der grundlegendsten Relationen ist die pythagoreische Identität, die den Zusammenhang zwischen Sinus und Kosinus für jeden Winkel zeigt:

 

$$ \sin^2(v) + \cos^2(v) = 1 $$

 

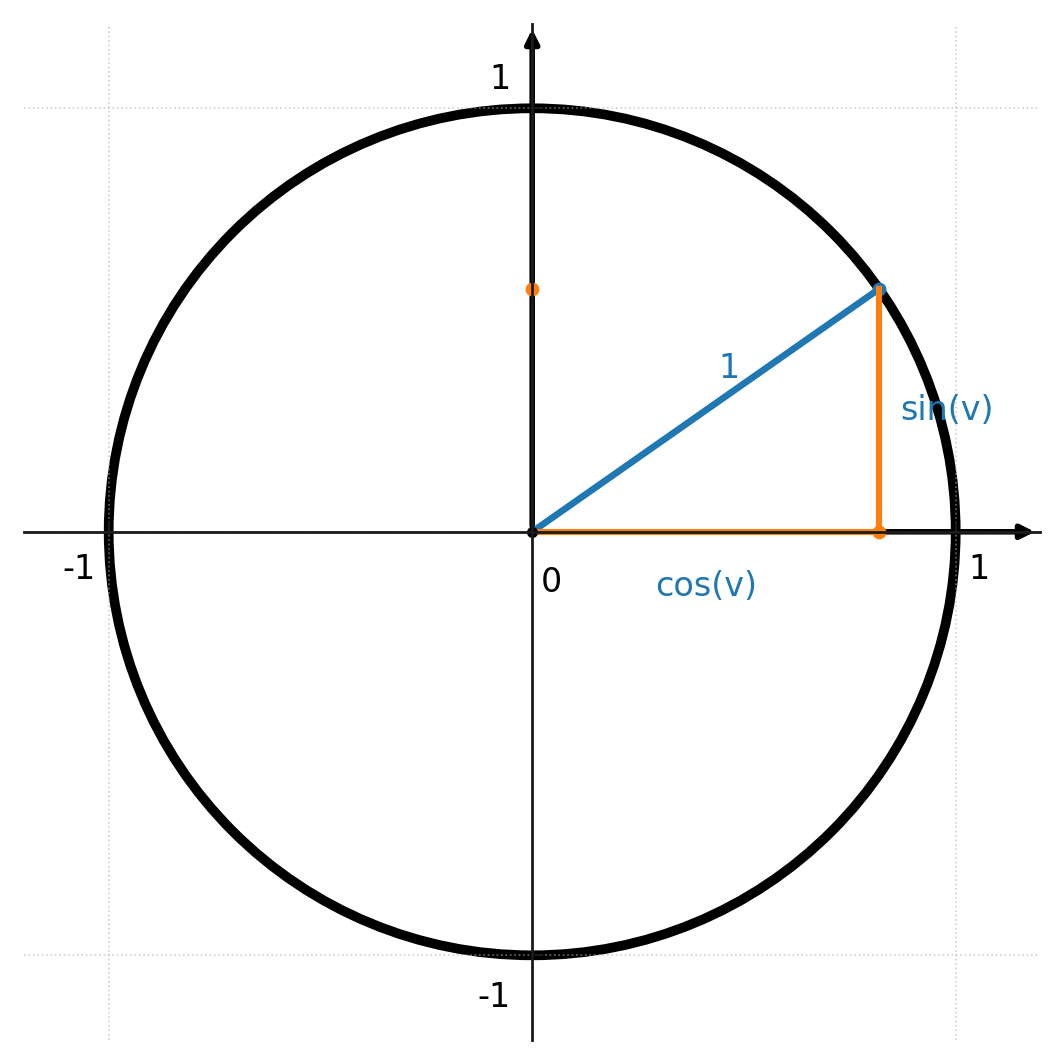
Die Identität folgt direkt aus dem Einheitskreis.

Wenn ein Punkt auf dem Kreis die Koordinaten \( (\cos v, \sin v) \) hat, gilt der Satz des Pythagoras, da der Radius immer 1 ist:

 

$$ (\cos v)^2 + (\sin v)^2 = 1^2 = 1 $$

 

 

Anwendung

Die pythagoreische Identität ermöglicht es, den Sinus zu berechnen, wenn der Kosinus bekannt ist, oder den Kosinus, wenn der Sinus bekannt ist.

Sie bildet auch die Grundlage für viele andere trigonometrische Identitäten.

 

Beispiel: Wenn \( \cos v = 0.6 \), kann man den Sinus wie folgt berechnen:

 

$$ \sin^2(v) = 1 - \cos^2(v) = 1 - 0.6^2 = 0.64 $$

$$ \sin(v) = \pm \sqrt{0.64} = \pm 0.8 $$

 

Beachte, dass es zwei Lösungen gibt, da der Winkel sowohl im ersten als auch im zweiten Quadranten liegen kann.

 

Die pythagoreische Identität ist die grundlegendste trigonometrische Relation und bildet die Grundlage für viele andere Formeln und Berechnungen in der Trigonometrie.