Kosinussatz

Der Kosinussatz kann in beliebigen Dreiecken verwendet werden – also in Dreiecken, die weder rechtwinklig, gleichschenklig noch gleichseitig sind. Er funktioniert sowohl dann, wenn man zwei Seiten und den eingeschlossenen Winkel kennt, als auch wenn man alle drei Seiten kennt.

 

Formeln des Kosinussatzes

Wenn man einen Winkel und die beiden Seiten kennt, die diesen Winkel bilden, kann man die dritte Seite mithilfe des Kosinussatzes berechnen:

 

$$ a^2 = b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos(A) $$

$$ b^2 = a^2 + c^2 - 2 \cdot a \cdot c \cdot \cos(B) $$

$$ c^2 = a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos(C) $$

 

Hinweis: Wenn das Dreieck rechtwinklig ist, genügt der Satz des Pythagoras. Der Kosinussatz ist besonders nützlich für beliebige Dreiecke.

 

Berechnung der Winkel

Wenn man alle drei Seiten eines Dreiecks kennt, kann man die Winkel berechnen, indem man den Kosinus in der Formel isoliert:

 

$$ \cos(A) = \frac{b^2 + c^2 - a^2}{2 \cdot b \cdot c} $$

$$ \cos(B) = \frac{a^2 + c^2 - b^2}{2 \cdot a \cdot c} $$

$$ \cos(C) = \frac{a^2 + b^2 - c^2}{2 \cdot a \cdot b} $$

 

Das Ergebnis wird eine Zahl zwischen -1 und 1 sein. Um den Winkel zu finden, verwendet man \( \cos^{-1} \) auf dem Taschenrechner:

 

$$ \cos^{-1}(0,866) = 30^\circ $$

 

Der Winkel beträgt also 30 Grad.

 

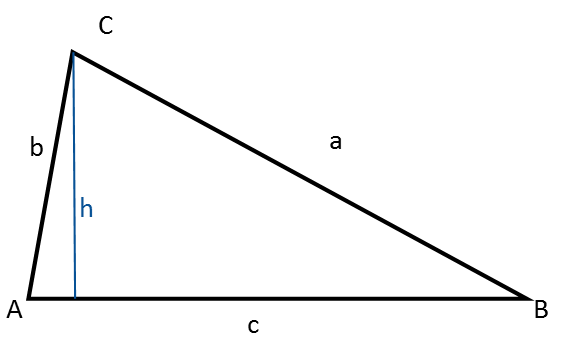
Ein beliebiges Dreieck ist weder rechtwinklig, noch gleichseitig, noch gleichschenklig.

Beachten Sie, dass die Höhe es in zwei rechtwinklige Dreiecke teilt.