Addition und Subtraktion von Winkeln
In der Trigonometrie beschreibt Addition und Subtraktion von Winkeln die Formeln, die zeigen, wie sich Sinus, Kosinus und Tangens ändern, wenn man zwei Winkel addiert oder subtrahiert.
Die Formeln ermöglichen es, Werte für neue Winkel aus bekannten zu berechnen.
Zum Beispiel kann man cos(75°) berechnen, auch wenn er nicht in den Tabellen steht, indem man cos(45° + 30°) verwendet.
Formeln für Addition und Subtraktion
Kosinus:
$$ \large \cos(\alpha + \beta) = \cos(\alpha) \cdot \cos(\beta) - \sin(\alpha) \cdot \sin(\beta) $$
$$ \large \cos(\alpha - \beta) = \cos(\alpha) \cdot \cos(\beta) + \sin(\alpha) \cdot \sin(\beta) $$
Sinus:
$$ \large \sin(\alpha + \beta) = \sin(\alpha) \cdot \cos(\beta) + \cos(\alpha) \cdot \sin(\beta) $$
$$ \large \sin(\alpha - \beta) = \sin(\alpha) \cdot \cos(\beta) - \cos(\alpha) \cdot \sin(\beta) $$
Tangens:
$$ \large \tan(\alpha + \beta) = \frac{\tan(\alpha) + \tan(\beta)}{1 - \tan(\alpha) \cdot \tan(\beta)} $$
$$ \large \tan(\alpha - \beta) = \frac{\tan(\alpha) - \tan(\beta)}{1 + \tan(\alpha) \cdot \tan(\beta)} $$
Beispiel
Wir möchten \( \cos(75^\circ) \) berechnen. Das kann man als \( \cos(45^\circ + 30^\circ) \) schreiben:
$$ \large \cos(75^\circ) = \cos(45^\circ + 30^\circ) $$
$$ \large = \cos(45^\circ) \cdot \cos(30^\circ) - \sin(45^\circ) \cdot \sin(30^\circ) $$
$$ \large = \tfrac{\sqrt{2}}{2} \cdot \tfrac{\sqrt{3}}{2} - \tfrac{\sqrt{2}}{2} \cdot \tfrac{1}{2} $$
$$ \large = \tfrac{\sqrt{6}}{4} - \tfrac{\sqrt{2}}{4} = \tfrac{\sqrt{6} - \sqrt{2}}{4} $$
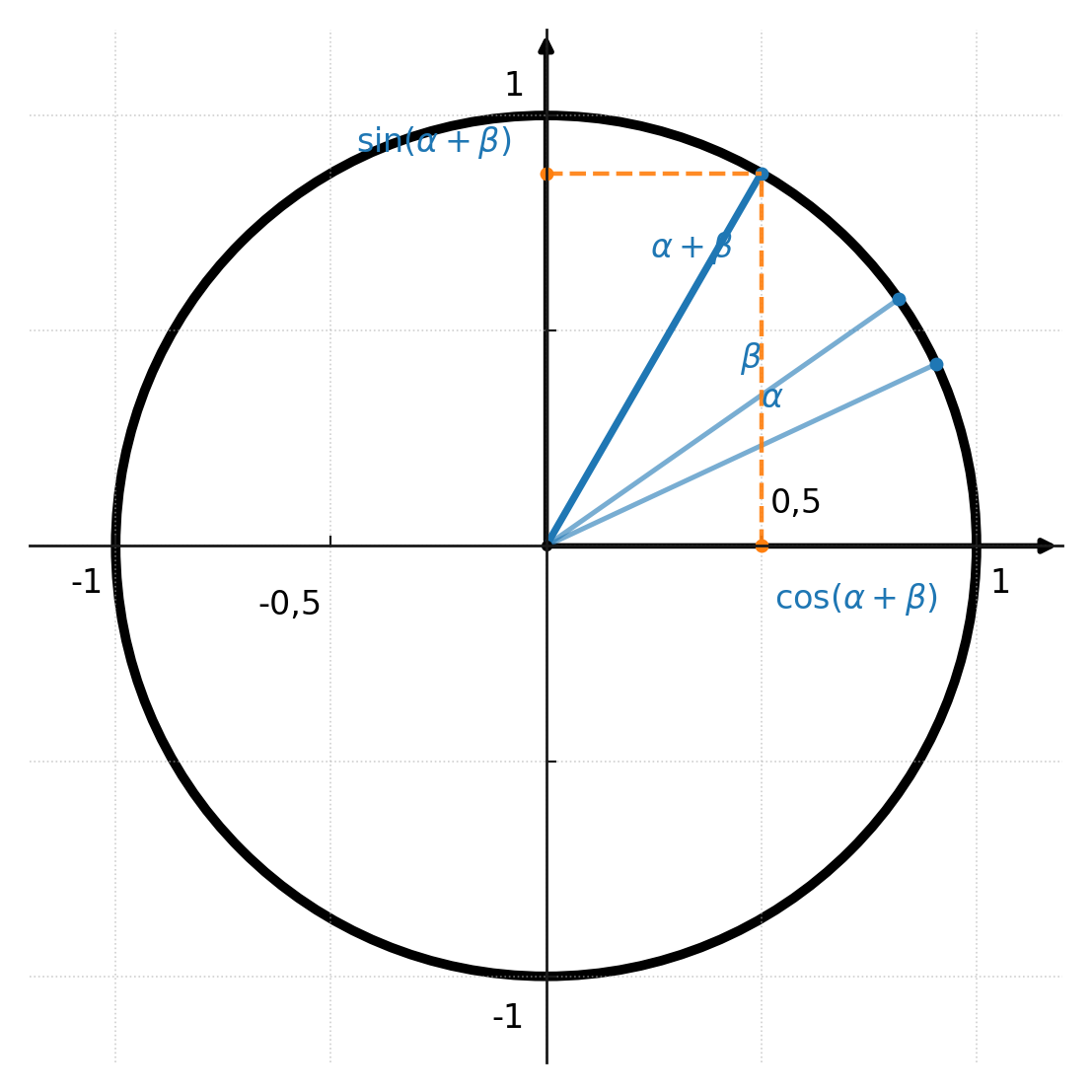
Die Formeln können auch geometrisch aus dem Einheitskreis verstanden werden.
Anwendungen
- Man kann exakte Werte für Winkel wie 15°, 75° und 105° berechnen.
- Die Formeln sind die Grundlage für Doppelwinkel- und Halbwinkel-Formeln (mit \( \alpha = \beta \)).
- Sie werden in Beweisen und Identitäten in der höheren Trigonometrie und Analysis verwendet.