Doppel- und Halbwinkel-Formeln

In der Trigonometrie beschreiben die Doppel und Halbwinkel Formeln, wie Sinus, Cosinus und Tangens ausgedrückt werden können, wenn der Winkel verdoppelt oder halbiert wird.

Die Formeln basieren direkt auf den Additions und Subtraktionsformeln und ermöglichen es, neue Zusammenhänge zwischen den trigonometrischen Funktionen zu finden.

 

Doppelwinkel Formeln

Wenn man \( \alpha = \beta \) in den Additionsformeln setzt, erhält man:

 

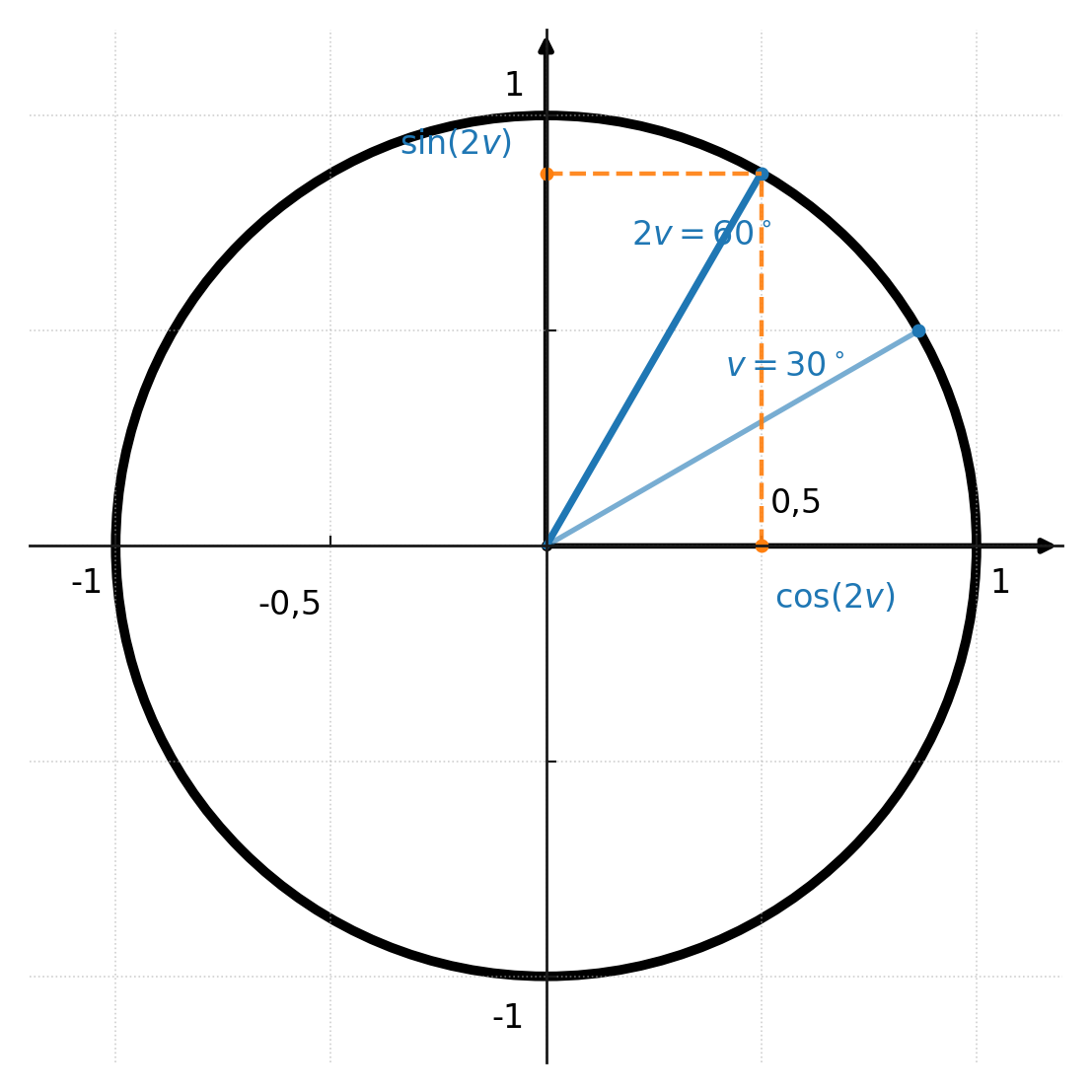
$$ \large \sin(2v) = 2 \sin(v) \cdot \cos(v) $$

$$ \large \cos(2v) = \cos^2(v) - \sin^2(v) $$

$$ \large \tan(2v) = \frac{2 \tan(v)}{1 - \tan^2(v)} $$

 

 

 

Die Cosinusformel kann mit Hilfe der Pythagoras Identität auch in andere nützliche Formen umgeschrieben werden:

 

$$ \large \cos(2v) = 2\cos^2(v) - 1 = 1 - 2\sin^2(v) $$

 

Halbwinkel Formeln

Die Halbwinkel Formeln erhält man, indem man \(\sin v\) und \(\cos v\) in den Doppelwinkel Formeln isoliert. Das Ergebnis lautet:

 

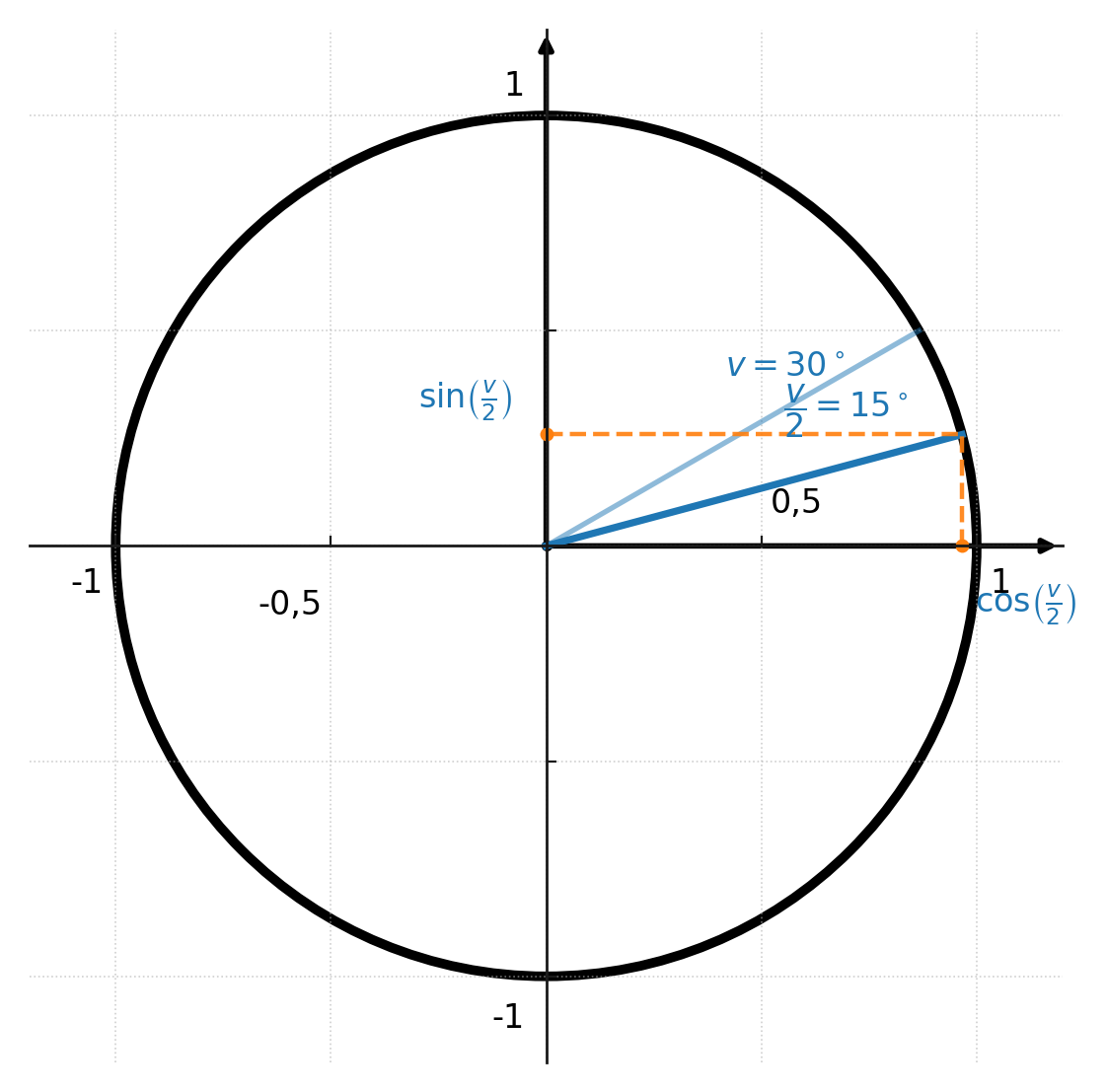
$$ \large \sin\!\left(\tfrac{v}{2}\right) = \pm \sqrt{\tfrac{1 - \cos(v)}{2}} $$

$$ \large \cos\!\left(\tfrac{v}{2}\right) = \pm \sqrt{\tfrac{1 + \cos(v)}{2}} $$

$$ \large \tan\!\left(\tfrac{v}{2}\right) = \tfrac{\sin(v)}{1 + \cos(v)} = \tfrac{1 - \cos(v)}{\sin(v)} $$

 

Die Vorzeichen \(+\) oder \(-\) hängen davon ab, in welchem Quadranten sich der Winkel befindet.

 

 

Beispiel

Wir wollen \( \sin(2 \cdot 30^\circ) \) berechnen:

 

$$ \large \sin(60^\circ) = 2 \cdot \sin(30^\circ) \cdot \cos(30^\circ) $$

$$ \large = 2 \cdot \tfrac{1}{2} \cdot \tfrac{\sqrt{3}}{2} = \tfrac{\sqrt{3}}{2} $$

 

Anwendung

• Die Formeln werden verwendet, um exakte Werte für Winkel wie 15°, 22,5° und 75° zu berechnen.
• Sie sind nützlich in Beweisen und trigonometrischen Umformungen.
• Die Halbwinkel Formeln werden oft zum Lösen trigonometrischer Gleichungen eingesetzt.