Sinus und Kosinus

Wenn man einen Winkel in den Einheitskreis einzeichnet, kann man Kosinus und Sinus auf dem Umfang des Einheitskreises als einen Punkt im Koordinatensystem ablesen.

Das Ergebnis wird immer zwischen -1 und 1 liegen, da der Punkt immer auf dem Kreis mit Radius 1 liegt.

In der Abbildung ist ein Winkel von 25 Grad in den Einheitskreis eingezeichnet, und wir können den Schnittpunkt auf der x- und y-Achse ablesen.

 

 

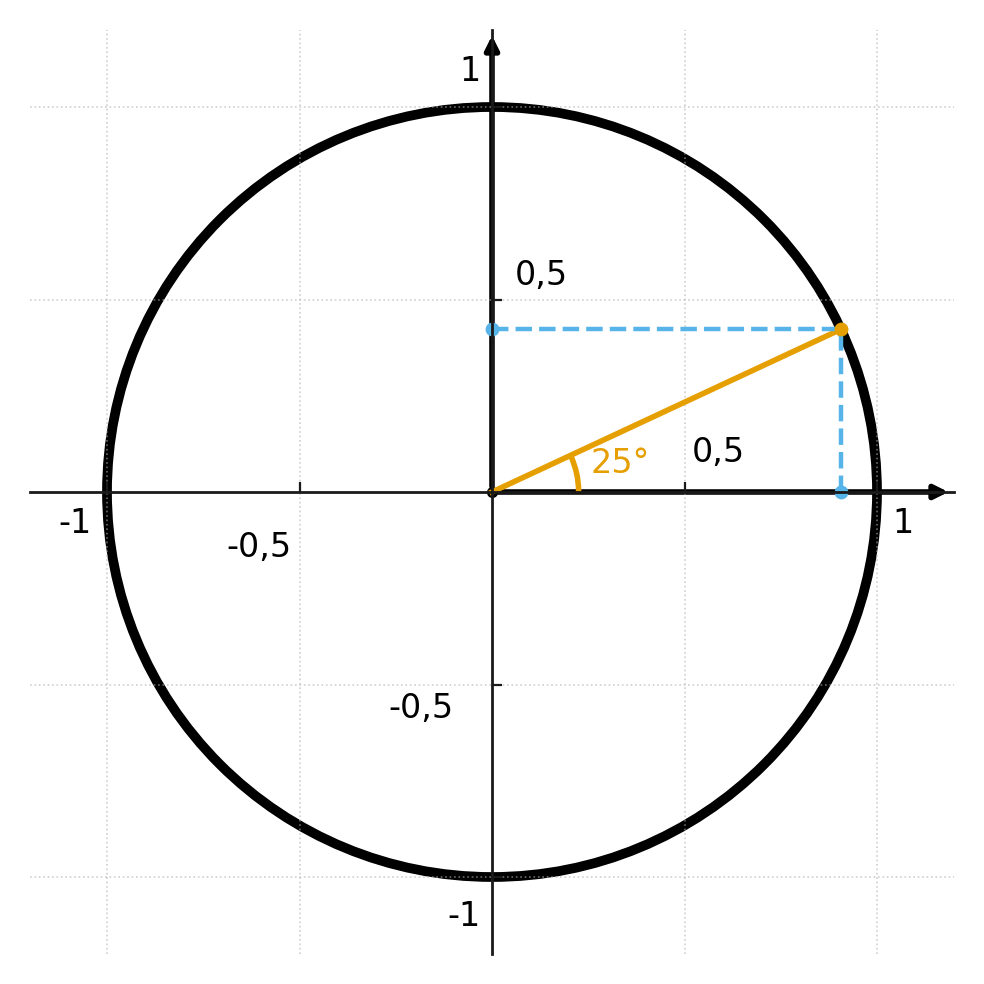
Denken Sie daran, dass Koordinaten immer als \( \large (x,y) \) gelesen werden, was \( \large (Kosinus, Sinus) \) entspricht.

Kosinus und Sinus sind also das Koordinatenpaar des Referenzpunktes – des Punktes, an dem der Winkel den Einheitskreis schneidet.

Der Winkel in der Abbildung beträgt 25 Grad, und wenn man ihn genau genug ablesen könnte, würde man sehen, dass:

 

$$ sin(v) \approx 0.906 $$

$$ cos(v) \approx 0.423 $$

 

Natürlich ist es nicht möglich, exakt am Einheitskreis abzulesen, und normalerweise verwendet man die Kosinus- und Sinus-Tasten auf dem Taschenrechner.

 

Inverse Funktionen

Wenn man den Kosinus oder Sinus eines Winkels kennt, aber nicht den Winkel selbst, kann man mit den inversen Funktionen in die andere Richtung rechnen. Diese heißen arccos und arcsin (oder werden als cos^-1 und sin^-1 geschrieben).

Die inversen Funktionen finden sich ebenfalls auf einem Taschenrechner, in der Regel auf derselben Taste wie die normalen Funktionen.

 

Nehmen wir an, Sie wissen, dass cos(A) = 0.906, den Winkel aber nicht. Dann können Sie ihn so berechnen:

 

$$ cos^{-1}(0.906) \approx 25^\circ $$

 

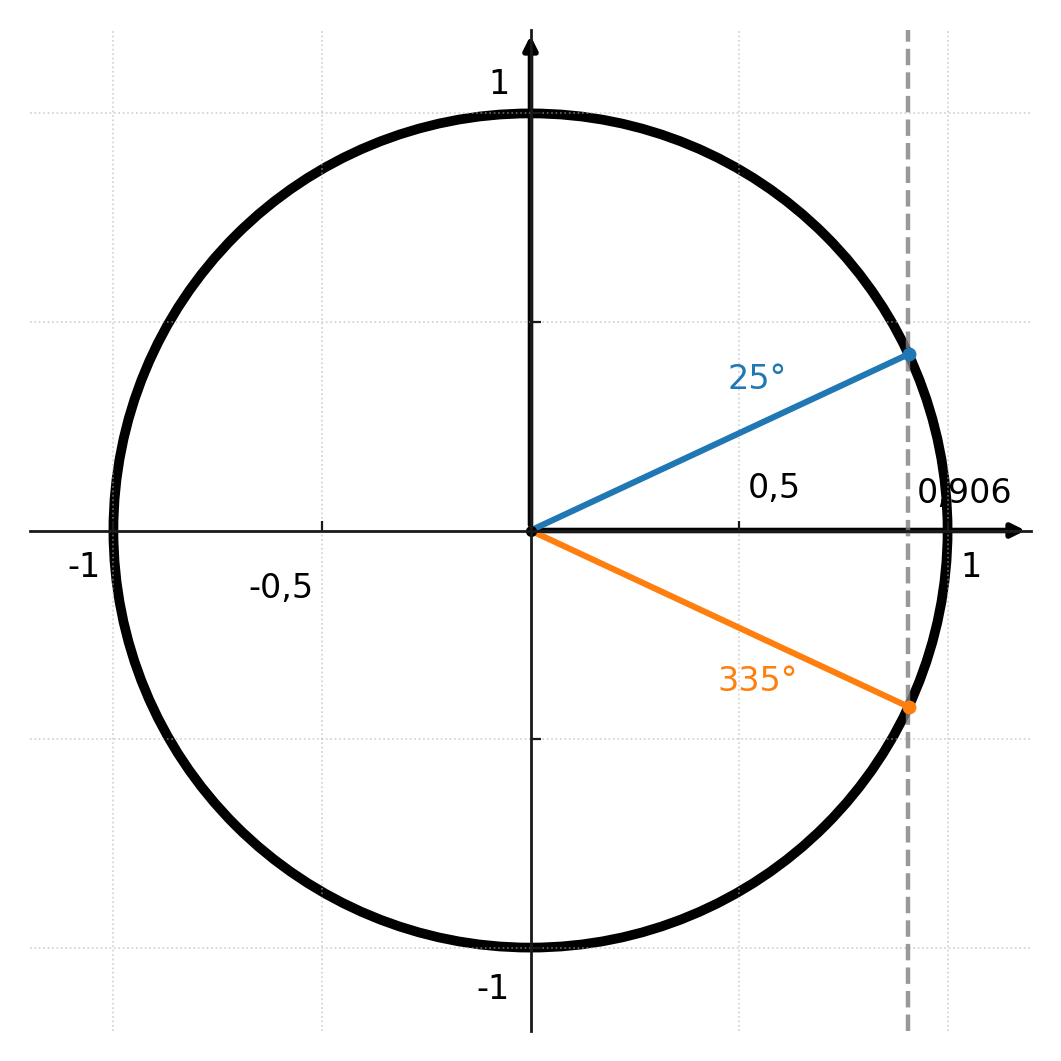
Beachten Sie, dass die inversen Funktionen nicht immer eine eindeutige Lösung liefern. Zum Beispiel kann cos(v) = 0.906 sowohl für einen Winkel von 25° als auch für einen Winkel von 335° (-25°) gelten.

Damit die Funktionen als eindeutige inverse Funktionen verwendet werden können, wird ihre Definition eingeschränkt:

 

• Arccos ist normalerweise auf das Intervall \(0^\circ \leq v \leq 180^\circ\) (\(0 \leq v \leq \pi\) rad) beschränkt
• Arcsin ist normalerweise auf das Intervall \(-90^\circ \leq v \leq 90^\circ\) (\(-\tfrac{\pi}{2} \leq v \leq \tfrac{\pi}{2}\) rad) beschränkt

 

Das bedeutet, dass die Lösung bei 335° nicht erscheint und dass arcsin immer Winkel im ersten oder vierten Quadranten zurückgibt.

 

 

 

 

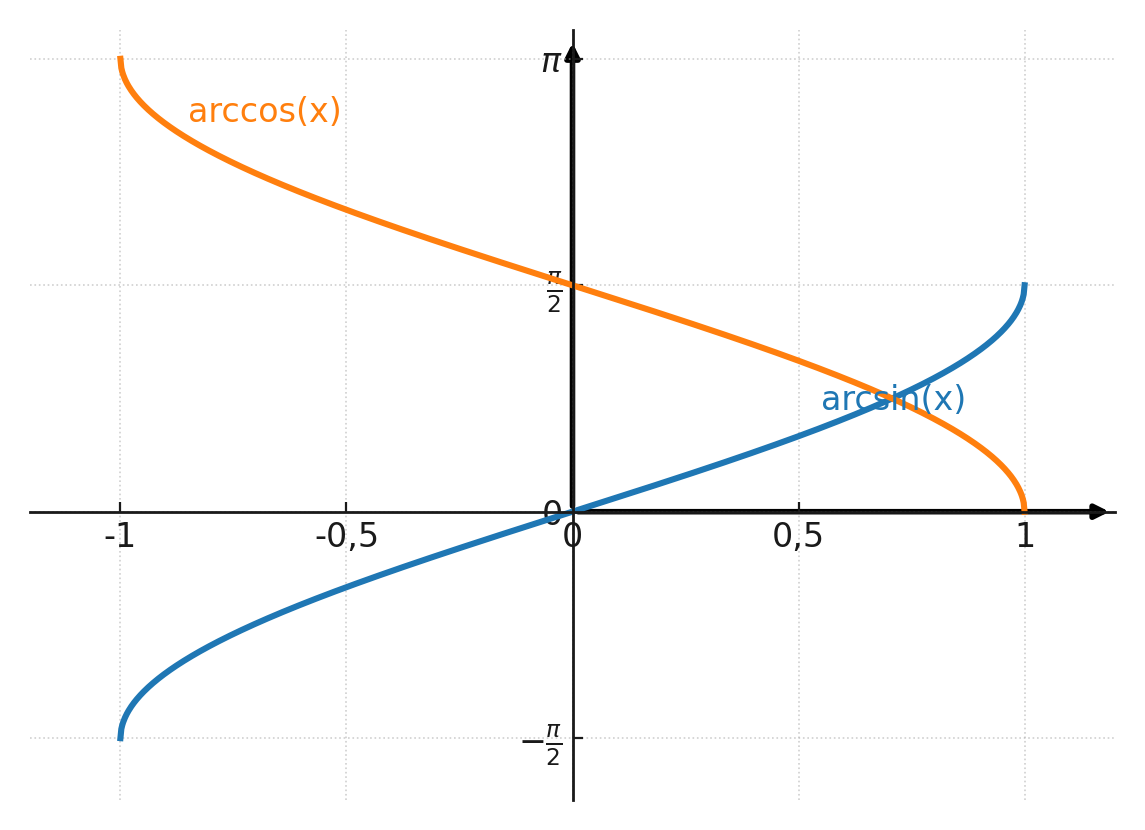
Die beiden inversen Funktionen sind im Koordinatensystem eingezeichnet. Beachten Sie, dass die y-Achse in Radiant und nicht in Grad angegeben ist.

Wenn man auf der arccos-Kurve bei x = 0.906 abliest, erhält man 0.44 rad, was 25° entspricht.

 

 

 

Radiant und Grad

Um zwischen Radiant und Grad zu konvertieren, verwendet man die Formel:

 

$$ \text{Grad} = \text{Radiant} \cdot \frac{180^\circ}{\pi} $$

$$ \text{Radiant} = \text{Grad} \cdot \frac{\pi}{180^\circ} $$

 

Beispiel:

 

$$ 0.44 \,\text{rad} \approx 0.44 \cdot \tfrac{180^\circ}{\pi} \approx 25^\circ $$