Bestimmtes Integral

Das bestimmte Integral wird verwendet, um die Gesamtgröße einer Funktion zwischen zwei Punkten zu berechnen. Während das unbestimmte Integral alle Stammfunktionen beschreibt, liefert das bestimmte Integral eine Zahl, die den akkumulierten Wert darstellt — oft eine Fläche.

 

 

Definition

Das bestimmte Integral einer Funktion \( \large f(x) \) von \( \large a \) bis \( \large b \) wird als Grenzwert der Summe vieler kleiner Rechtecke unter der Kurve definiert:

 

$$ \large \int_a^b f(x)\,dx \;=\; \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i)\,\Delta x $$

 

Jeder Summand stellt die Fläche eines kleinen Rechtecks mit der Höhe \( \large f(x_i) \) und der Breite \( \large \Delta x \) dar. Wenn die Anzahl der Rechtecke zunimmt, wird die Näherung immer genauer, und im Grenzwert erhält man die exakte Fläche.

 

 

Geometrische Interpretation

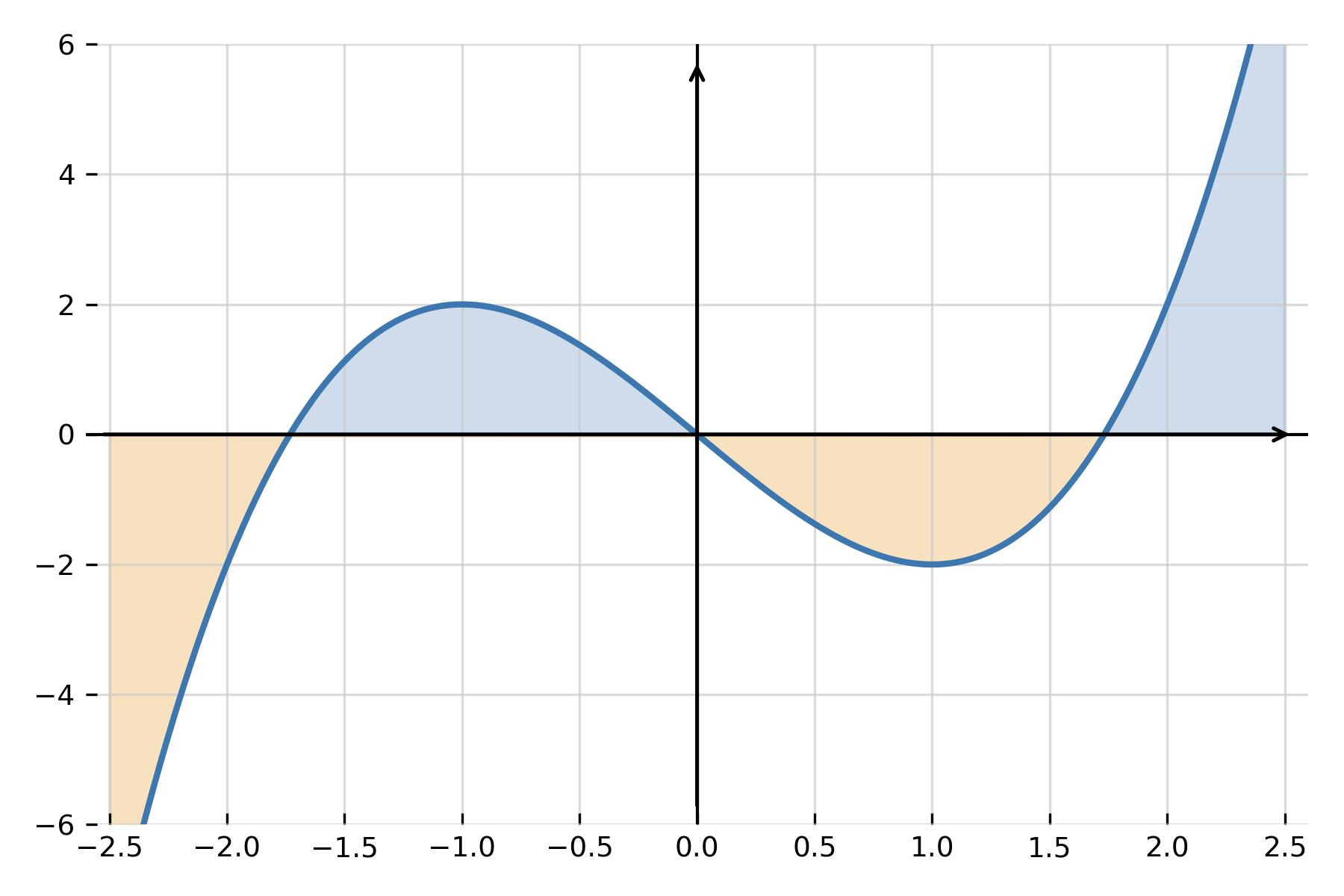
Wenn \( \large f(x) \ge 0 \) im Intervall gilt, stellt das bestimmte Integral die Fläche zwischen der Kurve und der x-Achse dar. Schneidet die Funktion die x-Achse, werden die Bereiche unter der Achse negativ gezählt, sodass das Integral die Nettosumme der Flächen angibt.

 

 

 

Fundamentalsatz

Es besteht ein enger Zusammenhang zwischen Stammfunktionen und bestimmten Integralen. Wenn \( \large F \) eine Stammfunktion von \( \large f \) ist, gilt der fundamentale Satz der Integralrechnung:

 

$$ \large \int_a^b f(x)\,dx \;=\; F(b) - F(a) $$

 

Das bedeutet, dass man ein bestimmtes Integral berechnen kann, ohne Riemann-Summen zu bilden. Stattdessen findet man eine Stammfunktion und subtrahiert die Funktionswerte an den beiden Grenzen.

 

 

Beispiel 1: Fläche unter der Kurve

Finde die Fläche unter \( \large f(x) = x^2 \) von \( \large x=0 \) bis \( \large x=3 \):

 

$$ \large \int_0^3 x^2\,dx \;=\; \Big[\tfrac{1}{3}x^3\Big]_0^3 \;=\; \tfrac{1}{3}\cdot 27 - 0 \;=\; 9 $$

 

Die Fläche unter der Kurve beträgt also 9 Einheiten.

 

 

Beispiel 2: Negative und positive Beiträge

Finde \( \large \int_{-1}^{2} (x-1)\,dx \):

 

$$ \large \int_{-1}^{2} (x-1)\,dx \;=\; \Big[\tfrac{1}{2}x^2 - x\Big]_{-1}^{2} \;=\; \big(2 - 2\big) - \big(\tfrac{1}{2} - (-1)\big) = -\tfrac{3}{2} $$

 

Das Integral ist negativ, weil die Funktion in einem Teil des Intervalls unter der x-Achse liegt. Das bestimmte Integral misst also die Nettosumme, nicht nur die Summe der positiven Flächen.

 

 

Vorzeichen und akkumulierte Größe

Ein positives Integral bedeutet, dass die Funktion im Durchschnitt über der x-Achse liegt. Ein negatives Integral bedeutet das Gegenteil. In der Physik und der Ökonomie wird dies als Überschuss oder Defizit einer Gesamtmenge interpretiert.

 

 

Grafische Interpretation

Das bestimmte Integral kann als Summe der mit Vorzeichen versehenen Flächen verstanden werden. Es kann daher als die Fläche zwischen der Kurve und der x-Achse visualisiert werden, wobei die unter der Achse liegenden Flächen abgezogen werden.

 

 

Zusammenfassung

Das bestimmte Integral liefert eine Zahl, die die gesamte Änderung, die akkumulierte Menge oder die Nettofläche einer Funktion zwischen zwei Grenzen darstellt. Es kann entweder geometrisch als Fläche oder algebraisch über Stammfunktionen und den fundamentalen Satz gefunden werden.