Anwendungen der Integralrechnung
Integrale werden nicht nur verwendet, um Flächen zu berechnen, sondern auch in vielen verschiedenen Zusammenhängen, in denen man kleine Beiträge summieren muss, um eine Gesamtgröße zu erhalten. In Physik, Wirtschaft und Geometrie bieten Integrale ein präzises mathematisches Werkzeug, um das gesamte Wachstum, die Energie, die Masse, die Entfernung oder das Volumen zu messen.
Fläche zwischen zwei Kurven
Eine der häufigsten Anwendungen besteht darin, die Fläche zwischen zwei Funktionen \( \large f(x) \) und \( \large g(x) \) zu bestimmen. Wenn \( \large f(x) \ge \large g(x) \) im Intervall \([ \large a,\large b ]\), wird die Fläche als Differenz zwischen beiden berechnet:
$$ \large A \;=\; \int_a^b \big(f(x) - g(x)\big)\,dx $$
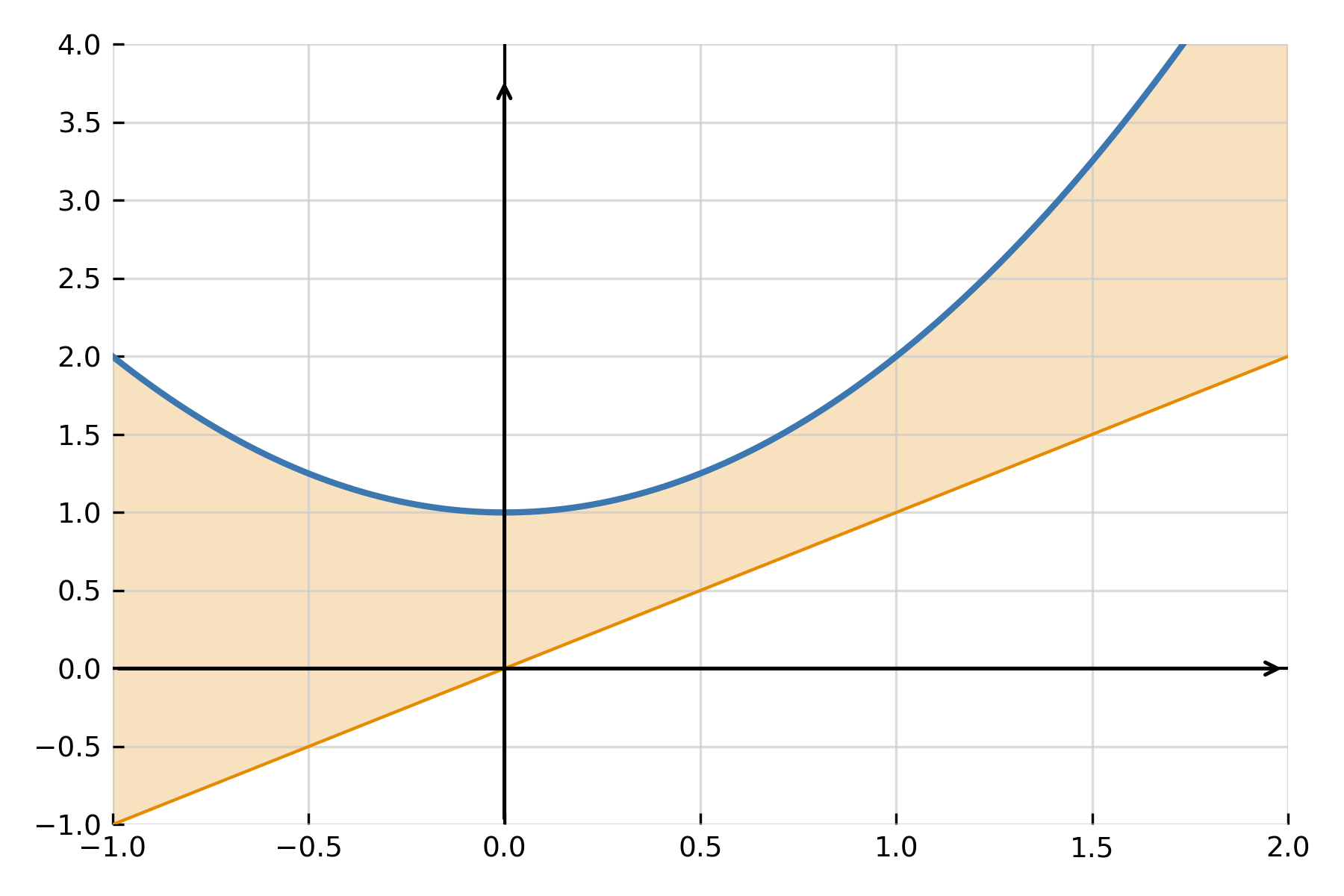
Das Integral misst genau den vertikalen Abstand zwischen den Kurven für jedes \( \large x \) und summiert ihn über das Intervall. Wenn sich die Graphen schneiden, wird das Intervall in Abschnitte unterteilt, wobei jeweils die positive Differenz genommen wird.
Volumen von Rotationskörpern
Wenn eine Funktion um die x-Achse gedreht wird, entsteht ein dreidimensionaler Körper. Das Volumen kann bestimmt werden, indem man die Querschnittsflächen (Kreisscheiben) entlang der Achse aufsummiert:
$$ \large V \;=\; \pi \int_a^b \big(f(x)\big)^2\,dx $$
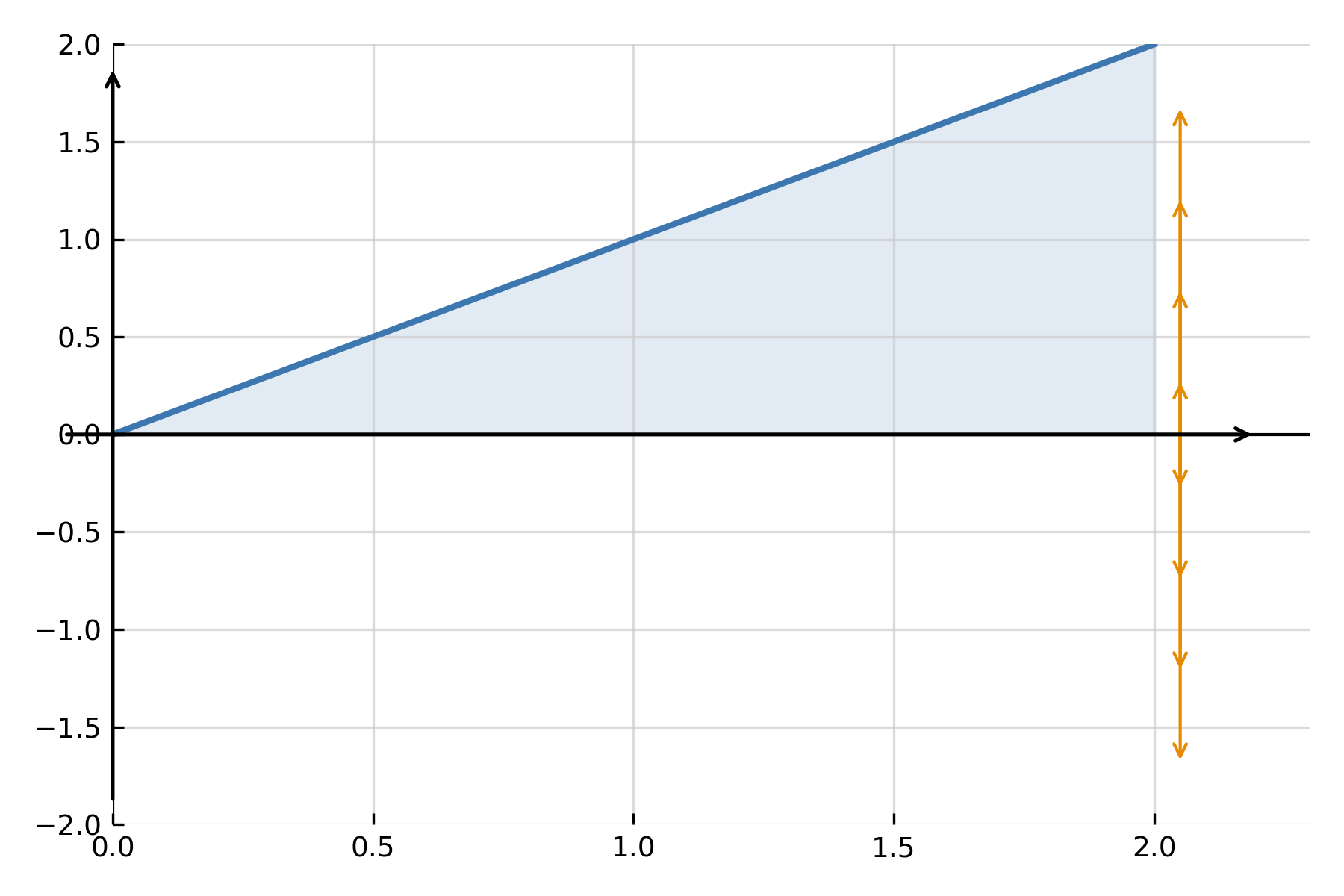
Hier ist \( \large f(x) \) der Radius der gedrehten Funktion an der Stelle \( \large x \). Das Integral summiert unendlich viele kleine Kreisscheiben, die zusammen das Gesamtvolumen bilden.
Beispiel: Rotationskörper
Bestimme das Volumen des Körpers, der entsteht, wenn \( \large f(x)=x \) um die x-Achse von \( \large x=0 \) bis \( \large x=2 \) rotiert:
$$ \large V \;=\; \pi \int_0^2 x^2\,dx \;=\; \pi \Big[\tfrac{1}{3}x^3\Big]_0^2 \;=\; \tfrac{8}{3}\pi $$
Dies entspricht dem Volumen eines Kegels mit der Höhe 2 und dem Radius 2.
Arbeit und Energie
In der Physik werden Integrale verwendet, um Arbeit zu berechnen, wenn eine Kraft von der Position abhängt. Die Arbeit \( \large W \) ist die Summe kleiner Kraftanteile \( \large F(x)\,dx \):
$$ \large W \;=\; \int_a^b F(x)\,dx $$
Wenn die Kraft konstant ist, reduziert sich dies auf \( \large W = F \cdot s \), doch das Integral ermöglicht die Berechnung, wenn sich die Kraft entlang der Bewegung ändert.
Bewegung und zurückgelegte Strecke
Wenn die Geschwindigkeitsfunktion \( \large v(t) \) eines Körpers bekannt ist, ergibt das Integral von \( \large v(t) \) die zurückgelegte Strecke:
$$ \large s \;=\; \int_{t_1}^{t_2} v(t)\,dt $$
Wenn die Geschwindigkeit negativ sein kann (Rückwärtsbewegung), muss mit Vorzeichen integriert werden. Wenn man die gesamte Strecke unabhängig von der Richtung möchte, verwendet man \( \large \int |v(t)|\,dt \).
Wirtschaftliche und biologische Anwendungen
Integrale werden auch verwendet, um das akkumulierte Wachstum, den Verbrauch oder den Ertrag über die Zeit zu berechnen. In der Wirtschaft kann \( \large f(x) \) eine Grenzfunktion darstellen, z. B. den Ertrag pro Einheit, und das Integral liefert den Gesamtertrag. In der Biologie werden Integrale verwendet, um die Gesamtbiomasse, die Energieaufnahme oder die Stoffmenge einer Population zu bestimmen.
Durchschnittswert einer Funktion
Der Durchschnittswert einer Funktion in einem Intervall wird berechnet, indem man die Gesamtfläche nimmt und sie durch die Länge des Intervalls teilt:
$$ \large f_{\text{avg}} \;=\; \frac{1}{b-a}\int_a^b f(x)\,dx $$
Diese Formel wird in Statistik, Physik und Analysis verwendet, um Mittelwerte kontinuierlicher Funktionen zu finden.
Wenn ein Integral nicht analytisch berechnet werden kann, kann man stattdessen numerische Methoden wie die Rechteckmethode, die Trapezmethode oder die Simpson-Regel verwenden, um einen Näherungswert zu bestimmen. Diese Methoden werden im Abschnitt Numerische Methoden beschrieben.
Zusammenfassung
Integrale werden verwendet, um Flächen, Volumen, Energie, Arbeit und vieles mehr zu berechnen. Allen Anwendungen ist gemeinsam, dass das Integral kleine Teile zu einer Gesamtgröße aufsummiert. Damit bildet die Integralrechnung ein zentrales Werkzeug zur Beschreibung und Berechnung von Zusammenhängen in Natur, Technik und Wirtschaft.