Integralrechnung

Die Integralrechnung befasst sich damit, kleine Beiträge zusammenzuzählen, um eine gesamte Größe zu erhalten. Während die Differentialrechnung momentane Änderungen (\( \large \text{Steigungen} \)) misst, misst die Integralrechnung akkumulierte Größen wie Fläche, Wegstrecke, Wachstum oder Energie. Beide Bereiche hängen eng zusammen: Differenzieren und Integrieren sind umgekehrte Prozesse.

 

 

Was ist Integralrechnung

Wenn sich eine Größe allmählich verändert, kann man sich vorstellen, den Prozess in viele kleine Teile zu zerlegen und sie zu addieren. Das ist das Wesen der Integralrechnung: Die Summe vieler „kleiner Stücke“ ergibt eine Gesamtgröße. In der Praxis wird dies durch Integrale ausgedrückt.

 

 

Geometrische Deutung

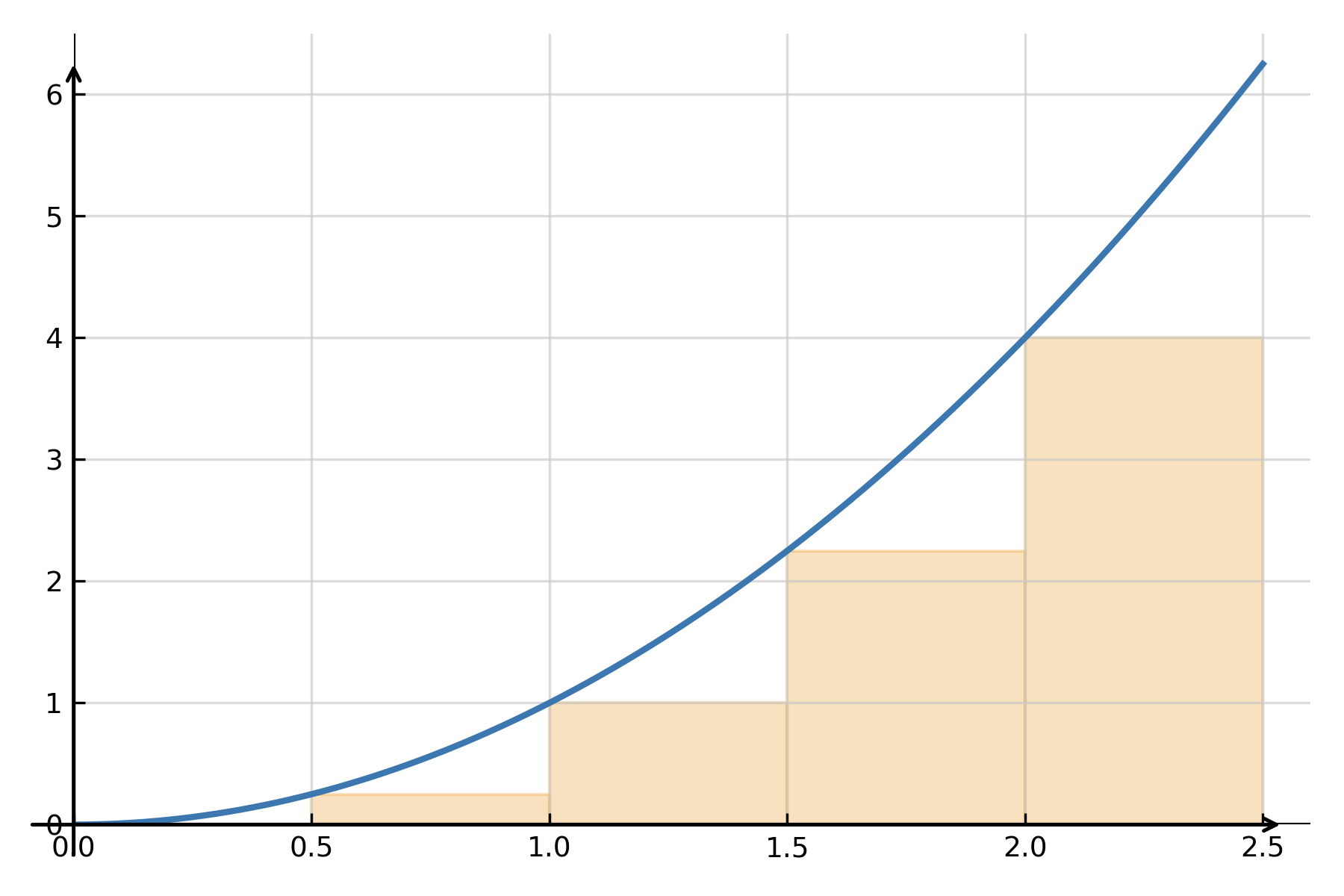
Eine klassische Deutung ist die Fläche unter dem Graphen einer nichtnegativen Funktion \( \large f(x) \) zwischen \( \large x=a \) und \( \large x=b \). Die Fläche kann angenähert werden, indem man das Intervall in schmale Rechtecke teilt, ihre Flächen berechnet und sie addiert. Wenn die Breite gegen null geht, nähert sich die Summe der exakten Fläche.

 

$$ \large \text{Fläche} \;=\; \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i)\,\Delta x \;=\; \int_a^b f(x)\,dx $$

 

Das Integral liefert also eine präzise Methode, eine „akkumulierte Größe“ zu messen, sei es Fläche, Masse, Arbeit oder eine andere physikalische Größe.

 

 

 

Unbestimmtes Integral (Stammfunktion)

Das unbestimmte Integral stellt die „umgekehrte Ableitung“ dar. Wenn \( \large F'(x)=f(x) \), dann nennt man \( \large F \) eine Stammfunktion von \( \large f \), und man schreibt:

 

$$ \large \int f(x)\,dx \;=\; F(x) + C $$

 

Hier ist \( \large C \) eine beliebige Konstante. Das unbestimmte Integral beschreibt alle Funktionen, die dieselbe Ableitung \( \large f \) besitzen.

 

 

Bestimmtes Integral (Fläche und Summe)

Das bestimmte Integral misst die akkumulierte Größe zwischen zwei Grenzen \( \large a \) und \( \large b \). Es wird als Grenzwert der Riemann-Summen definiert:

 

$$ \large \int_a^b f(x)\,dx \;=\; \lim_{n\to\infty}\sum_{i=1}^{n} f(x_i)\,\Delta x $$

 

Wenn \( \large f \ge 0 \) im Intervall ist, stellt dies die Fläche unter dem Graphen dar. Wenn \( \large f \) das Vorzeichen wechselt, wird die Fläche unter der x-Achse negativ gezählt, was die Nettoakkumulation widerspiegelt.

 

 

Zusammenhang mit der Differentialrechnung (Fundamentalsatz)

Die Integral- und Differentialrechnung sind durch den Fundamentalsatz der Analysis verknüpft: Wenn \( \large f \) auf \( \large [a,b] \) stetig ist und \( \large F \) eine Stammfunktion von \( \large f \) ist, dann gilt:

 

$$ \large \int_a^b f(x)\,dx \;=\; F(b) - F(a) $$

 

Das bedeutet, dass eine Fläche (eine Summe) mit Hilfe einer Stammfunktion berechnet werden kann und dass Differenzieren und Integrieren umgekehrte Prozesse sind.

 

 

Beispiele

1. Fläche unter einer einfachen Funktion

Berechne \( \large \int_0^2 x\,dx \). Eine Stammfunktion ist \( \large F(x)=\tfrac{1}{2}x^2 \), also:

 

$$ \large \int_0^2 x\,dx \;=\; \Big[\tfrac{1}{2}x^2\Big]_0^2 \;=\; \tfrac{1}{2}\cdot 4 - 0 \;=\; 2 $$

 

2. Zurückgelegter Weg aus einer Geschwindigkeitsfunktion

Wenn die Geschwindigkeit eines Autos \( \large v(t)=3t \) (m/s) beträgt, dann ist die zurückgelegte Strecke von \( \large t=0 \) bis \( \large t=4 \):

 

$$ \large s \;=\; \int_0^4 v(t)\,dt \;=\; \int_0^4 3t\,dt \;=\; \Big[\tfrac{3}{2}t^2\Big]_0^4 \;=\; 24\ \text{m} $$

 

Dies zeigt, dass die Fläche unter der Geschwindigkeitskurve der insgesamt zurückgelegten Strecke entspricht.

 

 

Warum zwei Arten von Integralen

Das unbestimmte Integral (Stammfunktion) ist ein Werkzeug zur algebraischen Bestimmung von Formeln, während das bestimmte Integral \( \large \text{eine konkrete Größe misst} \) — also eine Fläche oder eine Summe über ein Intervall. Der Fundamentalsatz ermöglicht die Verbindung zwischen diesen beiden Sichtweisen.

 

 

Zusammenfassung

Die Integralrechnung befasst sich mit dem Aufsummieren kleiner Beiträge zu einer Gesamtgröße. Geometrisch werden Integrale als Flächen interpretiert; physikalisch als akkumulierte Masse, Arbeit oder Wegstrecke. Mit dem Fundamentalsatz können bestimmte Integrale mithilfe von Stammfunktionen berechnet werden, wodurch die Integralrechnung als natürlicher „umgekehrter“ Prozess der Differentialrechnung erscheint.