Newton-Raphson

El método de Newton-Raphson es una técnica numérica rápida para encontrar raíces de una función, es decir, puntos donde $ \large f(x) = 0 $. El método utiliza tanto el valor de la función como su derivada para mejorar la estimación de la posición de la raíz.

Idea del método

El punto de partida es una suposición inicial $ \large x_0 $. En el punto $ \large (x_0, f(x_0)) $ se traza la tangente a la curva. El punto donde esta tangente corta el eje x se utiliza como nueva estimación $ \large x_1 $. El proceso se repite hasta que la diferencia entre dos estimaciones consecutivas sea menor que una tolerancia elegida $ \large \varepsilon $.

Fórmula

$$ \large x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} $$

Procedimiento paso a paso

Elegir un punto inicial $ \large x_0 $.
Calcular $ \large f(x_0) $ y $ \large f'(x_0) $.
Usar la fórmula para encontrar $ \large x_1 $.
Repetir hasta que $ \large |x_{n+1} - x_n| < \varepsilon $.

Ejemplo

Queremos encontrar la raíz de $ \large f(x) = x^3 - x - 2 $, que ya resolvimos anteriormente con el método de bisección.

La derivada es $ \large f'(x) = 3x^2 - 1 $.

Elegimos una estimación inicial $ \large x_0 = 1{,}5 $.

$$ \large f(1{,}5) = (1{,}5)^3 - 1{,}5 - 2$$

$$ \large f(1{,}5) = -0{,}125 $$

$$ \large f'(1{,}5) = 3(1{,}5)^2 - 1 $$

$$ \large f'(1{,}5) = 5{,}75 $$

$$ \large x_1 = 1{,}5 - \frac{-0{,}125}{5{,}75} $$

$$ \large x_1 = 1{,}5217 $$

Después de pocas iteraciones, el método converge rápidamente hacia la raíz $ \large x \approx 1{,}521 $.

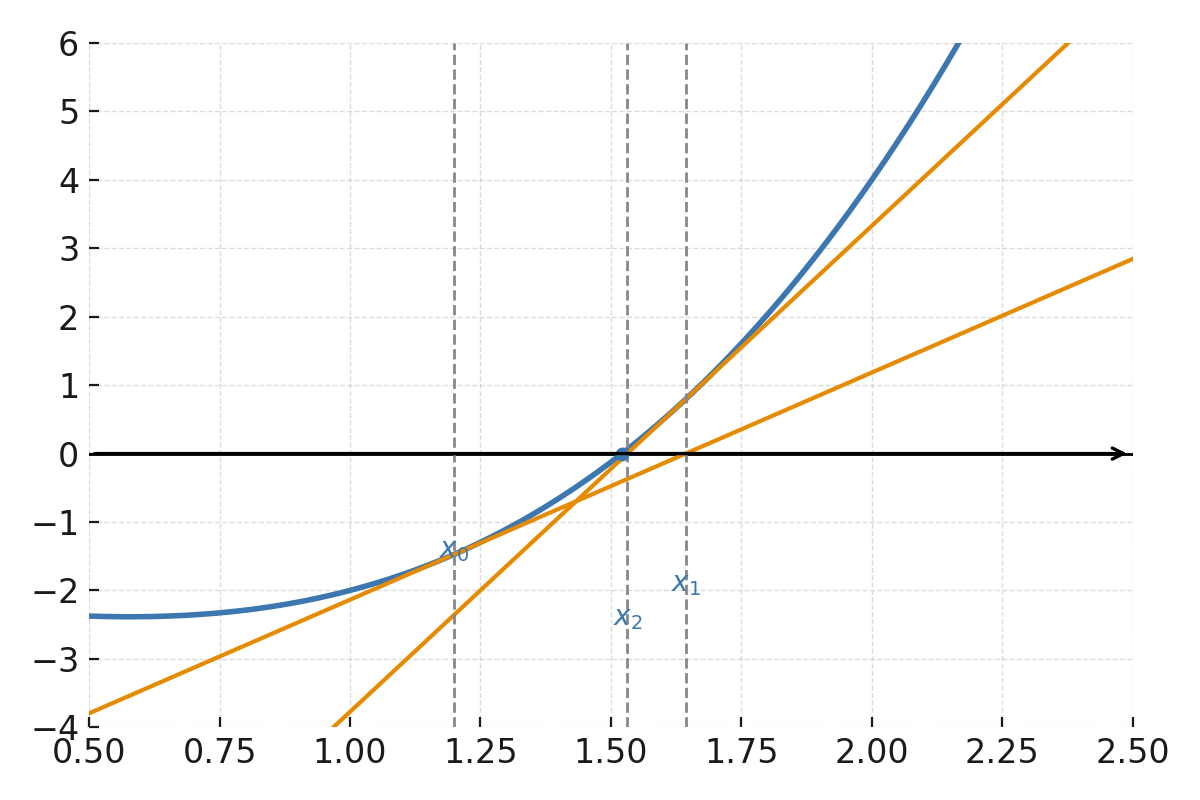
Método de Newton-Raphson

La función $ \large f(x) = x^3 - x - 2 $. La estimación inicial $ \large x_0 $ está marcada en el eje x, y la tangente en $ \large x_0 $ se muestra como una línea que corta el eje x en $ \large x_1 $. Luego se traza la tangente en $ \large x_1 $, que corta el eje x aún más cerca de la raíz. La figura ilustra la mejora iterativa.

Observaciones

El método de Newton-Raphson converge mucho más rápido que el método de bisección, pero requiere que la derivada $ \large f'(x) $ pueda calcularse y que la estimación inicial esté cerca de la raíz real. Si la tangente es casi horizontal (es decir, $ \large f'(x) \approx 0 $), el método puede fallar o sobrepasar la raíz.