Método de bisección

El método de bisección es una técnica numérica sencilla para encontrar una raíz en una función continua, es decir, un punto donde $ \large f(x) = 0 $.

El método se basa en el teorema del valor intermedio, que establece que si $ \large f(a) $ y $ \large f(b) $ tienen signos opuestos, debe existir al menos una raíz en el intervalo $ \large [a,b] $.

Idea del método

El intervalo se divide repetidamente en dos mitades. En cada paso, se determina en cuál mitad la función cambia de signo. Esa mitad se elige como el nuevo intervalo, y el proceso se repite hasta que la posición de la raíz se conoce con la precisión deseada.

Procedimiento paso a paso

Elegir un intervalo inicial $ \large [a,b] $ donde $ \large f(a) $ y $ \large f(b) $ tengan signos opuestos.
Calcular el punto medio $ \large m = \frac{a + b}{2} $.
Evaluar $ \large f(m) $.
Si $ \large f(m) = 0 $ (o muy cercano a 0), entonces $ \large m $ es la raíz.
De lo contrario, si $ \large f(a) $ y $ \large f(m) $ tienen signos opuestos, establecer $ \large b = m $; de lo contrario, establecer $ \large a = m $.
Repetir los pasos 2–5 hasta que la longitud del intervalo sea menor que la tolerancia elegida $ \large \varepsilon $.

Ejemplo

Queremos encontrar la raíz de la función $ \large f(x) = x^3 - x - 2 $.

Observamos que $ \large f(1) = -2 $ y $ \large f(2) = 4 $, por lo tanto, la función cambia de signo en el intervalo $ \large [1,2] $.

$$ \large m_1 = \frac{1 + 2}{2} = 1{,}5 $$

$$ \large f(1{,}5) = (1{,}5)^3 - 1{,}5 - 2 $$

$$ \large f(1{,}5) = -0{,}125 $$

Como $ \large f(1{,}5) $ y $ \large f(2) $ tienen signos opuestos, se elige un nuevo intervalo $ \large [1{,}5, 2] $.

$$ \large m_2 = \frac{1{,}5 + 2}{2} = 1{,}75 $$

$$ \large f(1{,}75) = (1{,}75)^3 - 1{,}75 - 2 $$

$$ \large f(1{,}75) = 1{,}609 - 3{,}75 $$

$$ \large f(1{,}75) = -0{,}109 $$

El proceso se repite hasta que $ \large a $ y $ \large b $ estén tan cerca que se pueda leer la raíz como $ \large x \approx 1{,}521 $.

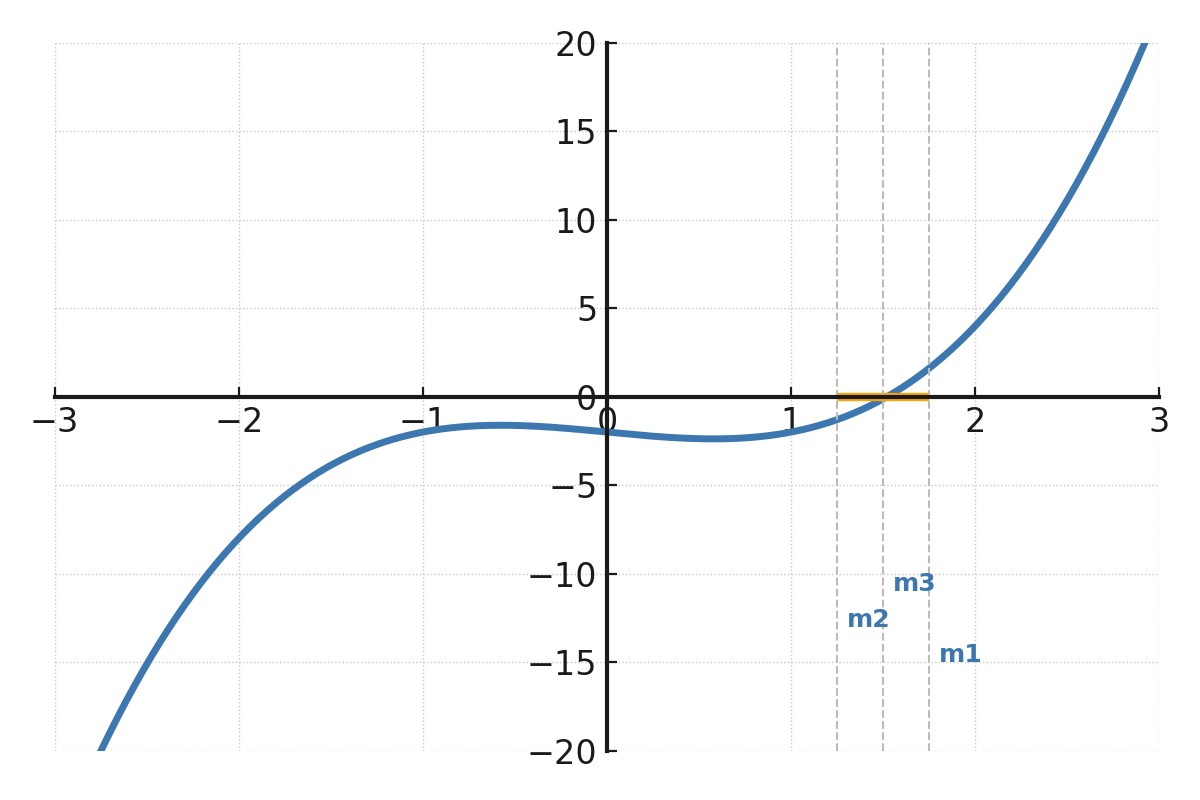
Método de bisección

La función $ \large f(x) = x^3 - x - 2 $, donde el intervalo $ \large [1,2] $ está marcado con una línea en el eje x.

Los puntos medios $ \large m_1, m_2, m_3 $ se muestran como líneas verticales que se acercan gradualmente a la posición de la raíz, donde la gráfica cruza el eje x.

Nota

El método de bisección es muy robusto, ya que siempre converge si la función es continua y cambia de signo. La desventaja es que converge lentamente en comparación con métodos más avanzados como Newton-Raphson.