Regla del trapecio

El método del trapecio es un procedimiento numérico sencillo para calcular un valor aproximado de una integral definida. Se basa en la idea de reemplazar la gráfica de una función por líneas rectas, de modo que el área bajo la curva pueda calcularse como la suma de trapecios.

 

 

Idea del método

Cuando no se puede encontrar la integral exacta \( \large \int_a^b f(x)\,dx \), el intervalo \( \large [a,b] \) puede dividirse en \( \large n \) subintervalos más pequeños. En cada subintervalo, la función se reemplaza por una línea recta entre los dos extremos. El área bajo esta línea es un trapecio, fácil de calcular.

 

 

Fórmula del método del trapecio

Para un intervalo dividido en \( \large n \) partes iguales con anchura \( \large h = \frac{b-a}{n} \), se cumple:

 

$$ \large \int_a^b f(x)\,dx \approx \frac{h}{2} \left[f(x_0) + 2f(x_1) + 2f(x_2) + \ldots + 2f(x_{n-1}) + f(x_n)\right] $$

 

 

Procedimiento paso a paso

 

1. Dividir el intervalo \( \large [a,b] \) en \( \large n \) partes iguales.
2. Calcular \( \large h = \frac{b-a}{n} \).
3. Calcular los valores de la función \( \large f(x_0), f(x_1), \ldots, f(x_n) \).
4. Sustituir los valores en la fórmula del trapecio.

 

 

Ejemplo

Calcularemos el área aproximada bajo la función \( \large f(x) = x^2 \) en el intervalo \( \large [0,2] \) utilizando 4 trapecios.

 

Aquí \( \large a = 0 \), \( \large b = 2 \) y \( \large n = 4 \), por lo tanto \( \large h = \frac{2-0}{4} = 0{,}5 \).

 

Los valores de la función son:

 

$$ \large f(0)=0, \quad f(0{,}5)=0{,}25, \quad f(1)=1, \quad f(1{,}5)=2{,}25, \quad f(2)=4 $$

 

La fórmula del trapecio da:

 

$$ \large A \approx \frac{0{,}5}{2}\,[0 + 2(0{,}25 + 1 + 2{,}25) + 4] = 2{,}75 $$

 

La integral exacta es \( \large \int_0^2 x^2\,dx = \frac{8}{3} \approx 2{,}67 \), por lo que el método proporciona una buena aproximación.

 

 

 

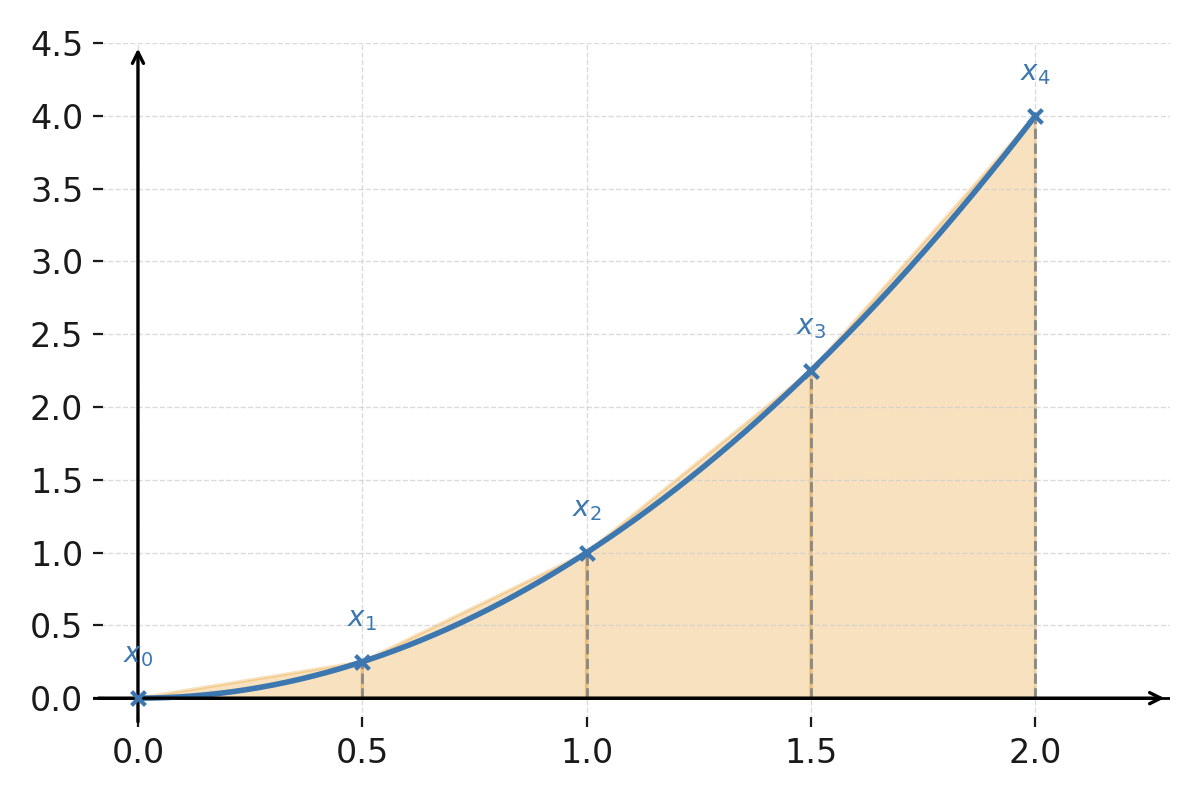
La función \( \large f(x) = x^2 \) en el intervalo \( \large [0,2] \).

Los cuatro subintervalos están marcados con líneas verticales discontinuas, y los trapecios correspondientes se muestran entre la curva y el eje x.

 

 

Observaciones

El método del trapecio es fácil de implementar y suele proporcionar buena precisión, pero puede subestimar o sobrestimar el área dependiendo de si la función es convexa o cóncava. La precisión puede mejorarse utilizando más subintervalos o aplicando la regla de Simpson.