Regla de Simpson
La regla de Simpson es una mejora del método del trapecio para calcular numéricamente una integral definida. Mientras que el método del trapecio sustituye la función por líneas rectas, la regla de Simpson utiliza parábolas (polinomios cuadráticos) para aproximar la curva. Esto proporciona una mayor precisión incluso con pocos subintervalos.
Idea del método
Supongamos que queremos calcular el área bajo la función \( \large f(x) \) entre \( \large a \) y \( \large b \). El intervalo se divide en un número par de subintervalos (por ejemplo \( \large n = 4 \)). En cada par de subintervalos se traza una parábola que pasa por los tres puntos \( \large (x_{2i}, f(x_{2i})) \), \( \large (x_{2i+1}, f(x_{2i+1})) \) y \( \large (x_{2i+2}, f(x_{2i+2})) \). La suma de las áreas bajo estas parábolas da una aproximación de la integral total.
Fórmula de la regla de Simpson
Si \( \large n \) es un número par y el ancho de los subintervalos es \( \large h = \frac{b-a}{n} \), entonces:
$$ \large \int_a^b f(x)\,dx \approx \frac{h}{3}\,[f(x_0) + 4f(x_1) + 2f(x_2) + 4f(x_3) + \ldots + 4f(x_{n-1}) + f(x_n)] $$
Procedimiento paso a paso
- Dividir el intervalo \( \large [a,b] \) en un número par de subintervalos \( \large n \).
- Calcular \( \large h = \frac{b-a}{n} \).
- Calcular los valores de la función \( \large f(x_0), f(x_1), \ldots, f(x_n) \).
- Sustituir los valores en la fórmula de Simpson.
Ejemplo
Calculamos el área aproximada bajo \( \large f(x) = x^2 \) en el intervalo \( \large [0,2] \) con \( \large n = 4 \).
Aquí \( \large h = \frac{2-0}{4} = 0{,}5 \).
Los valores de la función son:
$$ \large f(0)=0, \quad f(0{,}5)=0{,}25, \quad f(1)=1, \quad f(1{,}5)=2{,}25, \quad f(2)=4 $$
Sustituyendo en la fórmula de Simpson obtenemos:
$$ \large A \approx \frac{0{,}5}{3}\,[0 + 4(0{,}25) + 2(1) + 4(2{,}25) + 4] = 2{,}67 $$
Esto corresponde exactamente a la integral exacta:
$$ \large \int_0^2 x^2\,dx = \frac{8}{3} = 2{,}67 $$
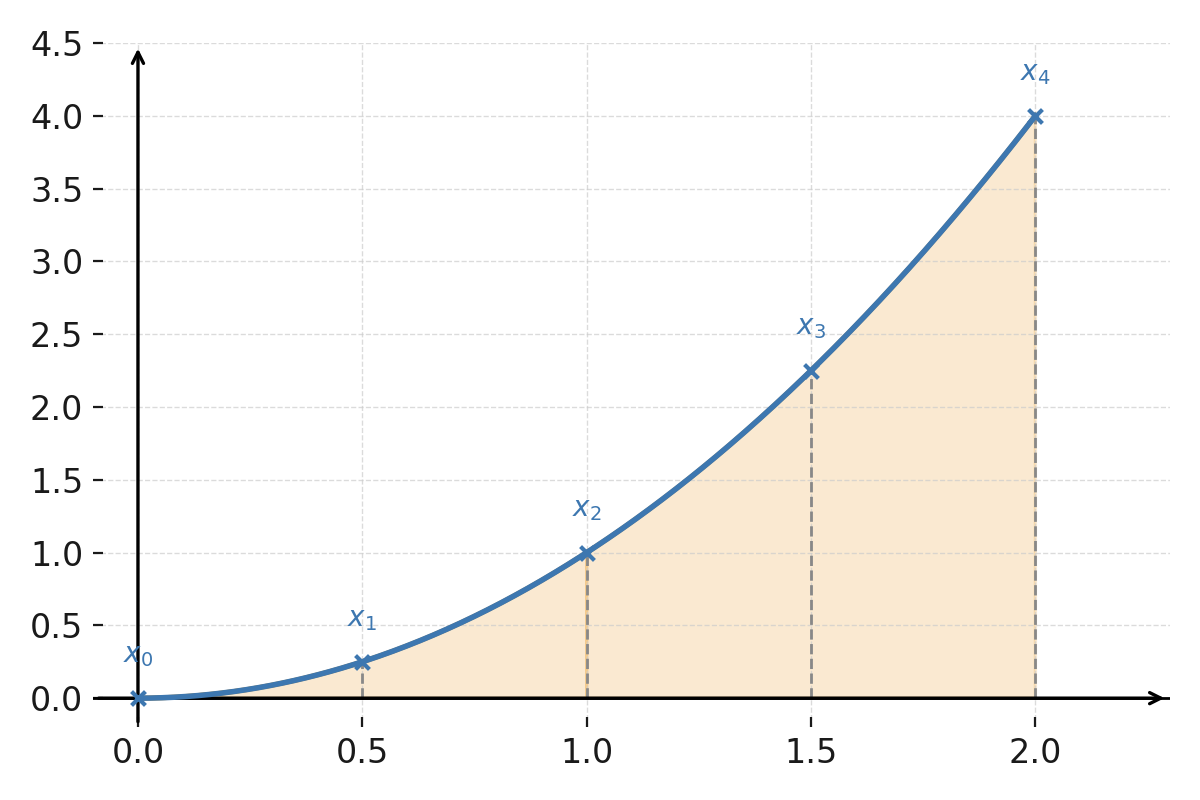
La función \( \large f(x)=x^2 \).
Sobre cada par de subintervalos se traza una parábola que aproxima la función. Los límites \( \large x_0, x_1, x_2, x_3, x_4 \) están marcados con líneas grises discontinuas.
Observaciones
La regla de Simpson ofrece una precisión mucho mayor que el método del trapecio, ya que tiene en cuenta la curvatura de la función. Sin embargo, solo puede aplicarse cuando el número de subintervalos \( \large n \) es par. Cuando se combina con varias parábolas, el método se denomina regla compuesta de Simpson.