Método de la secante
El método de la secante es una técnica numérica para encontrar una raíz de una función, es decir, un punto donde \( \large f(x) = 0 \). Se asemeja al método de Newton-Raphson, pero en lugar de usar la derivada \( \large f'(x) \), la tangente se reemplaza por una secante trazada a través de dos puntos de la gráfica.
Idea del método
En cada paso, se utilizan los dos puntos más recientes \( \large (x_{n-1}, f(x_{n-1})) \) y \( \large (x_n, f(x_n)) \) para formar una línea recta (secante). El punto donde la secante corta el eje x se usa como nueva estimación \( \large x_{n+1} \). El proceso se repite hasta que dos estimaciones consecutivas estén muy cercanas.
Fórmula
$$ \large x_{n+1} = x_n - f(x_n) \cdot \frac{x_n - x_{n-1}}{f(x_n) - f(x_{n-1})} $$
Procedimiento paso a paso
- Elegir dos valores iniciales \( \large x_0 \) y \( \large x_1 \), donde la función tenga signos opuestos.
- Calcular \( \large f(x_0) \) y \( \large f(x_1) \).
- Usar la fórmula para encontrar \( \large x_2 \).
- Repetir el cálculo de manera que \( \large x_{n+1} \) se obtenga a partir de los dos puntos más recientes \( \large x_n \) y \( \large x_{n-1} \).
- Detener cuando \( \large |x_{n+1} - x_n| < \varepsilon \).
Ejemplo
Buscamos la raíz de \( \large f(x) = x^3 - x - 2 \).
Elegimos \( \large x_0 = 1 \) y \( \large x_1 = 2 \).
$$ \large f(1) = -2, \quad f(2) = 4 $$
$$ \large x_2 = 2 - 4 \cdot \frac{2 - 1}{4 - (-2)} $$
$$ \large x_2 = 2 - 4 \cdot \frac{1}{6} $$
$$ \large x_2 = 1{,}333 $$
El nuevo punto \( \large x_2 = 1{,}333 \) se usa junto con \( \large x_1 = 2 \) para calcular el siguiente valor:
$$ \large x_3 = 1{,}333 - f(1{,}333) \cdot \frac{1{,}333 - 2}{f(1{,}333) - f(2)} $$
Después de algunas iteraciones, se obtiene una raíz \( \large x \approx 1{,}521 \), el mismo resultado que con Newton-Raphson, pero sin conocer la derivada de la función.
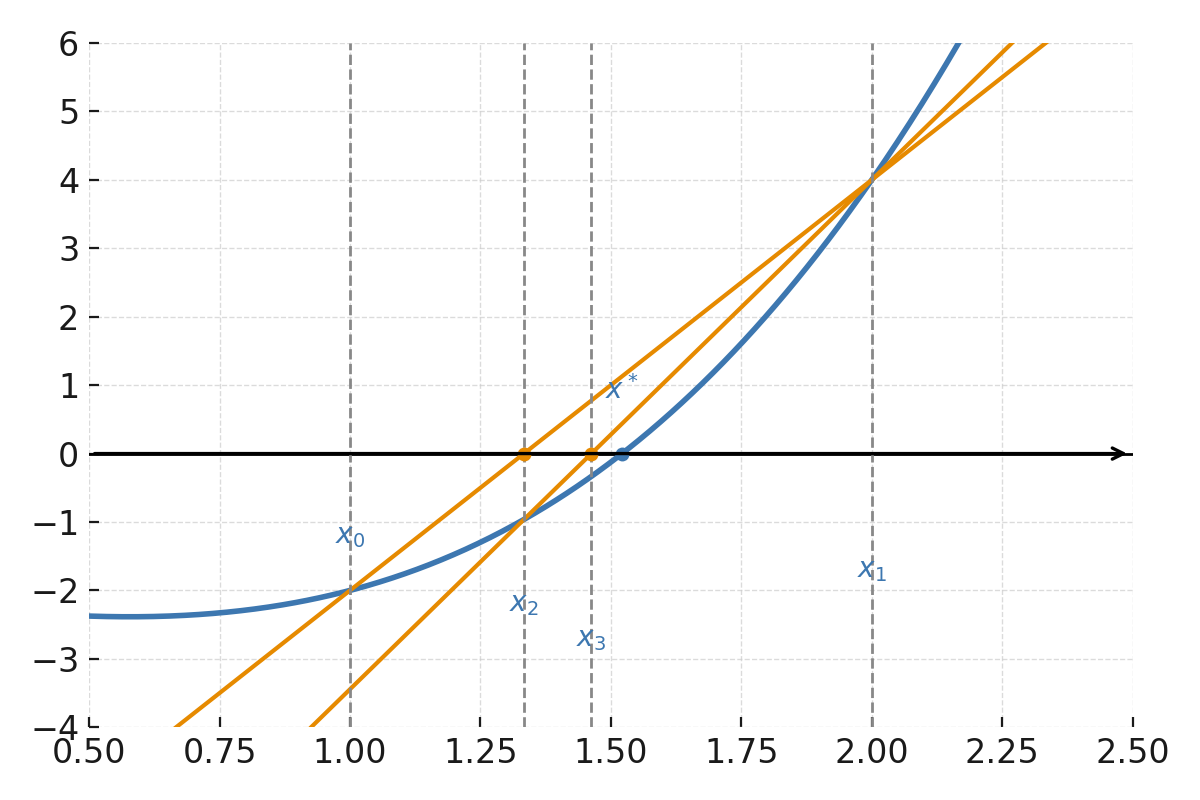
La función \( \large f(x) = x^3 - x - 2 \).
Los puntos \( \large (x_0, f(x_0)) \) y \( \large (x_1, f(x_1)) \) se conectan con una secante que corta el eje x en \( \large x_2 \). Luego se traza una nueva secante entre \( \large (x_1, f(x_1)) \) y \( \large (x_2, f(x_2)) \), que corta el eje aún más cerca de la raíz.
Observaciones
El método de la secante converge más rápido que el método de bisección, pero más lento que Newton-Raphson. Sin embargo, suele ser un buen compromiso, ya que no requiere calcular la derivada de la función.