Ecuaciones diferenciales numéricas (Euler, Runge-Kutta)

Cuando una ecuación diferencial no puede resolverse de forma analítica, es posible encontrar una solución aproximada mediante métodos numéricos. Estos métodos calculan los valores de la función punto por punto a partir de la ecuación diferencial y una condición inicial. Dos de los métodos más utilizados son el método de Euler y el método de Runge–Kutta.

 

 

Idea de las ecuaciones diferenciales numéricas

Una ecuación diferencial ordinaria simple tiene la forma:

 

$$ \large y' = f(x,y) $$

 

Si se conoce un valor inicial \( \large y(x_0) = y_0 \), puede usarse \( \large f(x,y) \) para calcular cómo cambia \( y \) cuando \( x \) aumenta ligeramente. Este proceso se repite paso a paso, construyendo gradualmente una solución numérica.

 

 

Método de Euler

El método de Euler es la solución numérica más sencilla. Utiliza directamente la ecuación diferencial para calcular el siguiente valor como:

 

$$ \large y_{n+1} = y_n + h \cdot f(x_n, y_n) $$

 

Aquí \( \large h \) es el tamaño del paso. Repitiendo con muchos pasos pequeños, se obtiene una curva aproximada de \( y(x) \).

 

 

Ejemplo del método de Euler

Queremos resolver \( \large y' = y \) con la condición inicial \( \large y(0) = 1 \) y \( \large h = 0{,}5 \).

 

Para cada paso:

 

$$ \large y_{n+1} = y_n + 0{,}5 \cdot y_n = 1{,}5y_n $$

 

Después de cuatro pasos obtenemos:

 

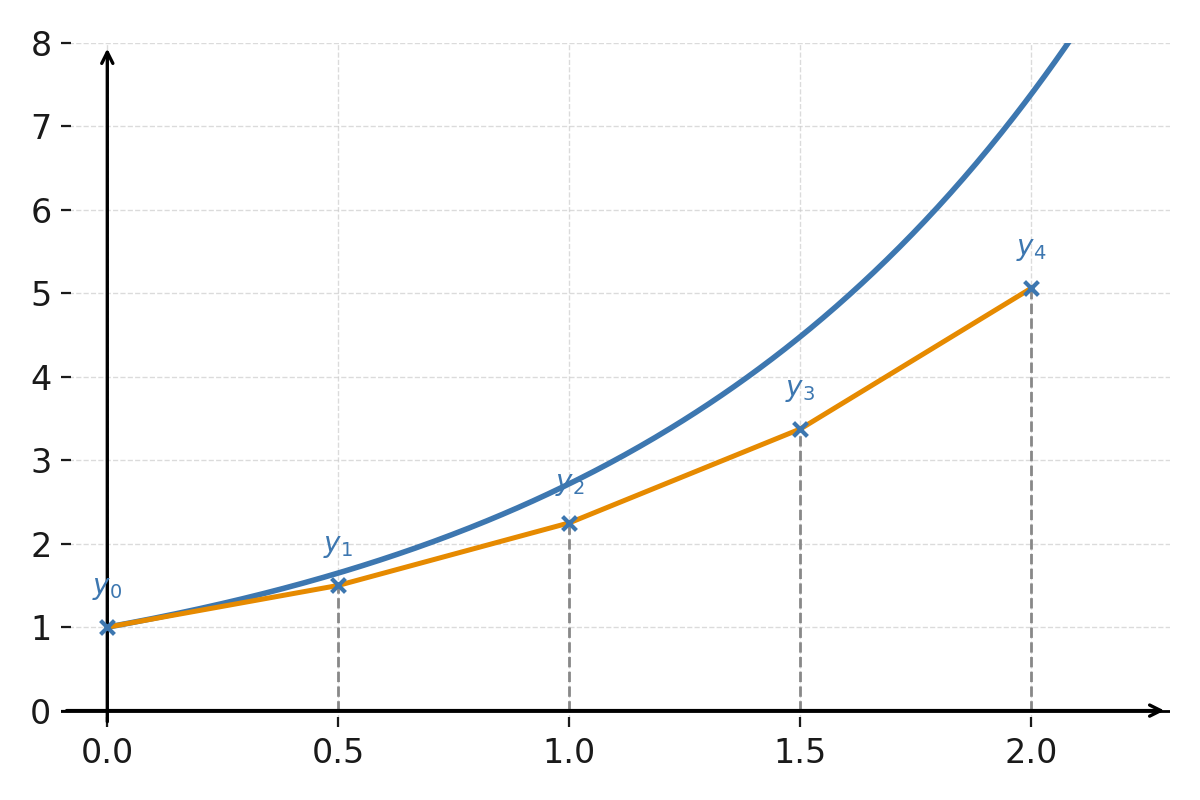
$$ \large y_1 = 1{,}5, \quad y_2 = 2{,}25, \quad y_3 = 3{,}375, \quad y_4 = 5{,}0625 $$

 

La solución exacta es \( \large y = e^x \), y para \( \large x=2 \) se obtiene \( \large e^2 \approx 7{,}389 \). El método de Euler subestima la curva real porque cada paso usa una línea recta en lugar de la función curva.

 

 

 

 

Método de Runge–Kutta (4.ª orden)

Para una mayor precisión se puede usar el método de Runge–Kutta de cuarto orden (RK4). Este toma el promedio de cuatro pendientes en lugar de solo una:

 

$$
\large
\begin{aligned}
k_1 &= f(x_n, y_n) \\[8pt]
k_2 &= f\!\left(x_n + \frac{h}{2},\, y_n + \frac{h}{2}k_1\right) \\[8pt]
k_3 &= f\!\left(x_n + \frac{h}{2},\, y_n + \frac{h}{2}k_2\right) \\[8pt]
k_4 &= f\!\left(x_n + h,\, y_n + h k_3\right) \\[8pt]
y_{n+1} &= y_n + \frac{h}{6}\!\left(k_1 + 2k_2 + 2k_3 + k_4\right)
\end{aligned}
$$

 

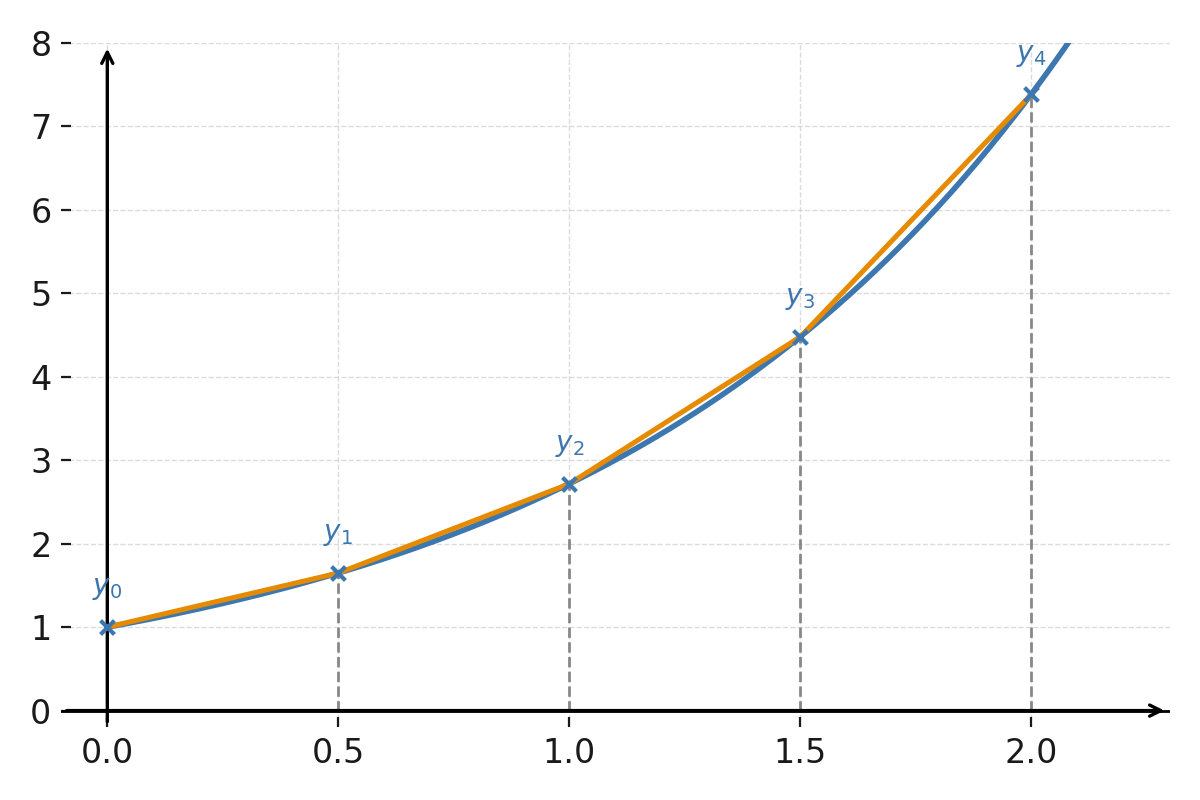
RK4 es mucho más preciso que el método de Euler, incluso con pocos pasos, y por eso se usa con frecuencia en la práctica.

 

 

 

 

Observaciones

Las ecuaciones diferenciales numéricas son una de las herramientas más importantes en matemáticas aplicadas, física e ingeniería. Se utilizan para simular sistemas en los que se conoce la tasa de cambio pero no existe una fórmula cerrada para la función.