Diferenciación numérica
Cuando no se dispone de una fórmula analítica para la función, la derivada \( \large f'(x) \) puede encontrarse mediante métodos numéricos. La diferenciación numérica se basa en aproximar la pendiente de la tangente a partir de puntos discretos en lugar de usar el valor límite exacto.
Idea del método
La derivada en un punto describe la pendiente local de la tangente de la función. Si se conocen los valores de la función en puntos cercanos entre sí, se puede calcular una pendiente aproximada entre ellos. Esto se hace utilizando cocientes de diferencias.
Diferencia hacia adelante, hacia atrás y central
Existen tres fórmulas básicas para la diferenciación numérica:
Diferencia hacia adelante:
$$ \large f'(x) \approx \frac{f(x+h) - f(x)}{h} $$
Diferencia hacia atrás:
$$ \large f'(x) \approx \frac{f(x) - f(x-h)}{h} $$
Diferencia central:
$$ \large f'(x) \approx \frac{f(x+h) - f(x-h)}{2h} $$
La diferencia central suele ofrecer la mejor precisión, porque tiene en cuenta los puntos a ambos lados de \( \large x \).
Ejemplo
Supongamos que queremos calcular la derivada de \( \large f(x) = x^2 \) en el punto \( \large x = 1 \) con \( \large h = 0{,}1 \).
Los valores necesarios de la función son:
$$ \large f(1+h) = f(1{,}1) = 1{,}21, \quad f(1-h) = f(0{,}9) = 0{,}81 $$
Sustituyendo en las fórmulas:
$$ \large f'_{\text{adelante}}(1) = \frac{1{,}21 - 1}{0{,}1} = 2{,}1 $$
$$ \large f'_{\text{atrás}}(1) = \frac{1 - 0{,}81}{0{,}1} = 1{,}9 $$
$$ \large f'_{\text{central}}(1) = \frac{1{,}21 - 0{,}81}{0{,}2} = 2{,}0 $$
El valor real de \( \large f'(x) = 2x \) es \( \large 2 \), por lo que la diferencia central proporciona el resultado más preciso.
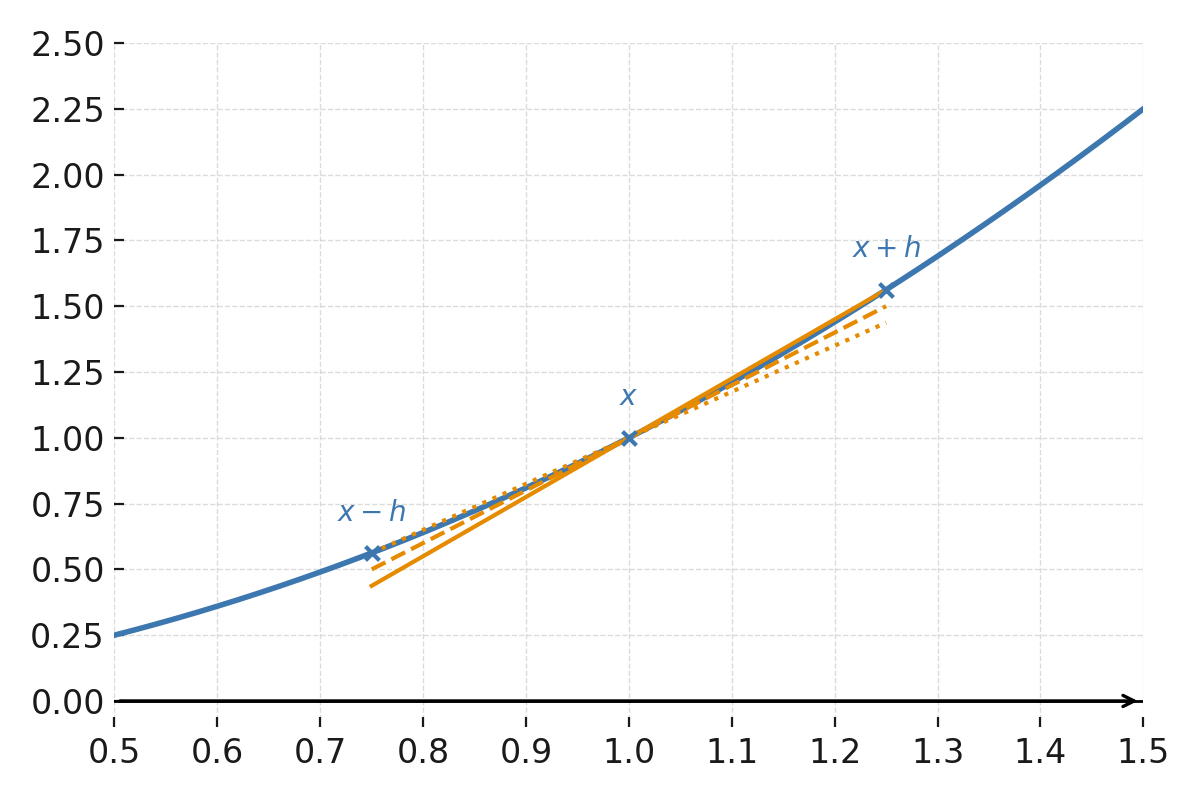
La función \( \large f(x) = x^2 \) alrededor del punto \( \large x=1 \).
Las tres pendientes (adelante, atrás y central) muestran la diferencia entre usar los puntos \( \large (x,f(x)) \), \( \large (x+h,f(x+h)) \) y \( \large (x-h,f(x-h)) \).
Observaciones
La precisión depende de cuán pequeño sea \( \large h \). Un \( \large h \) demasiado grande da una mala aproximación, mientras que uno demasiado pequeño puede causar errores de redondeo. En la práctica, se elige \( \large h \) de modo que el cociente de diferencias sea estable y proporcione una precisión razonable.