Statistische Wahrscheinlichkeit

Wahrscheinlichkeit kann auf zwei Arten berechnet werden: theoretisch (klassisch) und statistisch (empirisch).

 

Klassische Wahrscheinlichkeit

Wenn man den Ergebnisraum kennt und alle Ergebnisse gleich wahrscheinlich sind, kann man die Formel verwenden:

 

$$ \large P(A) = \frac{\text{Anzahl günstiger Ergebnisse}}{\text{Anzahl möglicher Ergebnisse}} $$

 

Beispiel: Die Wahrscheinlichkeit, mit einem Würfel eine Sechs zu werfen, beträgt:

 

$$ \large \frac{1}{6} \approx 0.167 = 16.7\% $$

 

 

Statistische (empirische) Wahrscheinlichkeit

Manchmal kann die Wahrscheinlichkeit nicht direkt berechnet werden. Stattdessen führt man Versuche oder Experimente durch und verwendet die Beobachtungen zur Berechnung der Wahrscheinlichkeit.

 

Beispiel: Wir würfeln 1.000 Mal und notieren Häufigkeit und relative Häufigkeit:

 

	1	2	3	4	5	6
$$ h(x) $$	$$ 180 $$	$$ 176 $$	$$ 149 $$	$$ 170 $$	$$ 167 $$	$$ 158 $$
$$ f(x) $$	$$ \tfrac{180}{1000} $$	$$ \tfrac{176}{1000} $$	$$ \tfrac{149}{1000} $$	$$ \tfrac{170}{1000} $$	$$ \tfrac{167}{1000} $$	$$ \tfrac{158}{1000} $$
Erwartet	$$ \tfrac{1000}{6} \approx 167 $$	$$ 167 $$	$$ 167 $$	$$ 167 $$	$$ 167 $$	$$ 167 $$

 

 

Diagramm

Das folgende Balkendiagramm zeigt die theoretische Wahrscheinlichkeit (167 für jede Seite) im Vergleich zu den empirischen Ergebnissen.

 

 

 

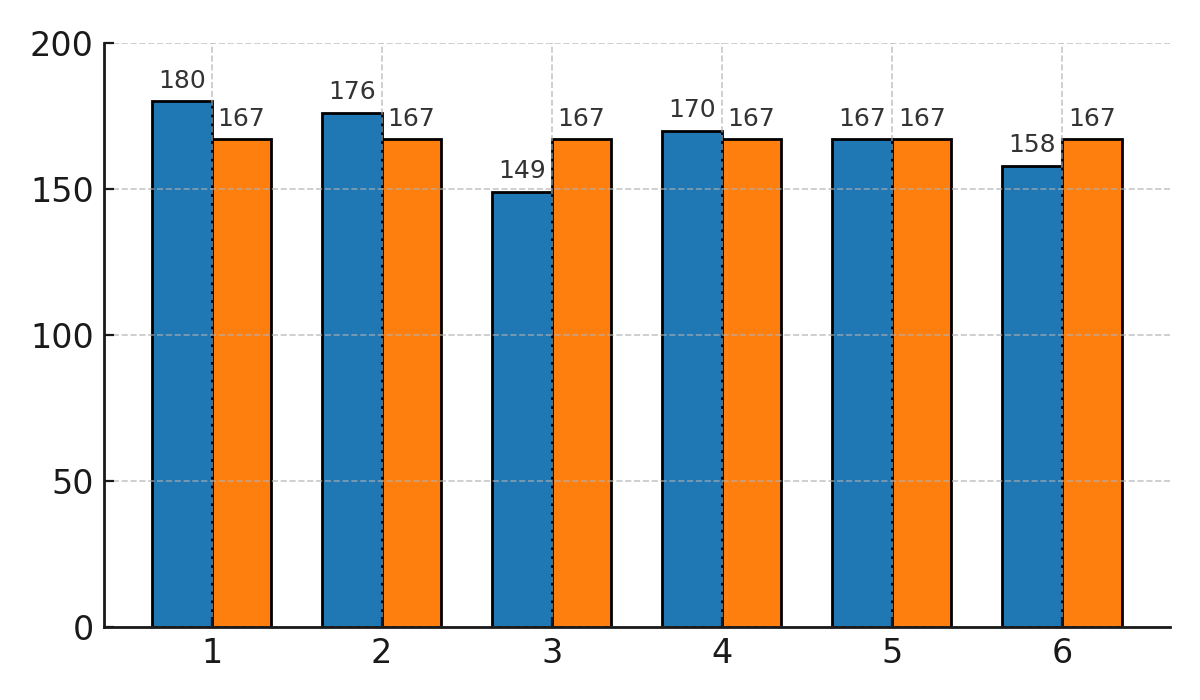
Vergleich

Wir wissen, dass die Wahrscheinlichkeit, eine Sechs zu würfeln, beträgt:

 

$$ \large \tfrac{1}{6} \approx 0.167 = 16.7\% $$

 

Unser Experiment zeigte stattdessen:

 

$$ \large \tfrac{158}{1000} = 0.158 = 15.8\% $$

 

Das Ergebnis ist nicht genau dasselbe wie der theoretische Wert, liegt aber nahe. Dies zeigt, wie die statistische Wahrscheinlichkeit verwendet wird, um die theoretische Wahrscheinlichkeit durch Beobachtungen anzunähern.

 

Die statistische Wahrscheinlichkeit ist daher ein praktisches Werkzeug, wenn man die Wahrscheinlichkeit nicht direkt berechnen kann, sondern sich auf Beobachtungen stützen muss.