Gesetz der großen Zahlen

Das Gesetz der großen Zahlen ist ein grundlegendes Prinzip der Wahrscheinlichkeitsrechnung.

Es besagt, dass je öfter man ein Experiment wiederholt, desto näher liegen die beobachteten Ergebnisse an der theoretischen Wahrscheinlichkeit.

 

 

Beispiel mit einem Würfel

Wenn man einen Würfel einmal wirft, gibt es keine Garantie, eine Sechs zu erhalten.

Wenn man ihn 6 Mal wirft, kann es durchaus vorkommen, dass keine einzige Sechs erscheint.

Wenn man ihn 1.000 Mal wirft, wird man typischerweise feststellen, dass etwa ein Sechstel der Würfe eine Sechs ergibt – also ungefähr 167 Mal.

 

 

Theoretische Wahrscheinlichkeit

Wir wissen, dass die Wahrscheinlichkeit, eine Sechs zu würfeln, ist:

 

$$ P(\text{Sechs}) = \tfrac{1}{6} \approx 0,167 = 16,7\% $$

 

Statistische Wahrscheinlichkeit

In einem Experiment mit 1.000 Würfen erhalten wir vielleicht das Ergebnis:

 

• Anzahl der Sechsen: 158
• Statistische Wahrscheinlichkeit: \( \tfrac{158}{1000} = 0,158 = 15,8\% \)

 

Das liegt nahe am theoretischen Wert von 16,7 %.

 

 

 

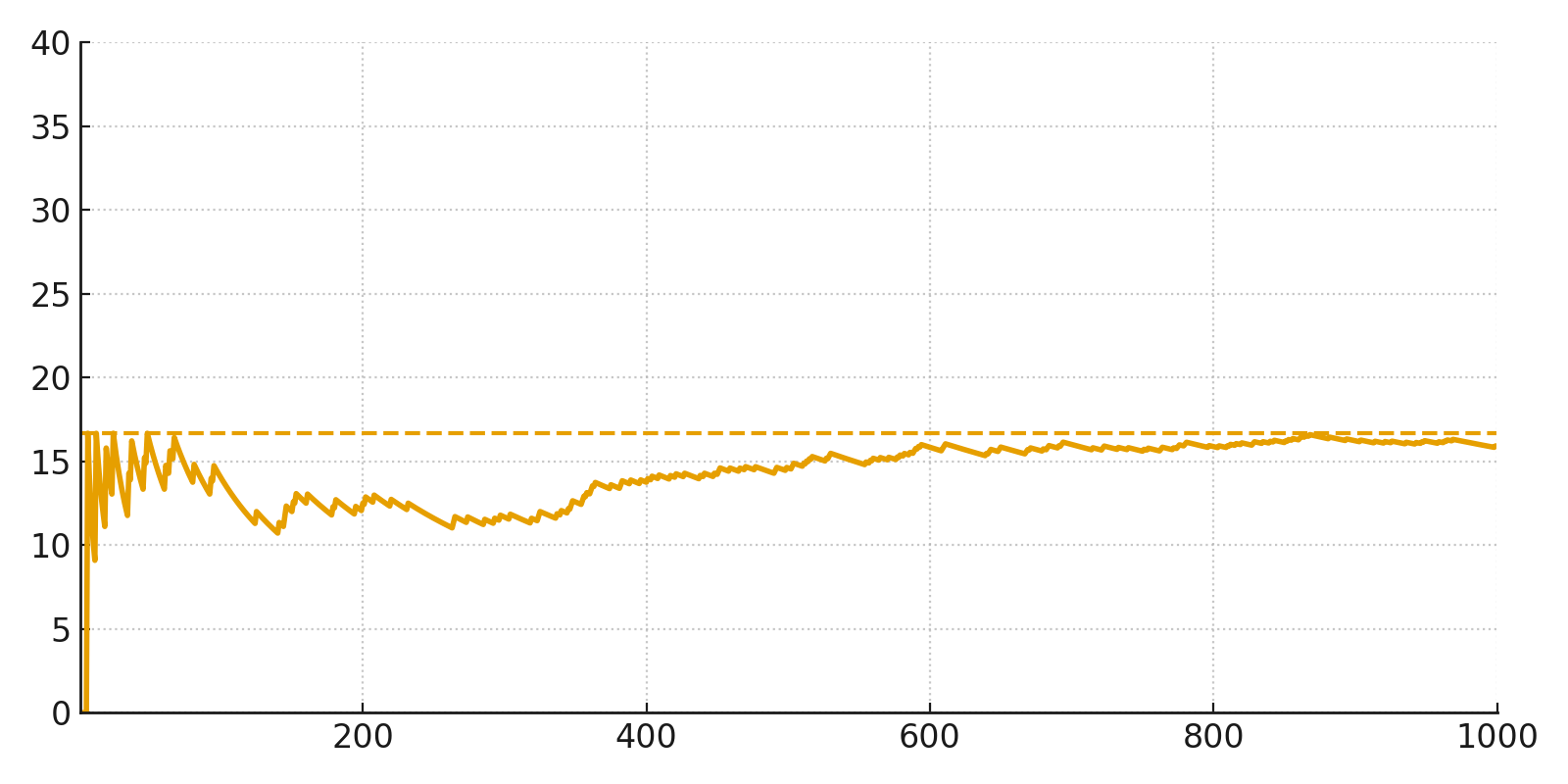
Hier haben wir einen Würfel 1.000 Mal geworfen und den Prozentsatz der Würfe verfolgt, die eine Sechs ergaben.

Am Anfang schwankt die Kurve stark, aber mit zunehmender Anzahl der Würfe stabilisiert sie sich um die theoretische Wahrscheinlichkeit von etwa 16,7 %.

Genau das bedeutet das Gesetz der großen Zahlen: Wahrscheinlichkeiten ergeben erst dann Sinn, wenn man viele Beobachtungen hat.

 

 

Bedeutung

Das Gesetz der großen Zahlen zeigt, warum Wahrscheinlichkeiten in der Praxis sinnvoll sind:

 

• Kleine Datensätze können zufällige Schwankungen ergeben.
• Große Datensätze liefern ein zuverlässigeres Bild.

 

 

Zusammenfassung

• Das Gesetz der großen Zahlen gilt für viele Wiederholungen eines Experiments.
• Die empirischen Häufigkeiten nähern sich den theoretischen Wahrscheinlichkeiten an.
• Je größer die Stichprobe, desto genauer das Ergebnis.