Linearisierung und Näherung
Die Differentialrechnung ermöglicht es, Funktionen lokal zu verstehen und zu approximieren. Wenn eine Funktion glatt und differenzierbar ist, kann sie in einem kleinen Bereich um einen Punkt durch eine gerade Linie ersetzt werden – nämlich durch die Tangente. Diese Methode heißt Linearisierung und wird verwendet, um schnelle Näherungen zu finden, wenn genaue Berechnungen schwierig oder unnötig sind.
Die Idee der Linearisierung
In der Nähe eines Punktes \( \large x_0 \) verhält sich eine differenzierbare Funktion \( \large f(x) \) fast wie ihre Tangente. Wenn man die Funktion und ihre Ableitung an diesem Punkt kennt, kann man ihr gesamtes lokales Verhalten durch eine lineare Funktion beschreiben, mit der sich leicht rechnen lässt.
Die lineare Näherung (die Tangentengleichung) hat die Form:
$$ \large f(x) \approx f(x_0) + f'(x_0) \cdot (x - x_0) $$
Dieser Ausdruck besagt, dass der Funktionswert an einem Punkt nahe \( \large x_0 \) durch den Wert in \( \large x_0 \) plus die durch die Steigung \( \large f'(x_0) \) gegebene Änderung angenähert werden kann. Je näher \( \large x \) bei \( \large x_0 \) liegt, desto besser funktioniert die Näherung.
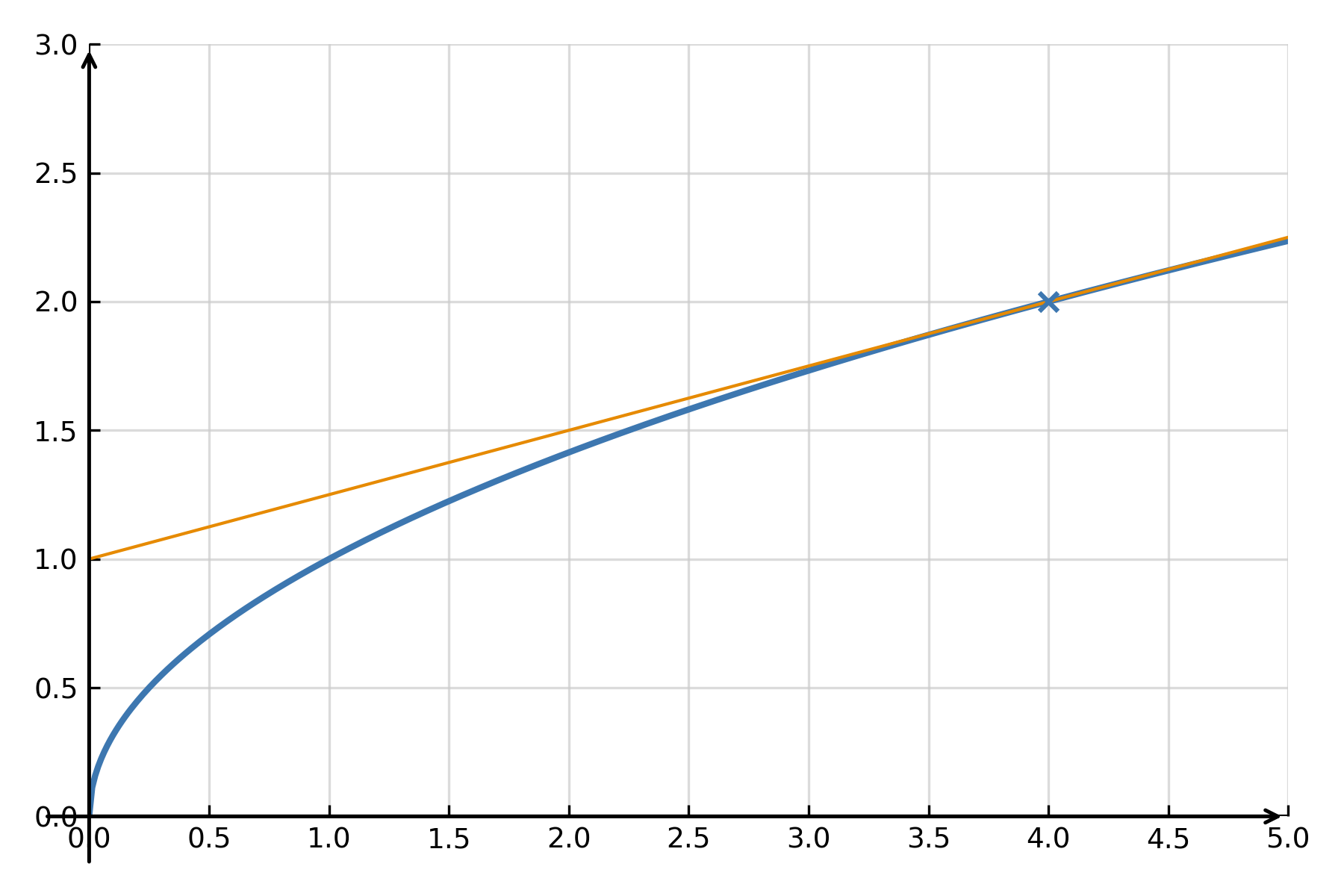
Grafisches Verständnis
Die Tangente „berührt“ den Graphen von \( \large f(x) \) in genau einem Punkt und folgt dort ihrer Richtung. Bei kleinen Änderungen von \( \large x \) liegen Funktion und Tangente fast übereinander. Linearisierung bedeutet also, eine gekrümmte Kurve durch ihre lokale Gerade zu ersetzen. Dadurch werden Berechnungen deutlich einfacher, ohne an Genauigkeit in diesem Bereich zu verlieren.
Beispiel 1: Linearisierung einer quadratischen Funktion
Finde die lineare Näherung von \( \large f(x) = x^2 \) um den Punkt \( \large x_0 = 2 \).
Es gilt \( \large f(2) = 4 \) und \( \large f'(x) = 2x \), also \( \large f'(2) = 4 \). Damit gilt:
$$ \large f(x) \approx 4 + 4(x - 2) = 4x - 4 $$
Wenn \( \large x \) nahe bei 2 liegt, ist \( \large 4x - 4 \) eine gute Näherung für \( \large x^2 \). Zum Beispiel ergibt \( \large f(2.1) \approx 4.4 \), während der exakte Wert \( \large 2.1^2 = 4.41 \) ist.
Beispiel 2: Näherung einer Quadratwurzel
Die Linearisierung kann verwendet werden, um Quadratwurzeln ohne Taschenrechner zu nähern. Zum Beispiel kann \( \large \sqrt{4.1} \) gefunden werden, indem man die Funktion \( \large f(x) = \sqrt{x} \) um \( \large x_0 = 4 \) linearisiert.
Hier gilt \( \large f(4) = 2 \) und \( \large f'(x) = \frac{1}{2\sqrt{x}} \), also \( \large f'(4) = \frac{1}{4} \).
$$ \large f(x) \approx 2 + \frac{1}{4}(x - 4) $$
Für \( \large x = 4.1 \): \( \large f(4.1) \approx 2 + \frac{1}{4} \cdot 0.1 = 2.025 \), während der genaue Wert \( \large 2.0248 \) ist. Die Tangentennäherung liefert also ein Ergebnis mit nahezu keinem Fehler.
Fehler und Genauigkeit
Je näher \( \large x \) bei \( \large x_0 \) liegt, desto besser funktioniert die Näherung. Entfernt man sich weiter, beginnt die Tangente von der ursprünglichen Kurve abzuweichen, da höhergradige Änderungen (Krümmung) eine Rolle spielen. Dies kann korrigiert werden, indem man weitere Glieder in eine Taylor-Entwicklung einbezieht.
In erster Ordnung entspricht die Linearisierung dem ersten Teil der Taylorreihe:
$$ \large f(x) = f(x_0) + f'(x_0)(x - x_0) + \frac{f''(x_0)}{2!}(x - x_0)^2 + \dots $$
Nimmt man nur das erste Glied nach \( \large f(x_0) \), erhält man genau die Tangentennäherung. Daher wird die Methode auch Taylor-Näherung erster Ordnung genannt.
Beispiel 3: Physikalische Interpretation
In der Physik wird die Linearisierung verwendet, um Bewegungen oder Prozesse in kurzen Zeitintervallen zu beschreiben. Wenn \( \large s(t) \) eine Position beschreibt, gilt für die lineare Näherung:
$$ \large s(t) \approx s(t_0) + v(t_0) \cdot (t - t_0) $$
Das kann so interpretiert werden: „die neue Position ist die alte plus Geschwindigkeit mal Zeit“. Hier spielt die Geschwindigkeit \( \large v(t_0) = s'(t_0) \) genau dieselbe Rolle wie die Steigung der Tangente in der Mathematik.
Zusammenfassung
Die Linearisierung ermöglicht es, eine Funktion durch ein einfaches lineares Modell um einen gegebenen Punkt zu ersetzen. Die Tangente dient als lokale Näherung, die schnell berechnet werden kann und oft ausreichend genau ist. Die Methode bildet die Grundlage vieler numerischer Verfahren und der Taylor-Entwicklung, die die Idee auf genauere Näherungen erweitert.