Die Ableitungsfunktion

Die Ableitungsfunktion zeigt, wie schnell sich eine andere Funktion ändert. Wenn \( \large f(x) \) eine Größe beschreibt, gibt die Ableitung \( \large f'(x) \) an, wie stark sich diese Größe verändert, wenn \( \large x \) sich geringfügig ändert. Auf diese Weise wird die Differentialrechnung zu einem präzisen Werkzeug zur Messung von Veränderungen.

 

 

Von der Sekante zur Tangente

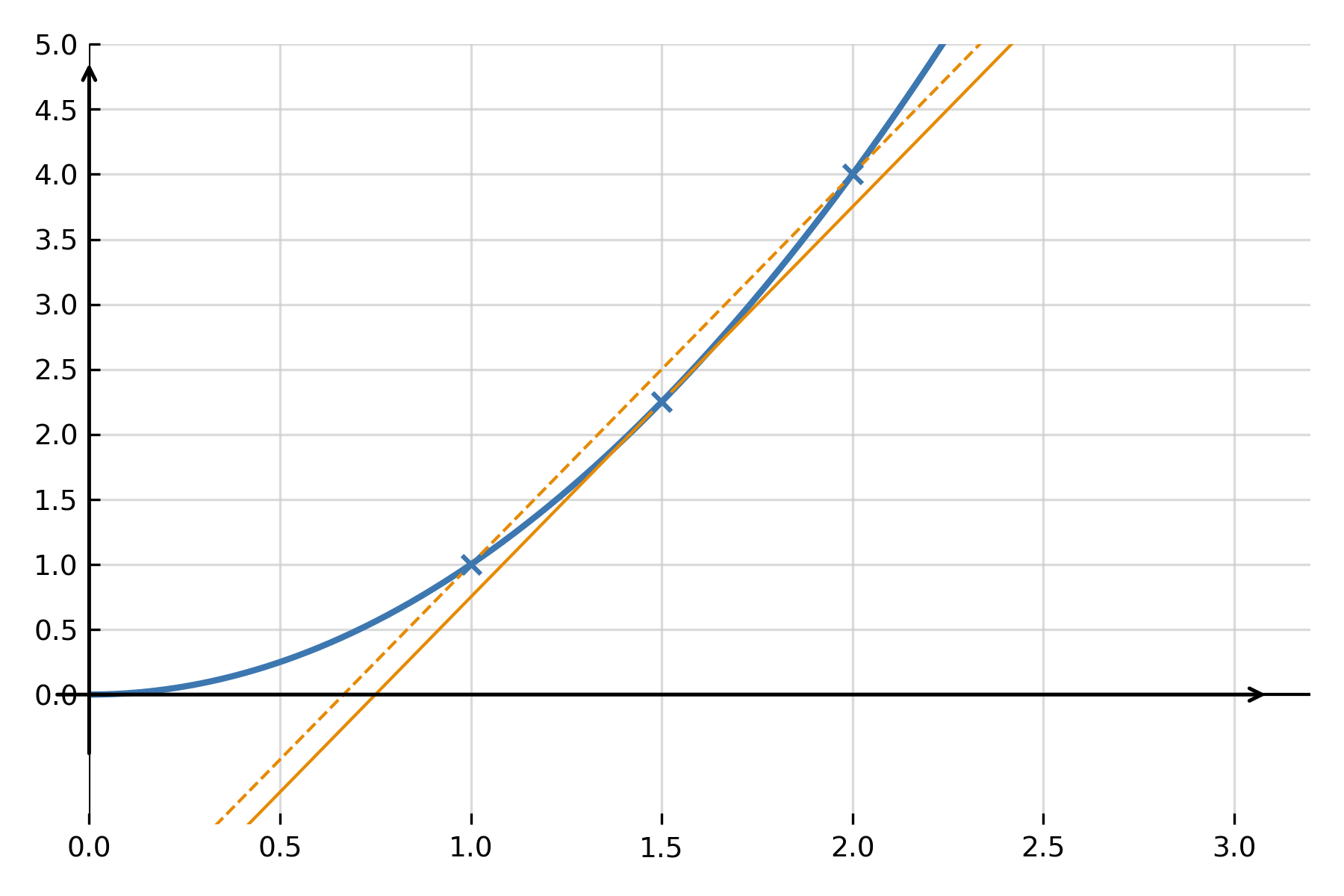
Um zu verstehen, was „differenzieren“ bedeutet, beginnt man mit der Steigung einer Sekante. Eine Sekante ist die Gerade, die zwei Punkte auf dem Graphen von \( \large f(x) \) verbindet. Die Steigung der Sekante zeigt, wie stark die Funktion im Durchschnitt zwischen den beiden Punkten steigt oder fällt.

 

$$ \large a_{\text{Sekante}} = \frac{f(x+h) - f(x)}{h} $$

 

Wenn man die Punkte immer näher wählt, sodass \( \large h \) sehr klein wird, nähert sich die Sekante einer Geraden, die den Graphen nur in einem Punkt berührt — der Tangente. Die Steigung dieser Tangente nennt man die momentane Änderungsrate. Dies ist genau der Wert, den die Ableitungsfunktion liefert.

 

 

 

 

Definition über den Grenzwert

Die genaue Definition der Ableitungsfunktion lautet:

 

$$ \large f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} $$

 

Der Bruch misst, wie stark sich \( \large f(x) \) ändert, wenn \( \large x \) um eine kleine Zahl \( \large h \) verändert wird. Wenn \( \large h \) gegen null geht, erhält man die Änderung genau an diesem Punkt — die Steigung der Tangente. Der Grenzwert existiert nur, wenn die Funktion an diesem Punkt hinreichend glatt ist, also keine Sprünge, Spitzen oder Knicke aufweist.

 

 

Notation und Bedeutung

Es gibt mehrere Möglichkeiten, die Ableitung zu schreiben:

 

$$ \large f'(x) \quad \text{oder} \quad \frac{dy}{dx} \quad \text{oder} \quad Df(x) $$

 

Alle drei bedeuten dasselbe: wie stark sich \( \large y \) ändert, wenn \( \large x \) sich ändert. In der Physik liest man zum Beispiel \( \large \frac{dy}{dt} \) als „Änderung des Weges über die Änderung der Zeit“, also Geschwindigkeit.

 

 

Grafisches Verständnis

Die Ableitungsfunktion ergibt eine neue Funktion, die an jedem Punkt die Steigung des Graphen von \( \large f(x) \) angibt. Wo der Graph steigt, ist die Ableitung positiv; wo er fällt, ist sie negativ; und wo der Graph eine waagrechte Tangente hat, ist die Ableitung null.

 

Ein Punkt, an dem \( \large f'(x) = 0 \) gilt, wird als stationärer Punkt bezeichnet. Solche Punkte spielen später eine wichtige Rolle, wenn man Maxima und Minima einer Funktion bestimmen will.

 

 

Physikalische Bedeutung

In vielen Zusammenhängen stellt die Ableitung eine physikalische Größe dar. Wenn \( \large f(x) \) die Position als Funktion der Zeit beschreibt, dann ist \( \large f'(x) \) die Geschwindigkeit — also, wie schnell sich die Position ändert. Wenn man noch einmal differenziert, erhält man die Beschleunigung \( \large f''(x) \), die zeigt, wie schnell sich die Geschwindigkeit selbst verändert.

 

 

Beispiele

1. Beispiel – quadratische Funktion

Für \( \large f(x) = x^2 \) kann die Ableitung direkt aus der Definition berechnet werden:

 

$$ \large f'(x) = \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} = \lim_{h \to 0} \frac{2xh + h^2}{h} = 2x $$

 

Die Ableitungsfunktion ist \( \large f'(x) = 2x \). Die Steigung hängt also davon ab, wo man sich auf dem Graphen befindet. Im Punkt \( \large x = 3 \) ist die Steigung \( \large f'(3) = 6 \).

 

2. Beispiel – lineare Funktion

Für \( \large f(x) = 5x + 2 \) ist der Graph bereits eine Gerade. Ihre Steigung ist konstant, daher gilt:

 

$$ \large f'(x) = 5 $$

 

Hier steigt die Funktion immer um 5 Einheiten, wenn \( \large x \) um 1 zunimmt. Das zeigt, dass die Differentialrechnung den bekannten Steigungsbegriff von Geraden auf alle glatten Funktionen verallgemeinert.

 

3. Beispiel – physikalische Interpretation

Wenn \( \large s(t) = t^2 \) den zurückgelegten Weg eines Autos in Metern als Funktion der Zeit \( \large t \) in Sekunden beschreibt, dann ist die Geschwindigkeit \( \large v(t) = s'(t) = 2t \). Nach 4 Sekunden fährt das Auto also mit \( \large v(4) = 8 \) m/s. Die Ableitung liefert hier ein direktes Maß für die Bewegungsgeschwindigkeit.

 

 

Kurzregeln

Beim Finden der Ableitungen gebräuchlicher Funktionen gelten einige einfache Regeln:

 

$$ \large (k)' = 0 \qquad (x^n)' = n \cdot x^{n-1} \qquad (k \cdot f(x))' = k \cdot f'(x) $$

 

Diese bilden die Grundlage der allgemeinen Ableitungsregeln, die im nächsten Abschnitt behandelt werden. Mit ihnen lassen sich auch ziemlich komplexe Funktionen differenzieren, ohne zur Grenzwertdefinition zurückzukehren.

 

 

Zusammenfassung

Die Ableitungsfunktion beschreibt, wie schnell sich eine Funktion an jedem Punkt ändert. Sie kann als Steigung der Tangente, als Maß der Änderungsrate oder als mathematisches Werkzeug zur Beschreibung von Bewegung und Wachstum verstanden werden. Sie spielt eine zentrale Rolle in nahezu allen Bereichen der Mathematik, Physik und Wirtschaft.