Erweiterte Methoden

Wenn man die grundlegenden Rechenregeln der Differentialrechnung beherrscht, öffnet sich eine neue Welt von Möglichkeiten. Viele Funktionen lassen sich nicht direkt als \( \large y = f(x) \) schreiben, können aber dennoch mit erweiterten Methoden differenziert werden. Die drei wichtigsten Techniken sind implizite Differentiation, parametrische Differentiation und die Ableitung inverser Funktionen.

 

 

Implizite Differentiation

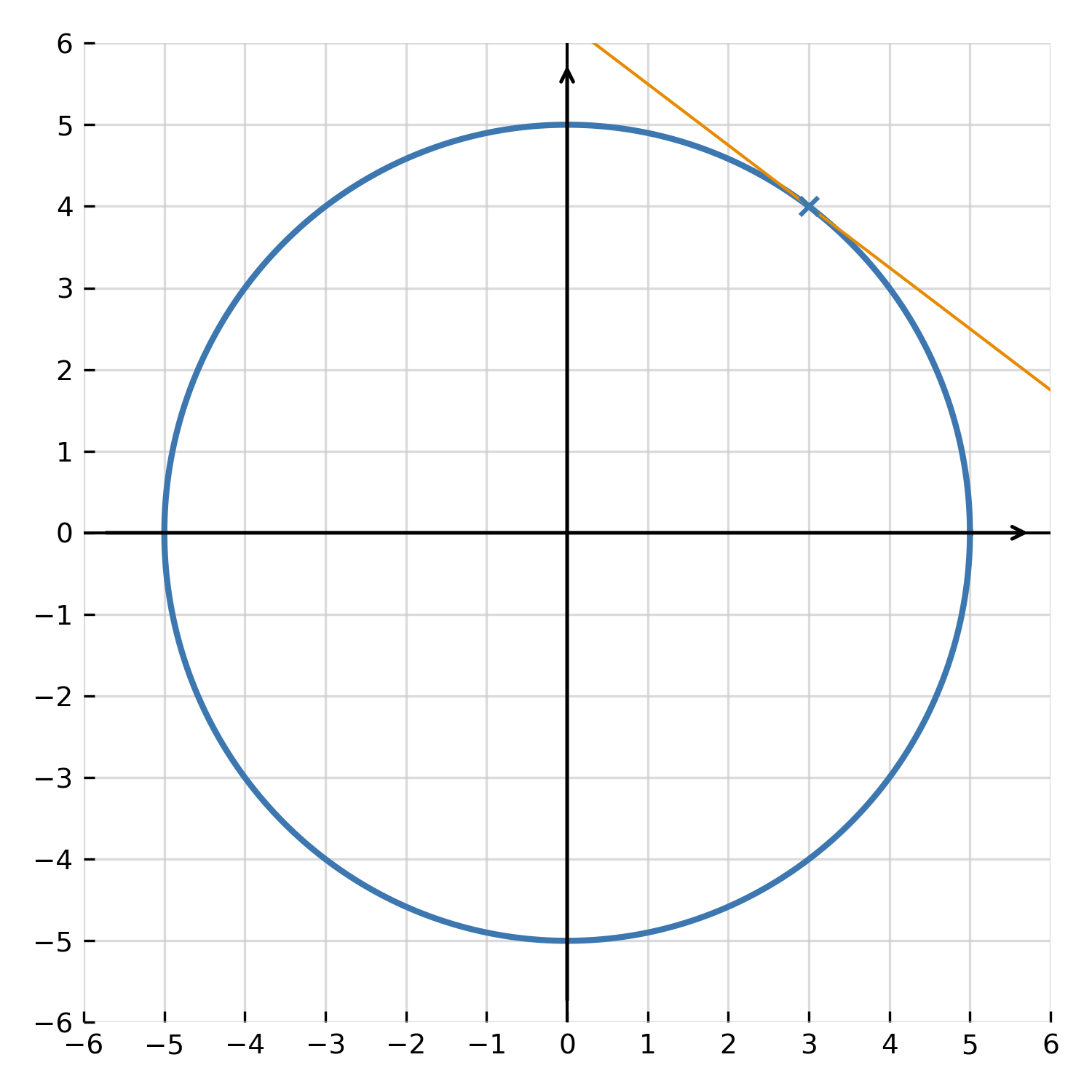
Einige Funktionen sind durch eine Gleichung gegeben, in der \( \large x \) und \( \large y \) gemeinsam auftreten, zum Beispiel \( \large x^2 + y^2 = 25 \). Man kann \( \large y \) nicht direkt isolieren, aber man kann \( \large \frac{dy}{dx} \) finden, indem man beide Seiten nach \( \large x \) ableitet und dabei bedenkt, dass \( \large y \) selbst von \( \large x \) abhängt.

 

Beispiel:

 

Leite \( \large x^2 + y^2 = 25 \) nach \( \large x \) ab:

 

$$ \large 2x + 2y \cdot \frac{dy}{dx} = 0 $$

 

Löse nach \( \large \frac{dy}{dx} \) auf:

 

$$ \large \frac{dy}{dx} = -\frac{x}{y} $$

 

Dies ist die Steigung der Tangente an den Kreis \( \large x^2 + y^2 = 25 \) in jedem Punkt. Implizite Differentiation ist besonders nützlich für Kurven, die nicht als Funktionen im herkömmlichen Sinn beschrieben werden können, wie Kreise, Ellipsen und Hyperbeln.

 

Kettenregel in der Praxis

Die Kettenregel wird verwendet, wenn eine Funktion aus einer anderen Funktion besteht. Sie ist in allen erweiterten Methoden zentral. Man kann sie als „eine Änderung beeinflusst eine andere“ verstehen.

 

Beispiel:

 

Wenn \( \large y = \sin(3x^2) \), besteht die Funktion aus zwei Schichten: \( \large \sin(u) \) mit \( \large u = 3x^2 \). Die Ableitung ergibt sich durch Multiplikation der beiden Änderungsraten:

 

$$ \large \frac{dy}{dx} = \cos(3x^2) \cdot 6x = 6x \cos(3x^2) $$

 

Die Kettenregel kann auch mehrfach hintereinander angewendet werden, zum Beispiel, wenn eine Funktion aus drei oder mehr Schichten besteht. Sie ist daher ein unentbehrliches Werkzeug in allen fortgeschrittenen Berechnungen.

 

 

Parametrische Funktionen

Manchmal werden sowohl \( \large x \) als auch \( \large y \) als Funktionen einer dritten Variablen gegeben, die oft \( \large t \) (der Parameter) genannt wird. Das tritt zum Beispiel in der Bewegungslehre auf, wenn sich ein Teilchen im Raum bewegt und seine Position als Funktion der Zeit bekannt ist.

 

Wenn \( \large x = x(t) \) und \( \large y = y(t) \), kann man \( \large \frac{dy}{dx} \) finden, indem man die beiden Ableitungen nach \( \large t \) kombiniert:

 

$$ \large \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} $$

 

Beispiel:

 

Wenn \( \large x = t^2 \) und \( \large y = 3t + 1 \), dann gilt:

$$ \large \frac{dx}{dt} = 2t \qquad \text{und} \qquad \frac{dy}{dt} = 3 $$

 

Daraus folgt:

$$ \large \frac{dy}{dx} = \frac{3}{2t} $$

 

Dieser Ausdruck zeigt die Steigung der Kurve in dem Punkt, der dem Parameter \( \large t \) entspricht.

 

 

Inverse Funktionen

Wenn eine Funktion eine Umkehrfunktion besitzt, kann man auch deren Ableitung finden, ohne sie explizit zu bestimmen. Sei \( \large y = f(x) \) eine differenzierbare Funktion mit der Inversen \( \large x = f^{-1}(y) \). Dann gilt:

 

$$ \large \frac{dy}{dx} = f'(x) \quad \Rightarrow \quad \frac{dx}{dy} = \frac{1}{f'(x)} $$

 

Mit anderen Worten: Die Ableitung der Umkehrfunktion ist der Kehrwert der Ableitung der ursprünglichen Funktion.

 

Beispiel:

 

Wenn \( \large f(x) = e^x \), dann ist \( \large f^{-1}(x) = \ln(x) \). Da \( \large f'(x) = e^x \), folgt:

 

$$ \large (\ln x)' = \frac{1}{e^x} = \frac{1}{x} $$

 

Dies stimmt mit der bekannten Ableitung des Logarithmus überein und zeigt das Prinzip in der Praxis.

 

 

Kombinierte Methoden

Oft trifft man auf Funktionen, bei denen mehrere dieser Techniken gemeinsam angewendet werden müssen — zum Beispiel eine implizite Gleichung, die einen Parameter enthält, oder eine zusammengesetzte Funktion, die invertiert werden muss. Der erfahrene Rechner lernt, die Regeln natürlich zu kombinieren:

 

$$ \large \frac{dy}{dx} = \frac{dy}{dt} \cdot \frac{dt}{dx} $$

 

Dies ist im Grunde nur eine erweiterte Form der Kettenregel, die es erlaubt, bei Bedarf zwischen Variablen zu wechseln.

 

 

Zusammenfassung

Die erweiterten Methoden ermöglichen es, Funktionen zu differenzieren, die nicht in einfacher Form geschrieben werden können. Implizite Differentiation wird für Beziehungen zwischen \( \large x \) und \( \large y \) verwendet, parametrische Differentiation, wenn beide von einem Parameter abhängen, und die Regel für inverse Funktionen erlaubt es, Ableitungen von Logarithmen und inversen trigonometrischen Funktionen zu finden. Diese Werkzeuge erweitern den Anwendungsbereich der Differentialrechnung und bilden die Grundlage für weiterführende Themen in der Analysis.