Anwendungen der Differentialrechnung

Die Differentialrechnung wird nicht nur verwendet, um Steigungen zu berechnen. Sie bietet auch ein tieferes Verständnis dafür, wie sich Funktionen verhalten. Durch das Studium der Ableitung kann man bestimmen, wo eine Funktion steigt oder fällt, ihre Maxima und Minima finden und ihre graphische Form analysieren. Die Methode wird in Bereichen wie Physik, Ökonomie, Biologie und Technik angewendet.

Monotonie: Wo die Funktion steigt und fällt

Die Ableitungsfunktion $ \large f'(x) $ zeigt, ob $ \large f(x) $ in einem gegebenen Intervall steigt oder fällt:

Wenn $ \large f'(x) > 0 $, ist die Funktion steigend.
Wenn $ \large f'(x) < 0 $, ist die Funktion fallend.
Wenn $ \large f'(x) = 0 $, besitzt die Funktion einen stationären Punkt.

Ein stationärer Punkt ist eine Stelle, an der die Steigung der Tangente null ist. Er kann ein lokales Maximum, ein lokales Minimum oder ein Wendepunkt sein.

Beispiel: Analyse einer Funktion

Untersuche die Funktion $ \large f(x) = x^3 - 3x^2 + 2 $.

Zuerst wird die Ableitung berechnet:

$$ \large f'(x) = 3x^2 - 6x = 3x(x - 2) $$

Die Ableitung ist null für $ \large x = 0 $ und $ \large x = 2 $. Wir untersuchen das Vorzeichen von $ \large f'(x) $ in den Intervallen:

Für $ \large x < 0 $: $ \large f'(x) > 0 $ → steigend
Für $ \large 0 < x < 2 $: $ \large f'(x) < 0 $ → fallend
Für $ \large x > 2 $: $ \large f'(x) > 0 $ → steigend

Damit hat die Funktion ein lokales Maximum bei $ \large x = 0 $ und ein lokales Minimum bei $ \large x = 2 $. Diese Methode wird Vorzeichenschema genannt und dient dazu, zu bestimmen, wo die Funktion wächst oder abnimmt.

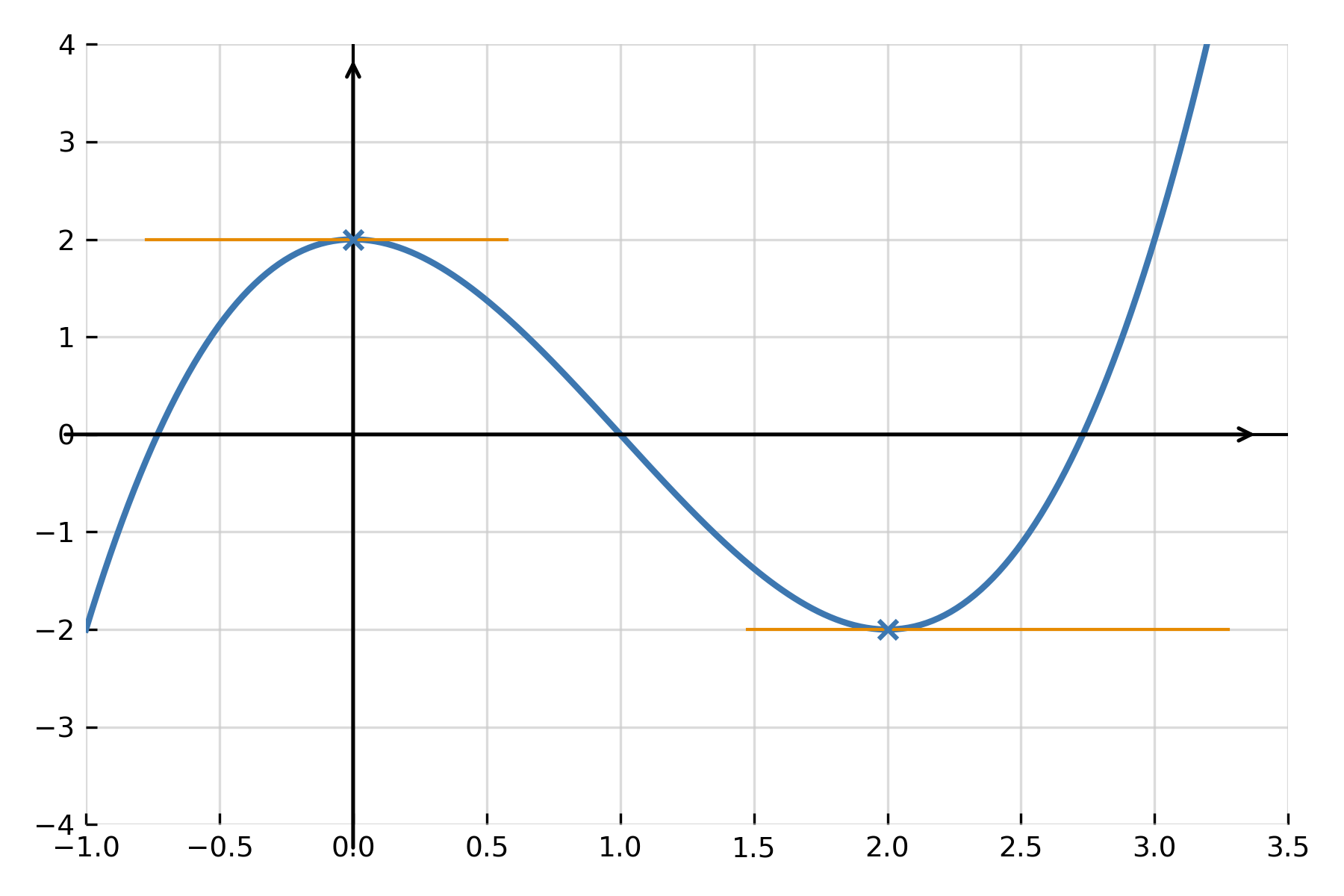
Extremum

Extrema, Maximum und Minimum

Ein Extremum ist ein Punkt, an dem die Funktion von steigend zu fallend (Maximum) oder von fallend zu steigend (Minimum) übergeht. Um die Art zu bestimmen, untersucht man das Vorzeichen von $ \large f'(x) $ um den Punkt herum — oder man verwendet die zweite Ableitung.

Der Test der zweiten Ableitung besagt:

Wenn $ \large f'(x_0) = 0 $ und $ \large f''(x_0) > 0 $, hat die Funktion ein lokales Minimum bei $ \large x_0 $.
Wenn $ \large f'(x_0) = 0 $ und $ \large f''(x_0) < 0 $, hat die Funktion ein lokales Maximum bei $ \large x_0 $.

Beispiel: Für $ \large f(x) = x^3 - 3x^2 + 2 $ gilt $ \large f''(x) = 6x - 6 $. Hier ist $ \large f''(0) = -6 < 0 $ (Maximum) und $ \large f''(2) = 6 > 0 $ (Minimum).

Wendepunkte

Ein Wendepunkt ist eine Stelle, an der sich die Krümmung des Graphen ändert. Das bedeutet, dass der Graph von „nach oben gewölbt“ zu „nach unten gewölbt“ oder umgekehrt wechselt. Ein Wendepunkt liegt dort, wo $ \large f''(x) = 0 $ und das Vorzeichen wechselt.

Beispiel: Für $ \large f(x) = x^3 - 3x^2 + 2 $ ist $ \large f''(x) = 6x - 6 $, was bei $ \large x = 1 $ null wird. Da das Vorzeichen wechselt, besitzt die Funktion einen Wendepunkt bei $ \large x = 1 $.

Optimierung

Die Differentialrechnung wird häufig verwendet, um Optimierungsprobleme zu lösen — also um den größten oder kleinsten Wert einer Funktion unter gegebenen Bedingungen zu finden. Dies kann zum Beispiel bedeuten, eine Fläche zu maximieren, Kosten zu minimieren oder den schnellsten Weg zu finden.

Schrittweise Vorgehensweise:

Schreibe die zu optimierende Funktion auf.
Bestimme ihre Ableitung $ \large f'(x) $.
Finde die Punkte, bei denen $ \large f'(x) = 0 $ (stationäre Punkte).
Verwende das Vorzeichen oder die zweite Ableitung, um festzustellen, ob es sich um ein Maximum oder ein Minimum handelt.

Beispiel – Optimierung

Ein Rechteck besitzt eine Fläche, die von seiner Länge $ \large x $ abhängt:

$$ \large A(x) = x(12 - 2x) = 12x - 2x^2 $$

Um die größte Fläche zu finden, wird die Funktion abgeleitet:

$$ \large A'(x) = 12 - 4x $$

Setze $ \large A'(x) = 0 $ → $ \large 12 - 4x = 0 \Rightarrow x = 3 $.

Die zweite Ableitung $ \large A''(x) = -4 $ ist negativ, also handelt es sich um ein Maximum. Das Rechteck hat somit die größte Fläche, wenn die Länge $ \large 3 $ und die Breite $ \large 12 - 2x = 6 $ beträgt.

Graphische Skizze und Interpretation

Durch die Kombination der Informationen aus $ \large f'(x) $ und $ \large f''(x) $ kann man eine genaue Grafik zeichnen, ohne einen Taschenrechner zu verwenden:

$ \large f'(x) $ zeigt, wo der Graph steigt oder fällt.
$ \large f''(x) $ zeigt, ob der Graph nach oben oder unten gekrümmt ist.
$ \large f'(x) = 0 $ liefert Hoch- und Tiefpunkte.
$ \large f''(x) = 0 $ liefert Wendepunkte.

Dies wird als vollständige Graphenanalyse bezeichnet und bildet die Grundlage sowohl für das theoretische Verständnis als auch für praktische Anwendungen von Funktionen in Wissenschaft und Technik.

Zusammenfassung

Die Ableitung ermöglicht es, das Verhalten einer Funktion zu analysieren und vorherzusagen. Mit der Differentialrechnung kann man Maxima und Minima finden, Intervalle bestimmen, in denen die Funktion steigt oder fällt, die Form des Graphen untersuchen und Optimierungsprobleme lösen. Damit ist sie eines der nützlichsten Werkzeuge der gesamten Mathematik.