Differentialgleichungen

Eine Differentialgleichung beschreibt die Beziehung zwischen einer Funktion und ihrer Ableitung. Anstatt direkt anzugeben, was die Funktion ist, beschreibt sie, wie sich die Funktion verändert. Dadurch sind Differentialgleichungen ein zentrales Werkzeug in Mathematik, Physik, Biologie und Wirtschaft, wo viele Phänomene Veränderungen über die Zeit darstellen.

 

 

Was ist eine Differentialgleichung

Eine gewöhnliche Gleichung enthält eine unbekannte Größe, zum Beispiel \( \large x \). Eine Differentialgleichung enthält dagegen eine unbekannte Funktion \( \large y(x) \) und deren Ableitungen, wie \( \large y'(x) \) oder \( \large y''(x) \). Das Ziel ist es, die Funktion \( \large y(x) \) zu finden, die die Gleichung erfüllt.

 

Beispiele:

 

$$ \large y' = 3x^2 $$

 

$$ \large y'' + y = 0 $$

 

Die erste Gleichung besagt, dass die Steigung von \( \large y \) immer \( \large 3x^2 \) beträgt. Die zweite beschreibt eine Schwingung, da sie die Funktion mit ihrer eigenen zweiten Ableitung verknüpft.

 

 

Grundidee

Eine Differentialgleichung gibt nicht direkt an, wie der Graph von \( \large y \) aussieht, sondern wie sich seine Steigung von Punkt zu Punkt ändert. Man kann sie daher als eine Art „Rezept“ für Bewegung oder Wachstum betrachten.

 

Wenn die Ableitung bekannt ist, kann man die Funktion finden, indem man das Gegenteil der Differentiation ausführt – also integriert. Daher stehen Differentialgleichungen in engem Zusammenhang mit der Integralrechnung.

 

 

Ordnung und Typen

Eine gewöhnliche Differentialgleichung (abgekürzt ODE) enthält nur eine unabhängige Variable, typischerweise \( \large x \) oder \( \large t \). Wenn die Gleichung mehrere Variablen und Ableitungen nach mehreren Variablen enthält, spricht man von einer partiellen Differentialgleichung (PDE).

 

Die Ordnung einer Differentialgleichung ist die höchste vorkommende Ableitung. Zum Beispiel:

 

• \( \large y' = 3x^2 \) → Gleichung erster Ordnung
• \( \large y'' + y = 0 \) → Gleichung zweiter Ordnung

 

 

Lösen einfacher Differentialgleichungen

Die einfachsten Differentialgleichungen können direkt durch Integration gelöst werden. Wenn zum Beispiel

 

$$ \large y' = 3x^2 $$

 

dann erhält man \( \large y(x) \), indem man die rechte Seite integriert:

 

$$ \large y = \int 3x^2 \, dx = x^3 + C $$

 

Hier ist \( \large C \) die Integrationskonstante, die alle möglichen Lösungen repräsentiert – also alle Graphen mit demselben Steigungsmuster, aber unterschiedlicher vertikaler Verschiebung.

 

 

Trennung der Variablen

Eine gängige Methode zum Lösen von Gleichungen erster Ordnung ist die Trennung der Variablen. Wenn die Gleichung in der Form

 

$$ \large \frac{dy}{dx} = g(x) \cdot h(y) $$

 

geschrieben werden kann, lassen sich \( \large x \) und \( \large y \) trennen und auf jeder Seite integrieren:

 

$$ \large \int \frac{1}{h(y)} \, dy = \int g(x) \, dx $$

 

Beispiel: Löse \( \large y' = 2xy \).

 

Trenne die Variablen: \( \large \frac{1}{y} dy = 2x dx \).

 

Integriere beide Seiten:

 

$$ \large \ln|y| = x^2 + C $$

 

Schreibe die allgemeine Lösung um:

 

$$ \large y = A e^{x^2} $$

 

wobei \( \large A = e^C \) eine Konstante ist. Diese Methode funktioniert immer dann, wenn die Variablen auf diese Weise getrennt werden können.

 

 

Lineare Differentialgleichungen erster Ordnung

Eine lineare Differentialgleichung erster Ordnung hat die Form:

 

$$ \large y' + p(x)y = q(x) $$

 

Die Lösung erhält man, indem man die gesamte Gleichung mit einem integrierenden Faktor multipliziert:

 

$$ \large \mu(x) = e^{\int p(x)\,dx} $$

 

Damit kann die Gleichung umgeschrieben werden als

 

$$ \large (\mu(x)y)' = \mu(x)q(x) $$

 

und anschließend direkt integriert werden. Diese Methode heißt Methode des integrierenden Faktors.

 

 

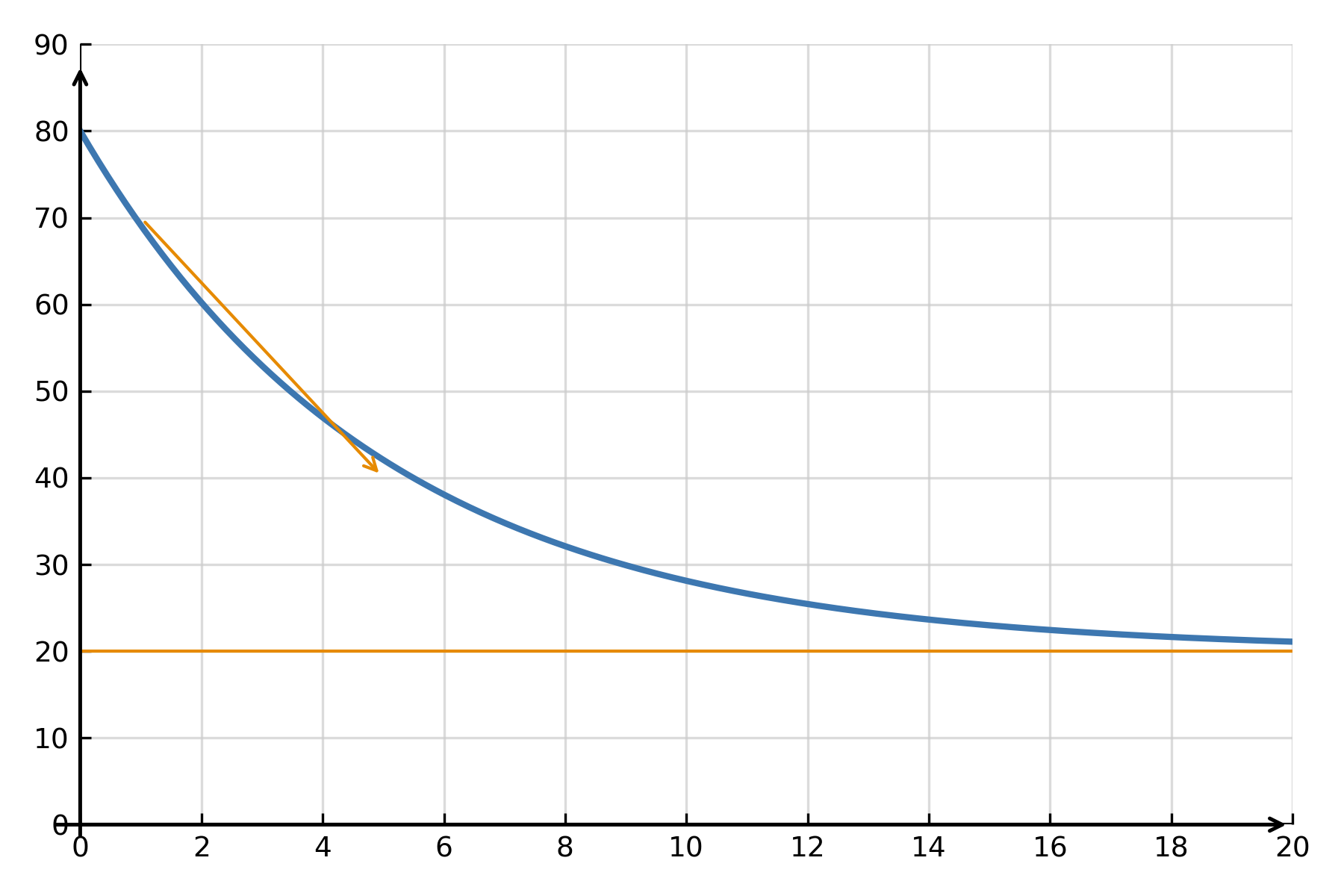
Beispiel: Newtons Abkühlungsgesetz

Ein klassisches Beispiel für eine lineare Differentialgleichung ist das Abkühlungsgesetz von Newton:

 

$$ \large \frac{dT}{dt} = -k(T - T_{\text{umg}}) $$

 

Hier beschreibt \( \large T(t) \) die Temperatur eines Körpers, der sich der Umgebungstemperatur \( \large T_{\text{umg}} \) annähert, und \( \large k \) ist eine Konstante. Die Lösung zeigt, dass sich die Temperatur exponentiell der Umgebung annähert:

 

$$ \large T(t) = T_{\text{umg}} + (T_0 - T_{\text{umg}})e^{-kt} $$

 

Eine solche Gleichung tritt auch bei radioaktivem Zerfall, der Entladung von Kondensatoren und ökonomischen Anpassungsmodellen auf.

 

 

 

Differentialgleichungen zweiter Ordnung

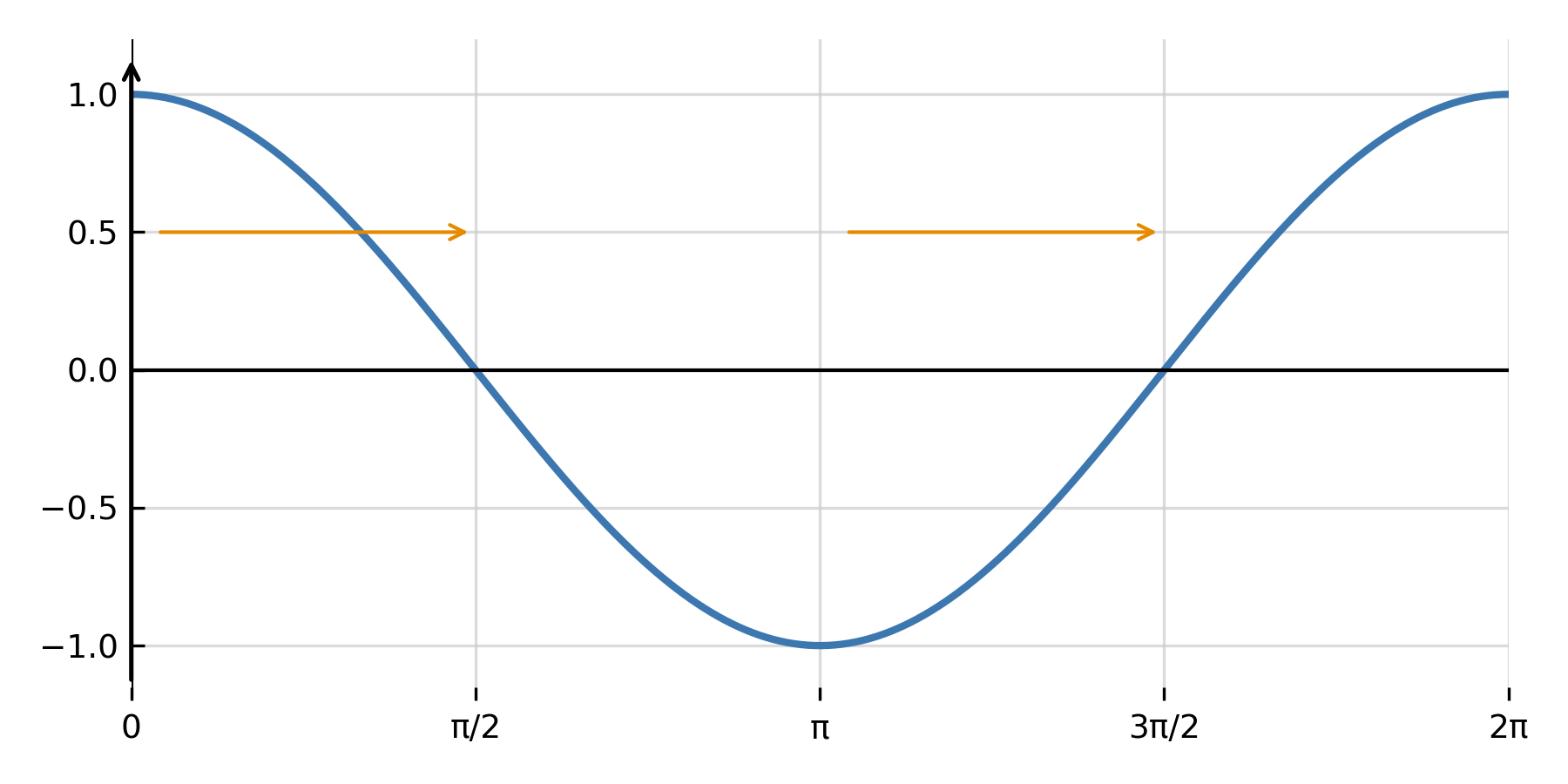
Wenn die zweite Ableitung vorkommt, beschreibt die Gleichung häufig Bewegung oder Schwingungen. Ein wichtiges Beispiel ist die harmonische Schwingung:

 

$$ \large y'' + \omega^2 y = 0 $$

 

Die Lösung ist eine Kombination aus Sinus und Kosinus:

 

$$ \large y = A \cos(\omega x) + B \sin(\omega x) $$

 

Hier geben \( \large A \) und \( \large B \) die Anfangsbedingungen an, während \( \large \omega \) die Schwingungsfrequenz beschreibt. Diese Art von Gleichung wird in der Mechanik, in der Wellentheorie und in elektrischen Schaltkreisen verwendet.

 

 

 

Numerische Lösungen

In vielen Fällen kann eine Differentialgleichung nicht analytisch gelöst werden. Stattdessen werden numerische Methoden verwendet, bei denen die Funktion Punkt für Punkt aus ihrer Ableitung berechnet wird. Die bekanntesten Methoden sind das Euler-Verfahren, das Runge–Kutta-Verfahren und die Sekantenmethode, die alle im Abschnitt Numerische Methoden erläutert werden.

 

 

Zusammenfassung

Differentialgleichungen beschreiben, wie sich Funktionen verändern, und spielen eine zentrale Rolle in der angewandten Mathematik. Sie werden verwendet, um Wachstum, Bewegung, Schwingungen, Wärme, Strom und viele andere Phänomene zu modellieren. Einige lassen sich per Hand lösen, andere erfordern numerische Methoden, aber alle verbinden die Differential- und Integralrechnung zu einem einheitlichen System.