Vektortyper og roller

Vektorer kan have forskellige roller afhængigt af sammenhængen. Nogle bruges til at beskrive retninger, andre til at angive en vinkelret retning eller til at danne grundlag for et helt koordinatsystem. Her ser vi på de vigtigste vektortyper.

 

 

Retningsvektorer

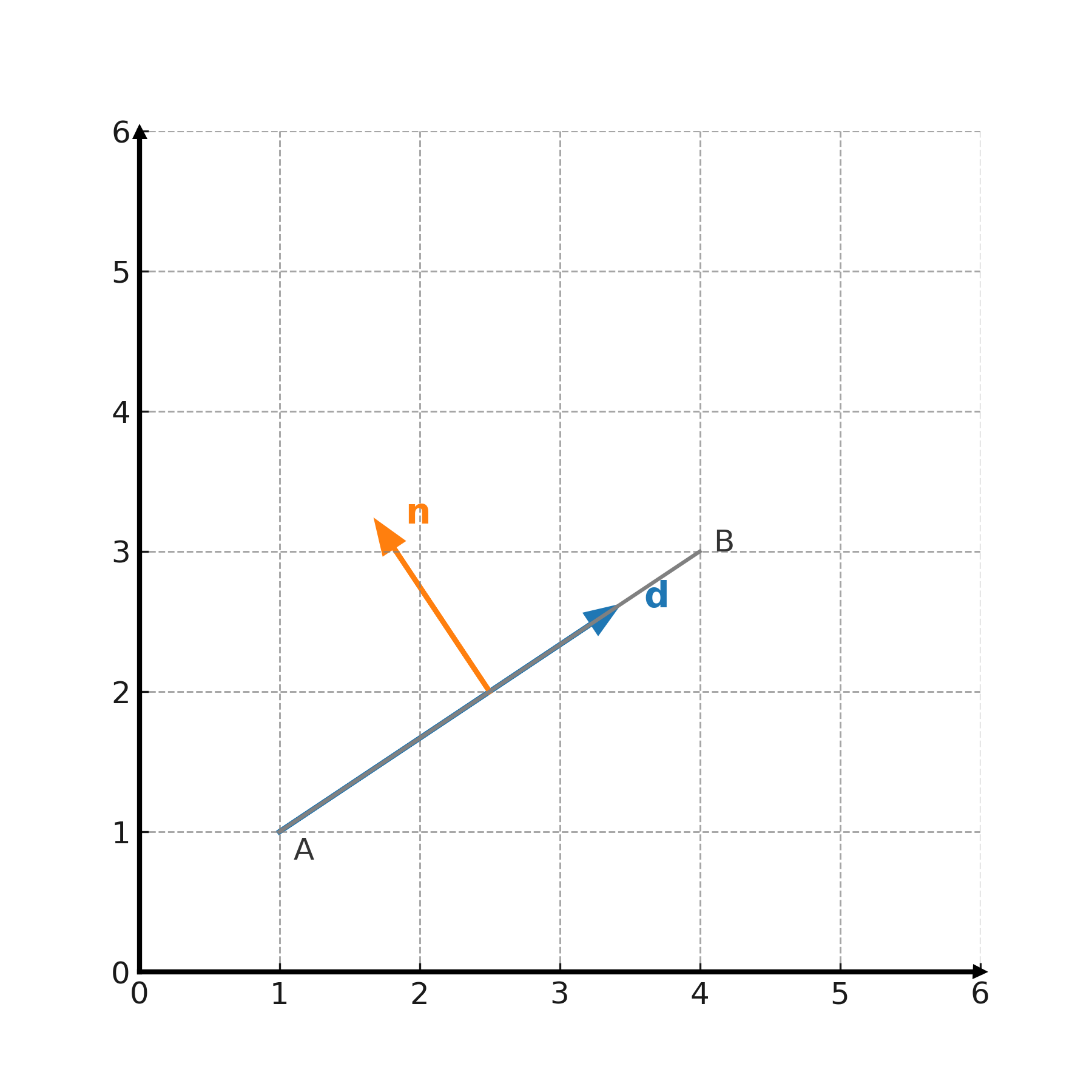
En retningsvektor (d) beskriver retningen af en linje eller et plan. Hvis en linje går gennem punkterne \( \large A=(x_1,y_1) \) og \( \large B=(x_2,y_2) \), så er

 

$$ \large \mathbf{d} = (x_2-x_1,\; y_2-y_1) $$

 

en retningsvektor for linjen. Med en retningsvektor kan man skrive en parameterfremstilling:

 

$$ \large (x,y) = (x_1,y_1) + t \cdot \mathbf{d}, \quad t \in \mathbb{R} $$

 

hvilket beskriver alle punkterne på linjen.

 

 

Normalvektorer

En normalvektor står vinkelret på en linje eller et plan. Hvis linjen har retningsvektor \( \large (a,b) \), så er

 

$$ \large \mathbf{n} = (-b,a) \quad \text{eller} \quad (b,-a) $$

 

normalvektorer. En normalvektor kan bruges til at skrive en linje på formen

 

$$ \large n_1 \cdot x + n_2 \cdot y + c = 0 $$

 

hvor \( \large (n_1,n_2) \) er normalvektoren. At en vektor er normal kan testes ved hjælp af skalarproduktet: Hvis \( \large \mathbf{r} \cdot \mathbf{n} = 0 \), så er de vinkelrette.

 

 

Enhedsvektorer

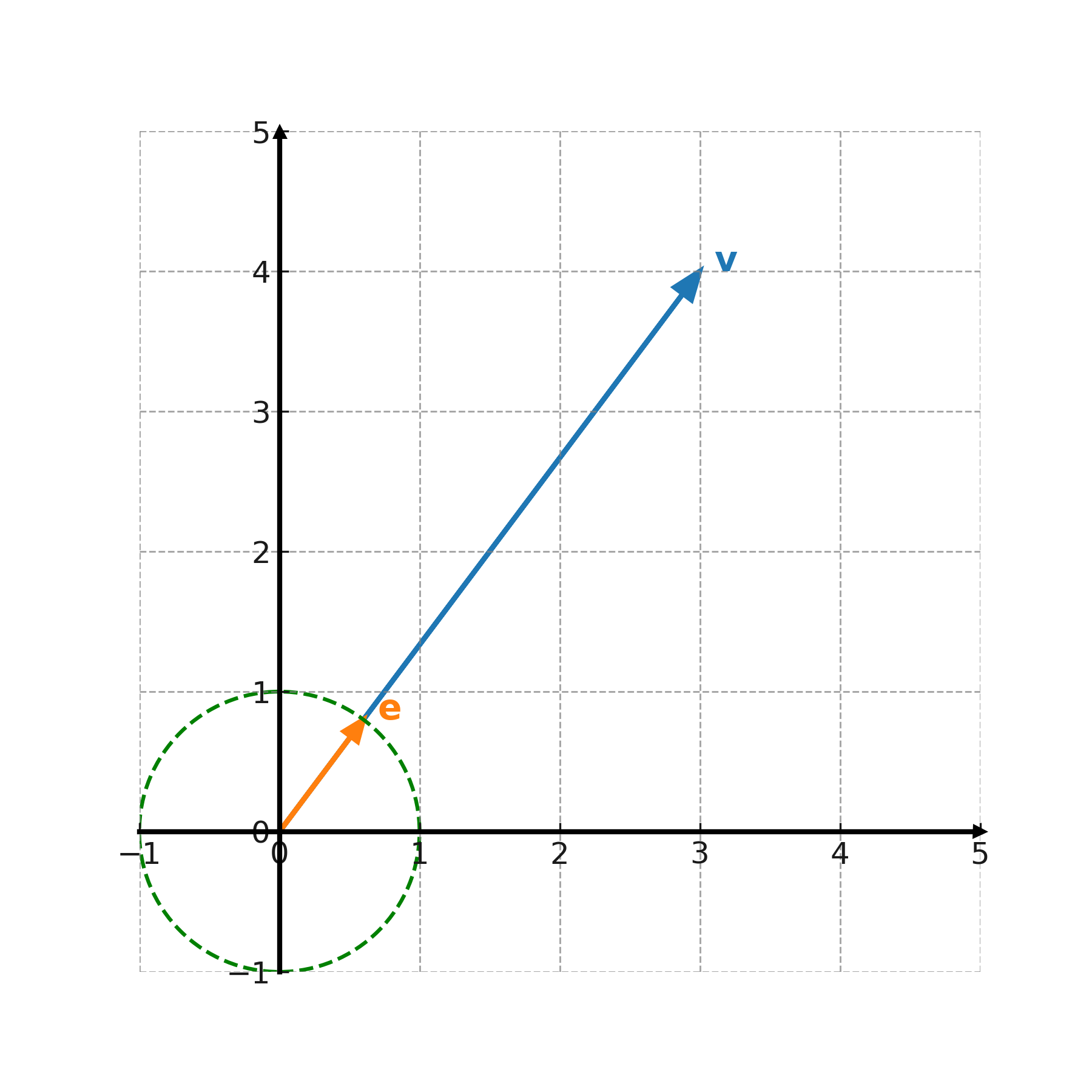
En enhedsvektor har længde 1 og bruges til at beskrive en ren retning. Enhver vektor kan gøres til en enhedsvektor ved at dividere med sin længde:

 

$$ \large \mathbf{e} = \frac{1}{|\mathbf{v}|} \cdot \mathbf{v} $$

 

Enhedsvektorer bruges fx til at definere retningen af akserne i et koordinatsystem.

 

 

Tangentvektorer

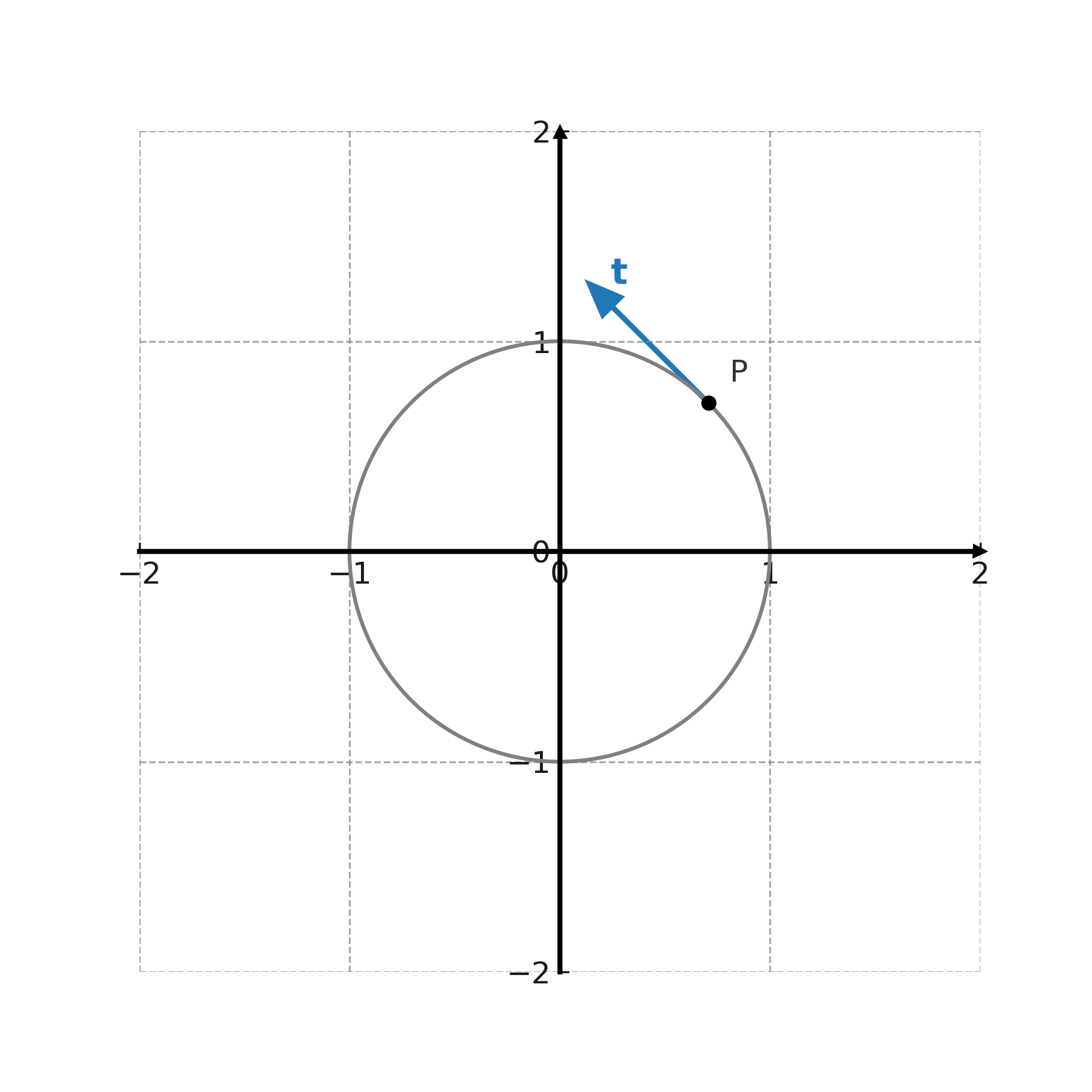
I forbindelse med kurver bruges tangentvektorer til at beskrive retningen i et bestemt punkt. For en differentiabel kurve \( \large (x(t),y(t)) \) er tangentvektoren givet ved

 

$$ \large \mathbf{t} = \big(x'(t),\,y'(t)\big) $$

 

som viser, hvordan kurven bevæger sig i punktet.

 

Basisvektorer

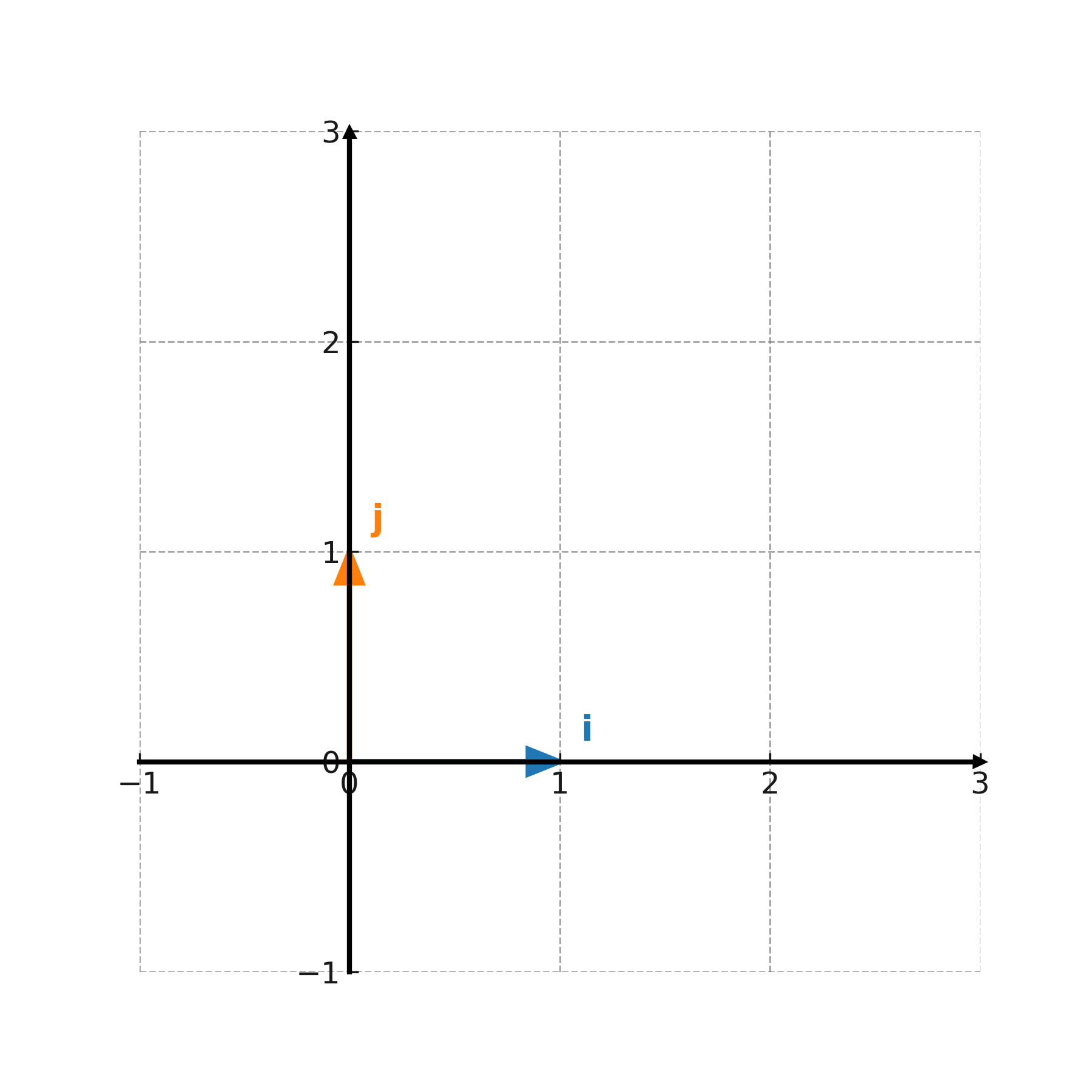
I et koordinatsystem bruges basisvektorer til at beskrive alle andre vektorer. I planen er standardbasis

 

$$ \large \mathbf{i} = (1,0), \quad \mathbf{j} = (0,1) $$

 

Hver vektor kan skrives som en kombination af disse: \( \large \mathbf{v} = x \cdot \mathbf{i} + y \cdot \mathbf{j} \).

 

Opsamling

Retningsvektorer bruges til at angive retninger af linjer og planer, normalvektorer til at angive vinkelrette retninger, enhedsvektorer til at isolere ren retning, tangentvektorer til at beskrive kurvers forløb, og basisvektorer til at opbygge hele koordinatsystemer. Sammen danner de grundlaget for, hvordan vektorer anvendes i både geometri og algebra.