Inverse funktioner

En funktion er bijektiv, hvis den er både injektiv og surjektiv.

Det betyder, at hvert element i definitionsmængden $ \large A$ svarer til præcis ét element i målmængden $ \large B$, og at hele $ \large B$ dækkes.

Dermed findes der en entydig sammenhæng, som kan vendes om.

Definition

En funktion $ \large f : A \to B$ er bijektiv, hvis:

$$ \large \forall a_1,a_2 \in A: f(a_1)=f(a_2) \Rightarrow a_1=a_2 \quad (\text{injektivitet}) $$

$$ \large \forall b \in B \;\exists a \in A : f(a)=b \quad (\text{surjektivitet}) $$

Kombinationen af de to egenskaber sikrer, at funktionen kan "vendes om".

Eksistens af invers funktion

Hvis $ \large f : A \to B$ er bijektiv, findes der en invers funktion $ \large f^{-1} : B \to A$, som opfylder:

$$ \large f^{-1}(f(a)) = a \quad \text{for alle } a \in A $$

$$ \large f(f^{-1}(b)) = b \quad \text{for alle } b \in B $$

Inversen "ophæver" virkningen af den oprindelige funktion.

Eksempler

Bijektiv funktion: $ \large f(x)=x+3$ fra $ \large \mathbb{Z} \to \mathbb{Z}$ er bijektiv.

Den inverse funktion er $ \large f^{-1}(y)=y-3$.

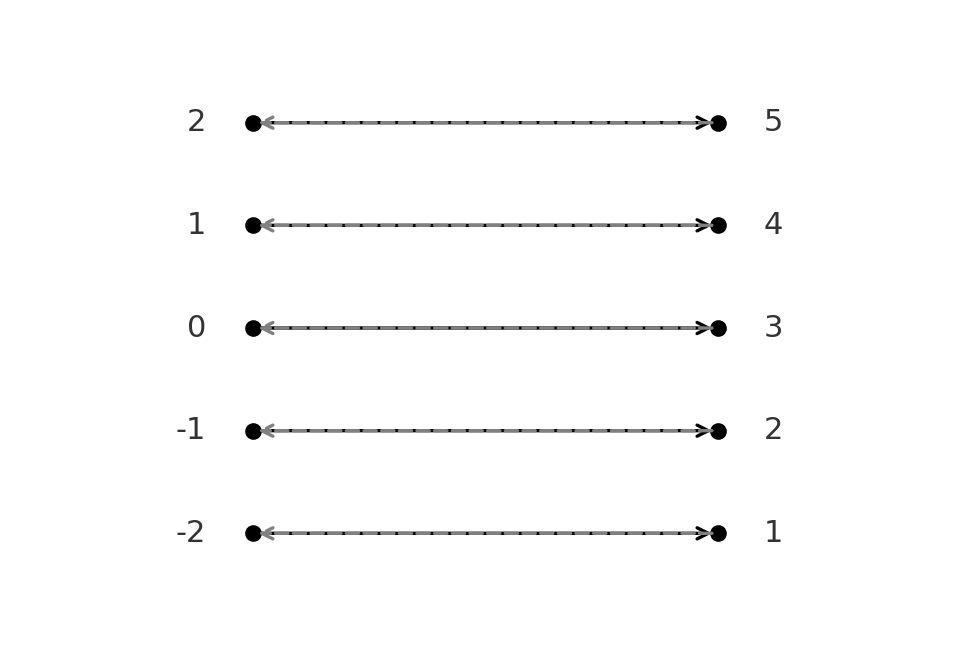
Bijektiv invers funktion

Ikke-bijektiv funktion: $ \large f(x)=x^2$ fra $ \large \mathbb{R} \to \mathbb{R}$ er ikke bijektiv, fordi den ikke er injektiv (både $ \large -2$ og $ \large 2$ giver billedet $ \large 4$).

Derfor findes der ingen invers funktion her.

Anvendelse

Bijektive funktioner og deres inverse spiller en central rolle i mange områder af matematik og datalogi:

Kryptografi: Krypteringsalgoritmer kræver funktioner, der kan vendes om entydigt, så beskeder kan dekrypteres igen.
Algebra: Isomorfier mellem algebraiske strukturer er bijektioner, der bevarer strukturen.
Logik og teori: I matematiske beviser bruges bijektioner til at sammenligne størrelsen af mængder (kardinalitet).

At forstå bijektive funktioner er derfor afgørende for både teoretiske og praktiske anvendelser.