Eksempler på funktioner
For bedre at forstå funktioners egenskaber ser vi her på konkrete eksempler i de klassiske talmængder: de naturlige tal \( \large \mathbb{N}\), heltallene \( \large \mathbb{Z}\) og de reelle tal \( \large \mathbb{R}\).
Eksempel 1: Injektiv funktion i \( \large \mathbb{N}\)
Funktionen \( \large f : \mathbb{N} \to \mathbb{N}\) givet ved \( \large f(n) = 2n\).
$$ \large f(n) = 2n $$
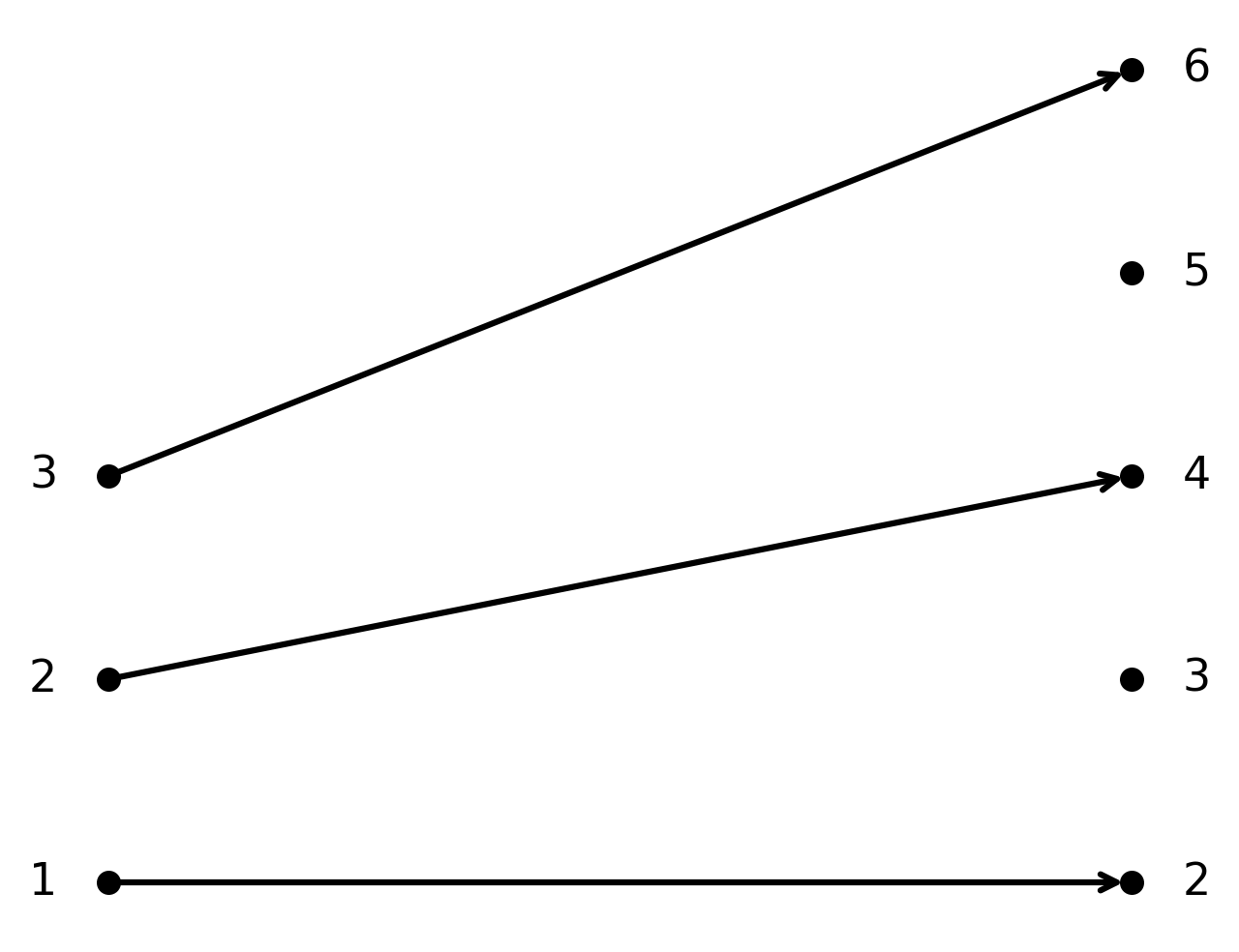
Her er \( f\) injektiv, fordi to forskellige naturlige tal altid giver forskellige resultater, når de ganges med 2. Men funktionen er ikke surjektiv, da ulige tal ikke rammes.
Eksempel 2: Surjektiv funktion i \( \large \mathbb{Z}\)
Funktionen \( \large f : \mathbb{Z} \to \mathbb{Z}\) givet ved \( \large f(n) = \lfloor \tfrac{n}{2} \rfloor\).
$$ \large f(n) = \left\lfloor \frac{n}{2} \right\rfloor $$
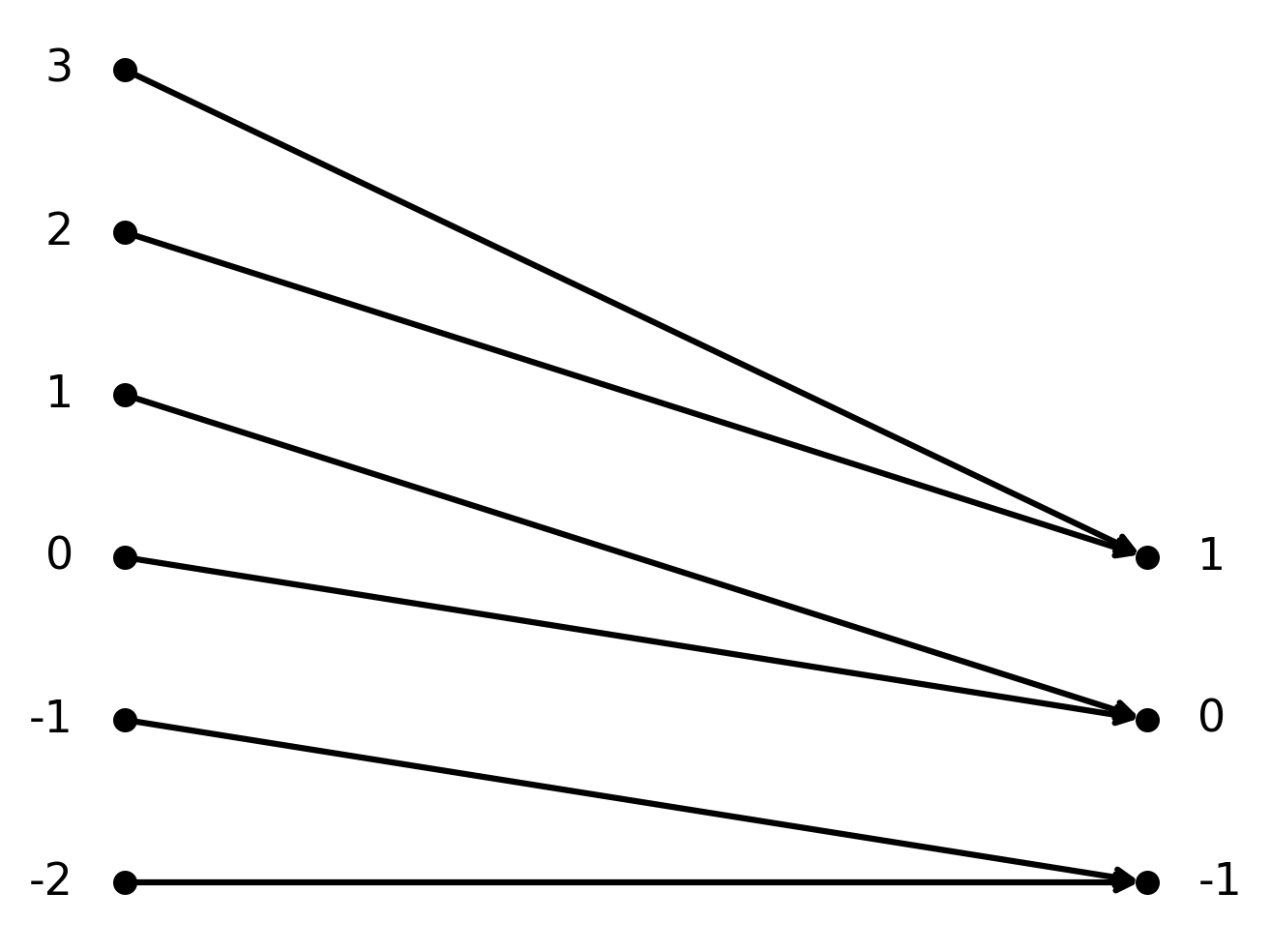
Her er funktionen surjektiv, fordi hvert heltal rammes af mindst ét \( \large n\). For eksempel giver \(\large f(2)=1\) og \(\large f(3)=1\).
Til gengæld er funktionen ikke injektiv, fordi flere input kan give samme output.
Eksempel 3: Bijektiv funktion i \( \large \mathbb{Z}\)
Funktionen \( \large f : \mathbb{Z} \to \mathbb{Z}\) givet ved \( \large f(n) = n+1\).
$$ \large f(n) = n+1 $$

Her er \(\large f\) bijektiv: hvert heltal får et unikt output, og alle heltal rammes.
Dermed kan funktionen vendes om med en invers \(\large f^{-1}(n) = n-1\).
Eksempel 4: Funktioner i \( \large \mathbb{R}\)
I de reelle tal kan vi finde mange funktioner, der illustrerer egenskaberne:
- \( \large f(x) = x^3 \) fra \( \large \mathbb{R} \to \mathbb{R}\) er bijektiv. Hvert reelt tal har et unikt billede, og hele \( \large \mathbb{R}\) bliver dækket.
- \( \large f(x) = x^2 \) fra \( \large \mathbb{R} \to \mathbb{R}\) er ikke injektiv (fordi \( f(2)=f(-2)\)), men den er surjektiv, hvis man kun ser på \( \large [0,\infty[\) som målmængde.
- \( \large f(x) = e^x \) fra \( \large \mathbb{R} \to (0,\infty)\) er bijektiv, fordi alle positive reelle tal rammes entydigt.
Opsummering
Eksemplerne viser, at funktioners egenskaber afhænger af:
- Hvilke mængder vi betragter som definition og målmængde.
- Hvordan funktionen kobler input og output.
De klassiske talmængder \( \large \mathbb{N}, \mathbb{Z}, \mathbb{R}\) giver mange gode og enkle eksempler på injektive, surjektive og bijektive funktioner.