Injektive, surjektive og bijektive funktioner
I matematik kan funktioner have forskellige egenskaber alt efter, hvordan elementerne i definitionsmængden og målmængden forbindes.
De tre vigtigste er injektiv, surjektiv og bijektiv.
Injektiv funktion
En funktion \( \large f : A \to B\) er injektiv, hvis to forskellige elementer i \( \large A\) altid får forskellige billeder i \( \large B\).
Med andre ord:
$$ \large f(a_1) = f(a_2) \;\Rightarrow\; a_1 = a_2 $$
Eksempel:
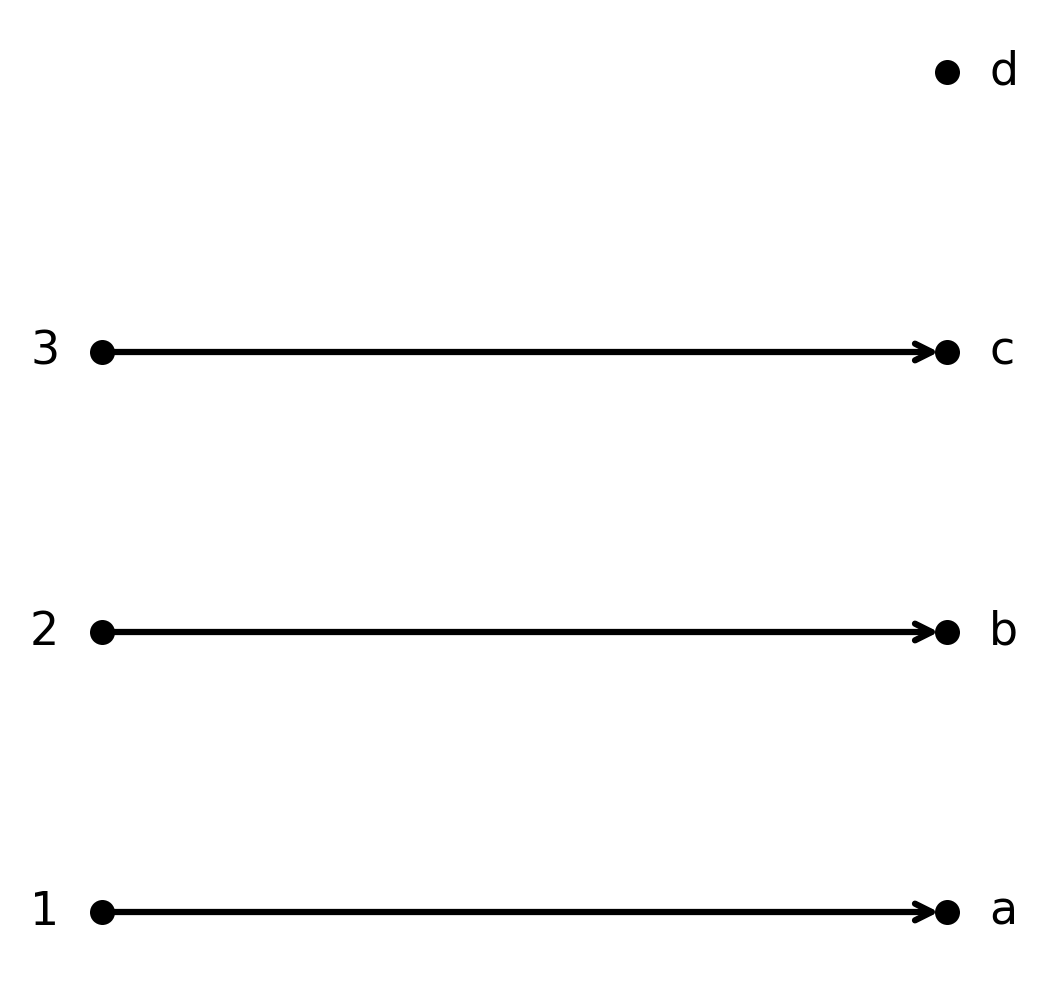
Funktionen \( \large f : \{1,2,3\} \to \{a,b,c,d\}\) givet ved \( \large f(1)=a, f(2)=b, f(3)=c\) er injektiv.
Hvert element i \( \large A\) rammer et unikt element i \( \large B\), men ikke hele målmængden bliver dækket.
Surjektiv funktion
En funktion \( \large f : A \to B\) er surjektiv, hvis hvert element i \( \large B\) rammes af mindst ét element fra \( \large A\).
Altså:
$$ \large \forall b \in B, \;\exists a \in A : f(a) = b $$
Eksempel:
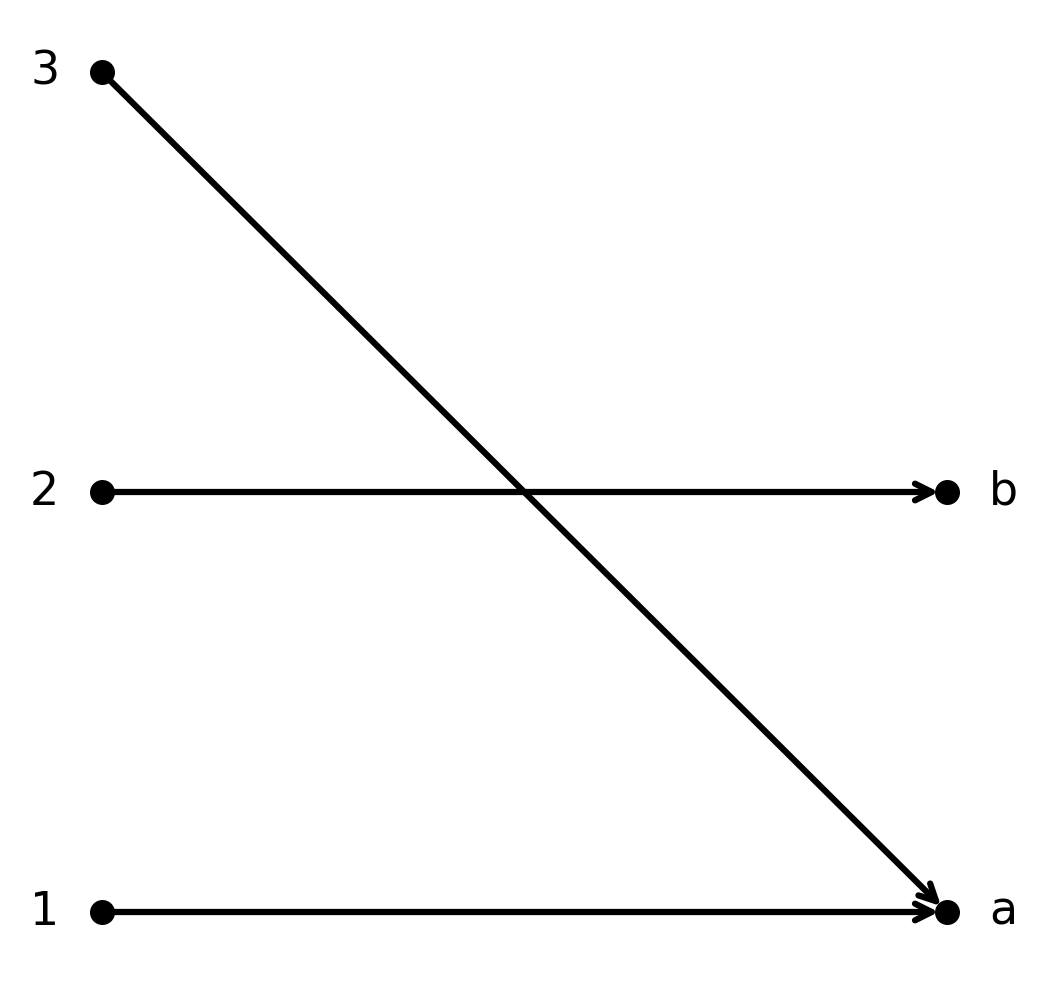
Funktionen \( \large f : \{1,2,3\} \to \{a,b\}\) givet ved \( \large f(1)=a, f(2)=b, f(3)=a\) er surjektiv.
Begge elementer i \( \large B\) bliver ramt, men funktionen er ikke injektiv, fordi \( \large 1\) og \( \large 3\) begge rammer \( \large a\).
Bijektiv funktion
En funktion er bijektiv, hvis den er både injektiv og surjektiv.
Det betyder, at der er en entydig sammenhæng mellem elementerne i \( \large A\) og \( \large B\). Hvert element i \( \large A\) rammer et unikt element i \( \large B\), og hele \( \large B\) bliver dækket.
Eksempel:
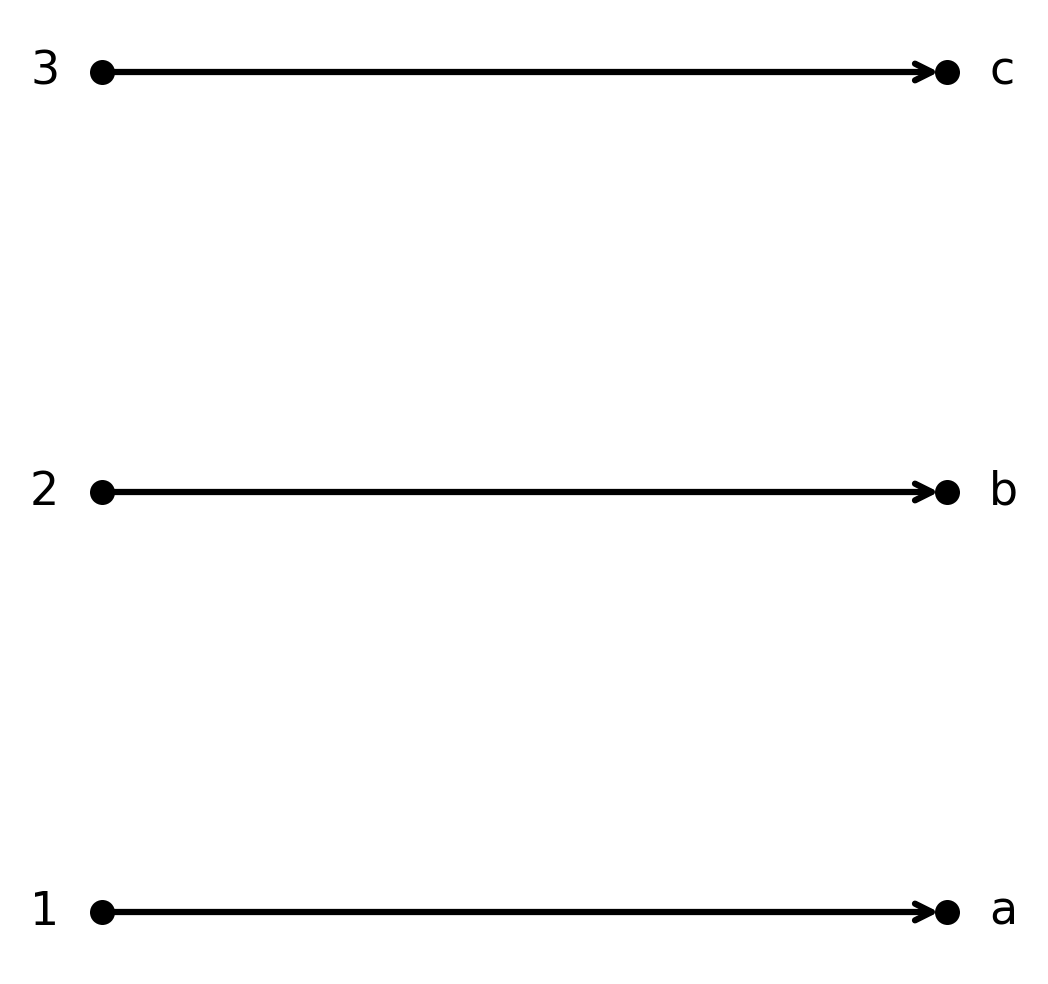
Funktionen \( \large f : \{1,2,3\} \to \{a,b,c\}\) givet ved \( \large f(1)=a, f(2)=b, f(3)=c\) er bijektiv.
Hvert element i \( \large A\) kobles til et unikt element i \( \large B\), og alle elementer i \( \large B\) bliver ramt.
Opsummering
- Injektiv: To forskellige input giver altid forskellige output.
- Surjektiv: Hele målmængden bliver dækket.
- Bijektiv: Kombination af de to – der findes en entydig kobling, som kan vendes om.
Bijektive funktioner er særligt vigtige, fordi de altid har en invers funktion, hvilket gør det muligt at gå tilbage fra output til input.