Probabilité statistique

La probabilité peut être calculée de deux manières : théorique (classique) et statistique (empirique).

 

Probabilité classique

Si l’on connaît l’univers des résultats et que tous les résultats sont également probables, on peut utiliser la formule :

 

$$ \large P(A) = \frac{\text{nombre de résultats favorables}}{\text{nombre de résultats possibles}} $$

 

Exemple : La probabilité d’obtenir un six avec un dé est :

 

$$ \large \frac{1}{6} \approx 0.167 = 16.7\% $$

 

 

Probabilité statistique (empirique)

Parfois, on ne peut pas calculer la probabilité directement. On réalise alors des essais ou des expériences et on utilise les observations pour calculer la probabilité.

 

Exemple : Nous lançons un dé 1.000 fois et nous notons fréquence absolue et relative :

 

	1	2	3	4	5	6
$$ h(x) $$	$$ 180 $$	$$ 176 $$	$$ 149 $$	$$ 170 $$	$$ 167 $$	$$ 158 $$
$$ f(x) $$	$$ \tfrac{180}{1000} $$	$$ \tfrac{176}{1000} $$	$$ \tfrac{149}{1000} $$	$$ \tfrac{170}{1000} $$	$$ \tfrac{167}{1000} $$	$$ \tfrac{158}{1000} $$
Attendu	$$ \tfrac{1000}{6} \approx 167 $$	$$ 167 $$	$$ 167 $$	$$ 167 $$	$$ 167 $$	$$ 167 $$

 

 

Diagramme

Le diagramme en barres ci-dessous montre la probabilité théorique (167 pour chaque face) comparée aux résultats empiriques.

 

 

 

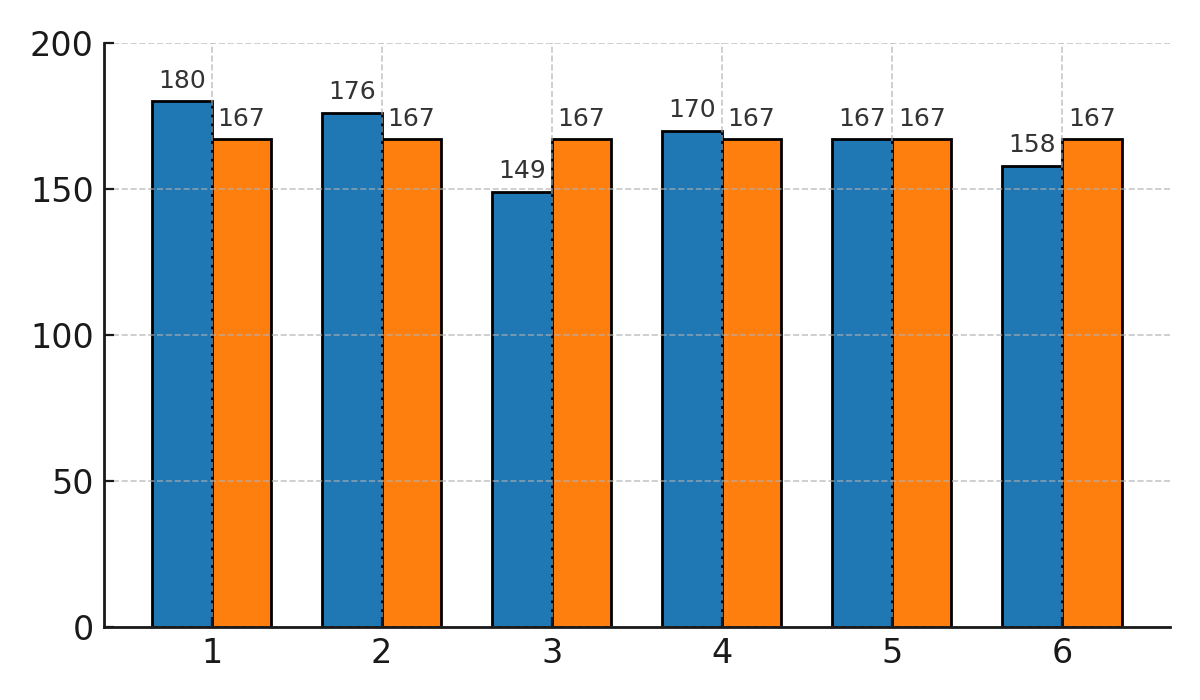
Comparaison

Nous savons que la probabilité d’obtenir un six est :

 

$$ \large \tfrac{1}{6} \approx 0.167 = 16.7\% $$

 

Notre expérience a montré à la place :

 

$$ \large \tfrac{158}{1000} = 0.158 = 15.8\% $$

 

Le résultat n’est pas exactement le même que la valeur théorique, mais il est proche. Cela montre comment la probabilité statistique est utilisée pour approcher la probabilité théorique à travers des observations.

 

La probabilité statistique est donc un outil pratique lorsqu’on ne peut pas calculer directement la probabilité, mais qu’on doit se baser sur des observations.