Loi des grands nombres

La loi des grands nombres est un principe fondamental de la théorie des probabilités.

Elle dit que plus on répète une expérience, plus les résultats observés se rapprochent de la probabilité théorique.

 

 

Exemple avec un dé

Si l’on lance un dé une seule fois, rien ne garantit d’obtenir un six.

Si on le lance 6 fois, il est tout à fait possible qu’aucun six n’apparaisse.

Si on le lance 1.000 fois, on constatera généralement qu’environ un sixième des lancers donne un six – soit environ 167 fois.

 

 

Probabilité théorique

Nous savons que la probabilité d’obtenir un six est :

 

$$ P(\text{six}) = \tfrac{1}{6} \approx 0,167 = 16,7\% $$

 

Probabilité statistique

Dans une expérience avec 1.000 lancers, on peut obtenir le résultat :

 

• Nombre de six : 158
• Probabilité statistique : \( \tfrac{158}{1000} = 0,158 = 15,8\% \)

 

Cela est proche de la valeur théorique de 16,7 %.

 

 

 

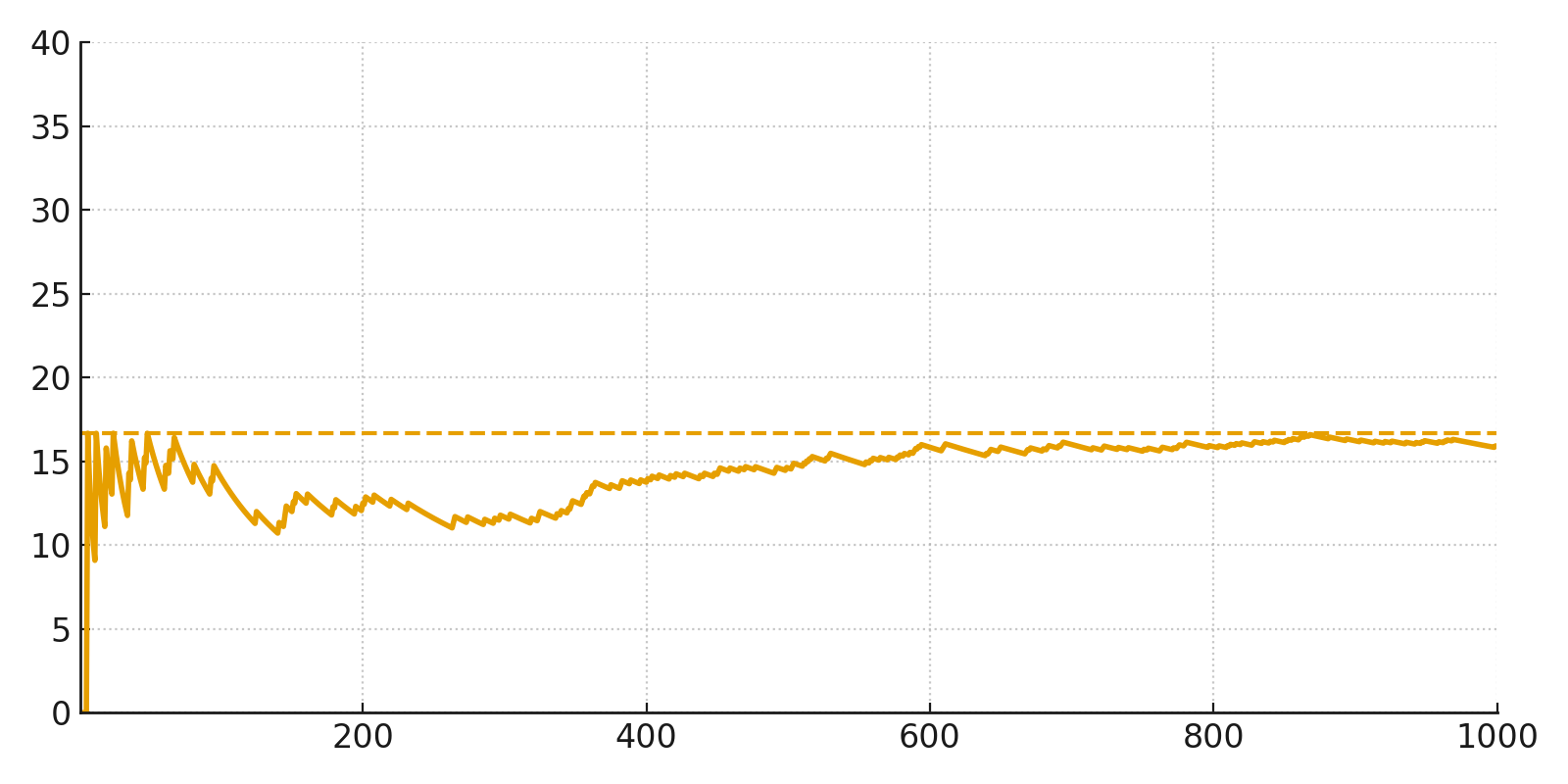
Ici nous avons lancé un dé 1.000 fois et suivi le pourcentage de lancers ayant donné un six.

Au début la courbe fluctue beaucoup, mais à mesure que le nombre de lancers augmente, elle se stabilise autour de la probabilité théorique d’environ 16,7 %.

C’est exactement ce que montre la loi des grands nombres : les probabilités n’ont de sens que lorsqu’on dispose de nombreuses observations.

 

 

Importance

La loi des grands nombres montre pourquoi les probabilités ont un sens en pratique :

 

• Les petits ensembles de données peuvent donner des fluctuations aléatoires.
• Les grands ensembles de données donnent une image plus fiable.

 

 

Résumé

• La loi des grands nombres s’applique à de nombreuses répétitions d’une expérience.
• Les fréquences empiriques se rapprochent des probabilités théoriques.
• Plus l’échantillon est grand, plus le résultat est précis.