Les opérations sur les ensembles sont des méthodes pour combiner ou comparer des ensembles. Ici, nous examinons l’union, l’intersection, les ensembles disjoints, la différence, le complément et la façon dont ces notions peuvent être visualisées avec des diagrammes de Venn.

 

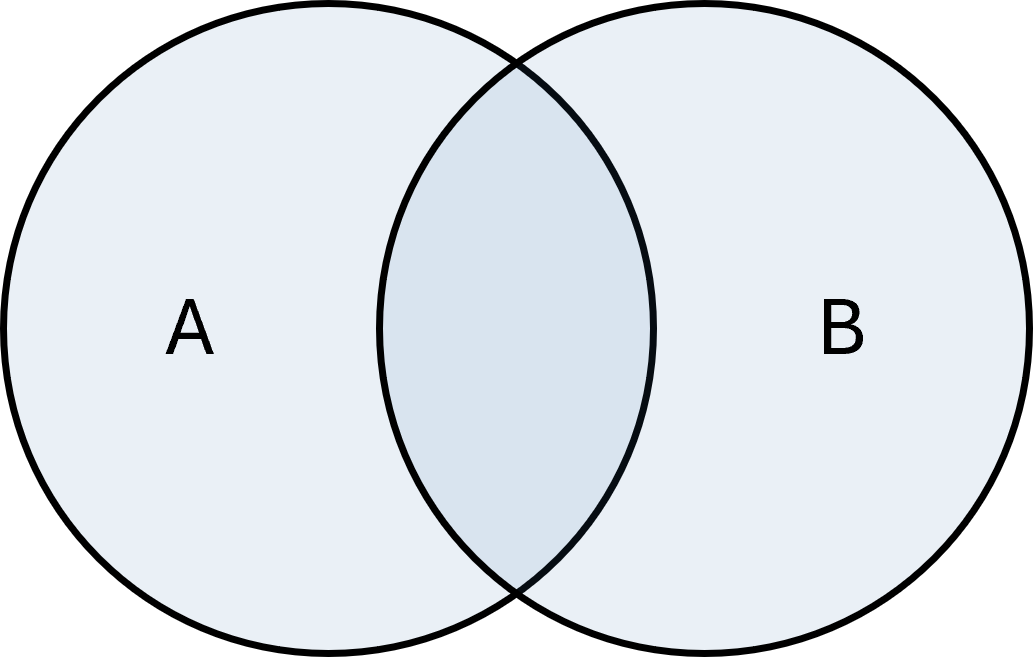
Union

L’union de deux ensembles \( \large A\) et \( \large B\) est l’ensemble de tous les éléments qui appartiennent à \( \large A\), à \( \large B\) ou aux deux. Elle s’écrit :

 

$$ \large A \cup B = \{x \mid x \in A \;\vee\; x \in B\} $$

 

Exemple : Si \( \large A = \{1,2,3\}\) et \( \large B = \{3,4,5\}\), alors \( \large A \cup B = \{1,2,3,4,5\}\).

 

 

 

 

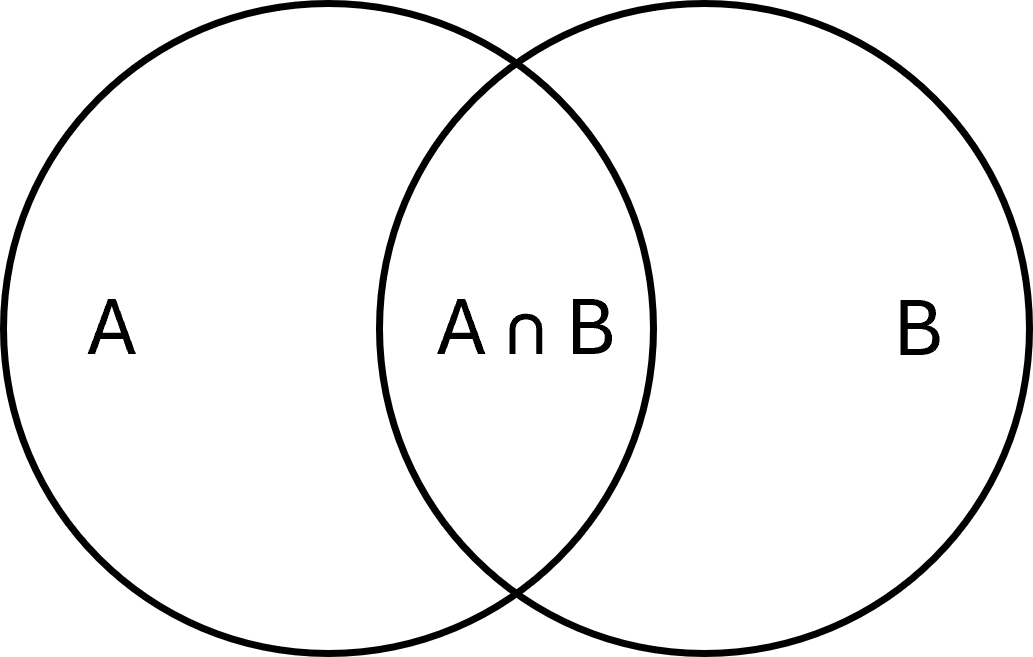
Intersection

L’intersection de deux ensembles est l’ensemble des éléments qu’ils ont en commun. Elle s’écrit :

 

$$ \large A \cap B = \{x \mid x \in A \;\wedge\; x \in B\} $$

 

Exemple : Si \( \large A = \{1,2,3\}\) et \( \large B = \{3,4,5\}\), alors \( \large A \cap B = \{3\}\).

 

 

 

 

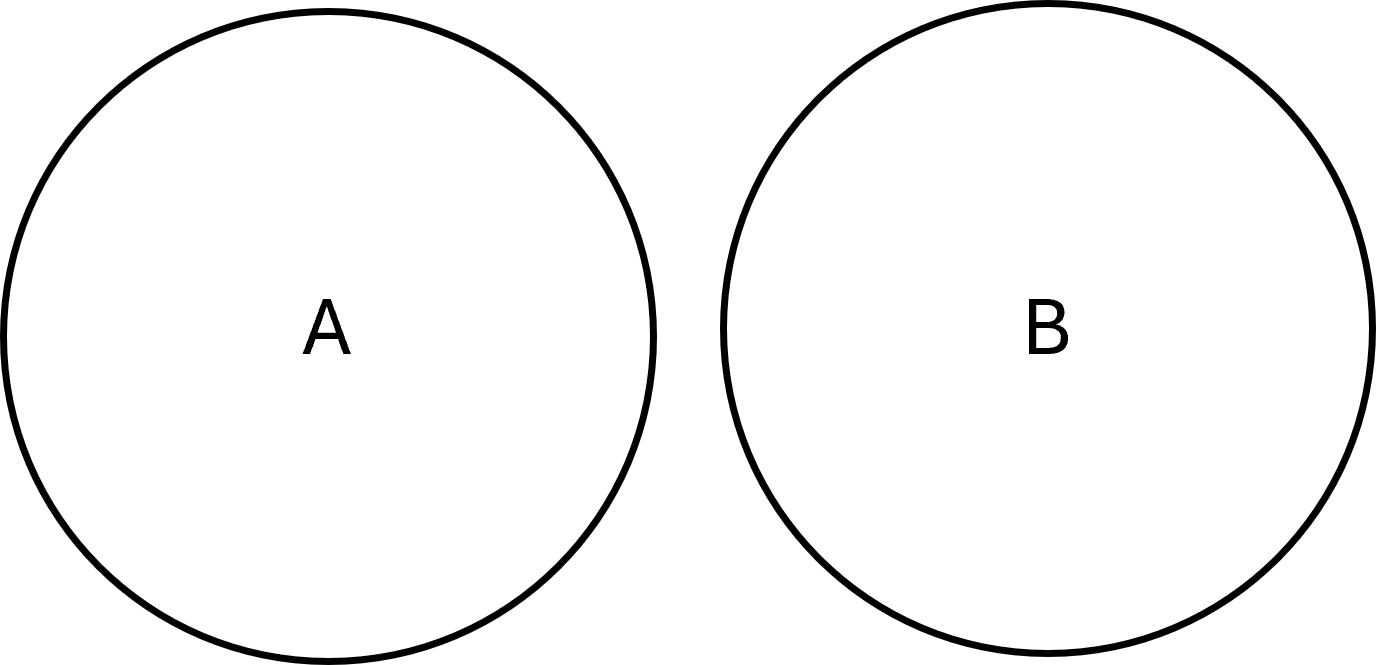
Ensembles disjoints

Deux ensembles sont disjoints s’ils n’ont aucun élément en commun. C’est-à-dire que leur intersection est vide :

 

$$ \large A \cap B = \emptyset $$

 

Exemple : \( \large A = \{1,2,3\}, B = \{4,5,6\}\).

 

 

 

 

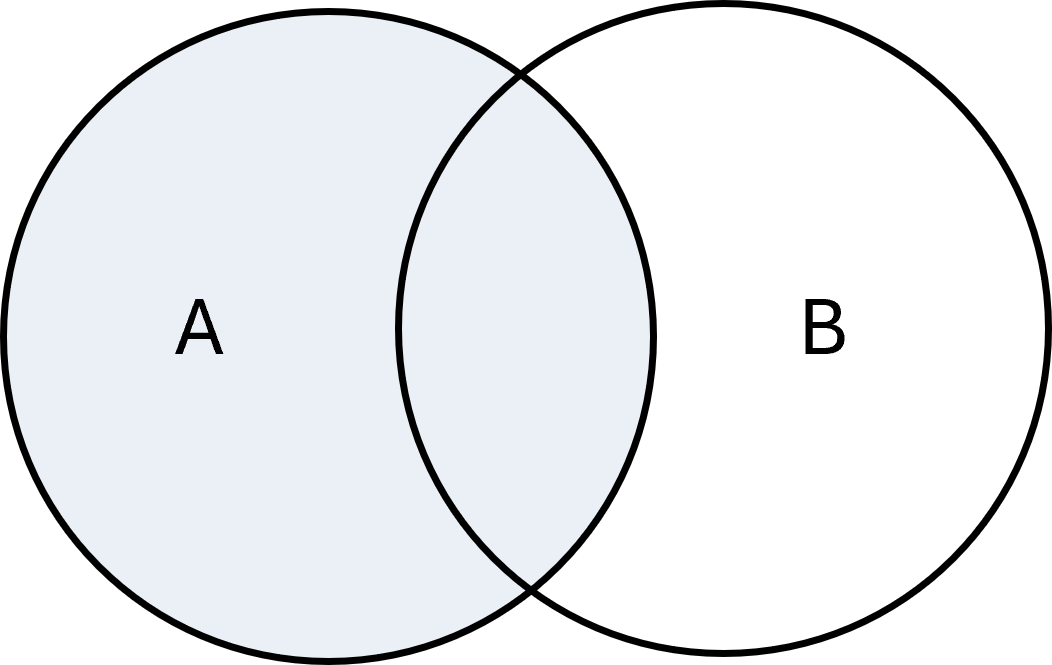
Différence

La différence de deux ensembles \( \large A\) et \( \large B\), notée \( \large A - B\) ou \( \large A \setminus B\), est l’ensemble des éléments qui appartiennent à \( \large A\) mais pas à \( \large B\) :

 

$$ \large A - B = \{x \mid x \in A \;\wedge\; x \notin B\} $$

 

Exemple : Si \( \large A = \{1,2,3\}, B = \{3,4,5\}\), alors \( \large A - B = \{1,2\}\).

 

 

 

 

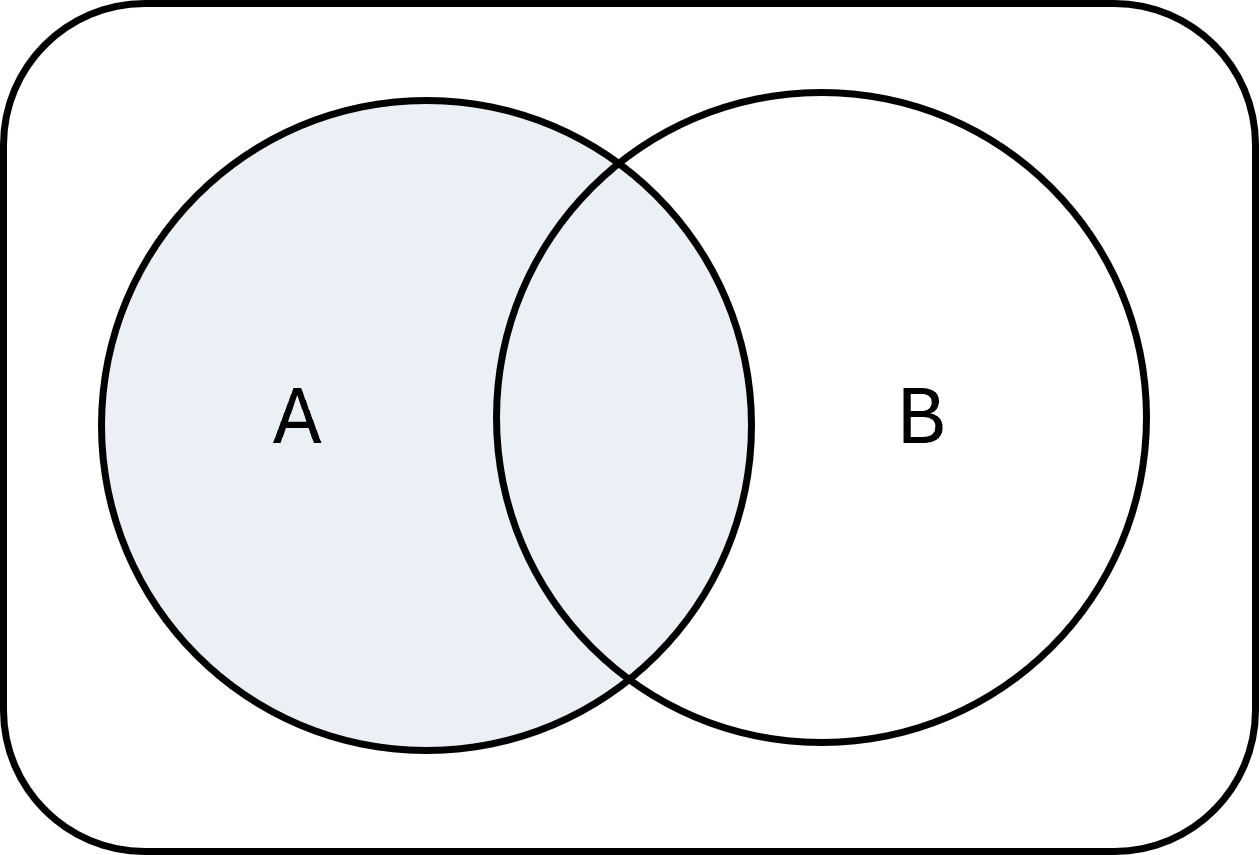
Complément

Si nous avons un univers \( \large U\) qui contient tous les éléments possibles, nous pouvons définir le complément d’un ensemble \( \large A\) comme l’ensemble de tous les éléments de \( \large U\) qui ne sont pas dans \( \large A\). Il s’écrit :

 

$$ \large A^{c} = \{x \in U \mid x \notin A\} $$

 

Exemple : Si \( \large U = \{1,2,3,4,5\}\) et \( \large A = \{1,2\}\), alors \( \large A^{c} = \{3,4,5\}\).

 

 

 

 

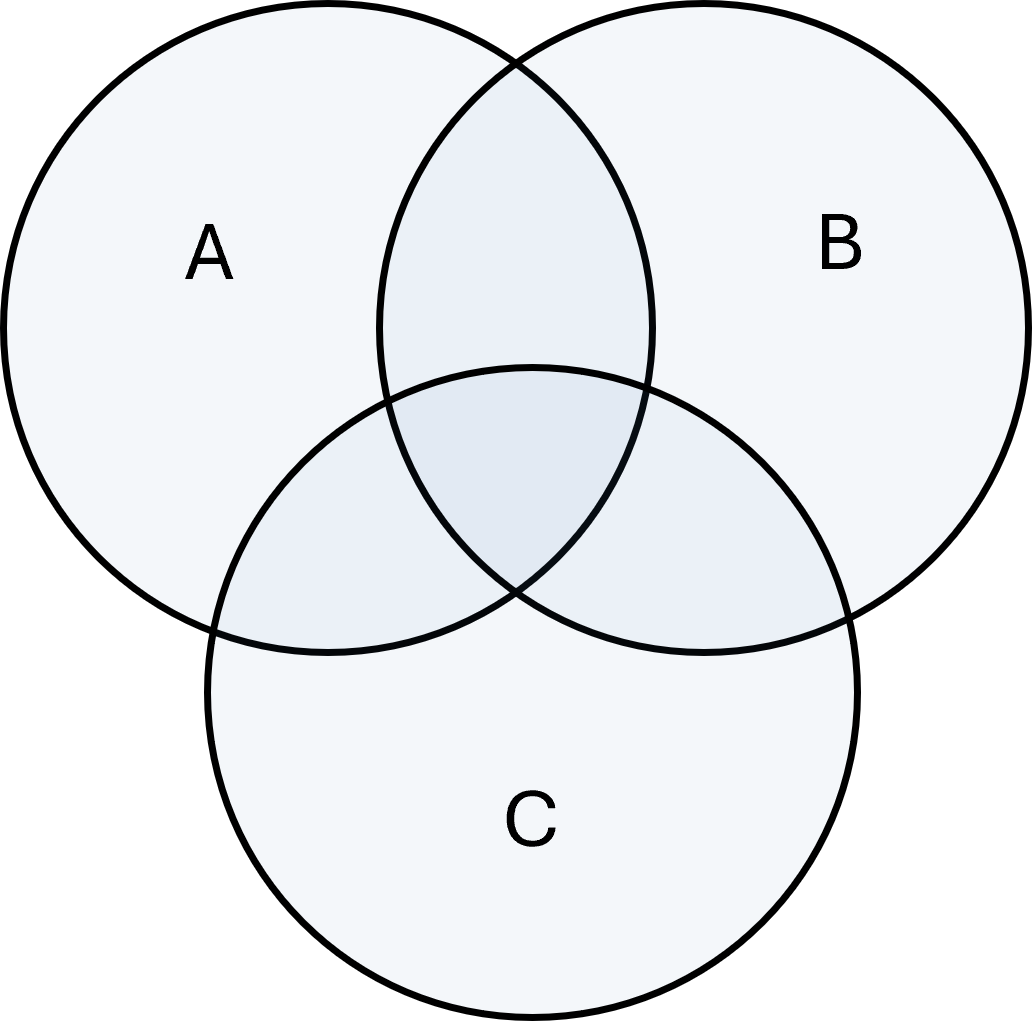
Diagrammes de Venn

Les diagrammes de Venn sont souvent utilisés pour illustrer graphiquement les opérations sur les ensembles.

Les cercles représentent des ensembles et les zones qui se chevauchent montrent comment fonctionnent l’union, l’intersection, la différence et le complément.