Une partie importante de la théorie des ensembles consiste à comparer et à combiner des ensembles. Ici, nous examinons les sous-ensembles, les sous-ensembles propres, les intersections, les ensembles puissance et le produit cartésien.

 

Sous-ensemble

Un ensemble \( \large A\) est un sous-ensemble d’un autre ensemble \( \large B\) si tous les éléments de \( \large A\) se trouvent aussi dans \( \large B\). Cela s’écrit :

 

$$ \large A \subseteq B $$

 

 

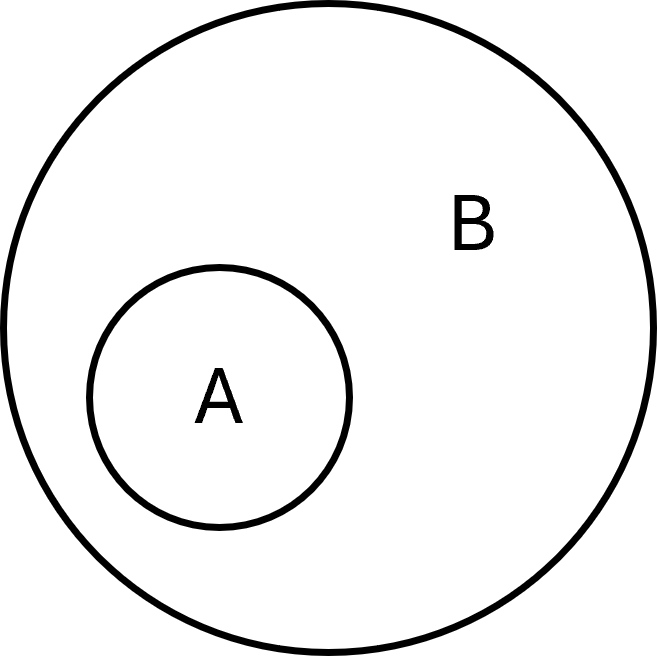
Formellement, cela peut se définir ainsi :

 

$$ \large A \subseteq B \;\;\Leftrightarrow\;\; \forall x \in A \Rightarrow x \in B $$

 

Exemples :

 

• \( \large \{1,2\} \subseteq \{1,2,3,4\}\)
• L’ensemble vide est toujours un sous-ensemble : \( \large \emptyset \subseteq A\) pour tout ensemble \( \large A\).

 

Remarque : Dans certains livres, le symbole \( \large \subset\) est utilisé à la place de \( \large \subseteq\) pour désigner les sous-ensembles. Ici, nous utilisons \( \large \subseteq\) comme norme.

 

 

Sous-ensemble propre

Un ensemble \( \large A\) est un sous-ensemble propre de \( \large B\) si \( \large A \subseteq B\) mais \( \large A \neq B\).

Cela signifie que \( \large B\) contient au moins un élément qui n’est pas dans \( \large A\).

La notation est :

 

$$ \large A \subset B $$

 

Exemple : \( \large \{1,2\} \subset \{1,2,3\}\).

 

 

Intersection

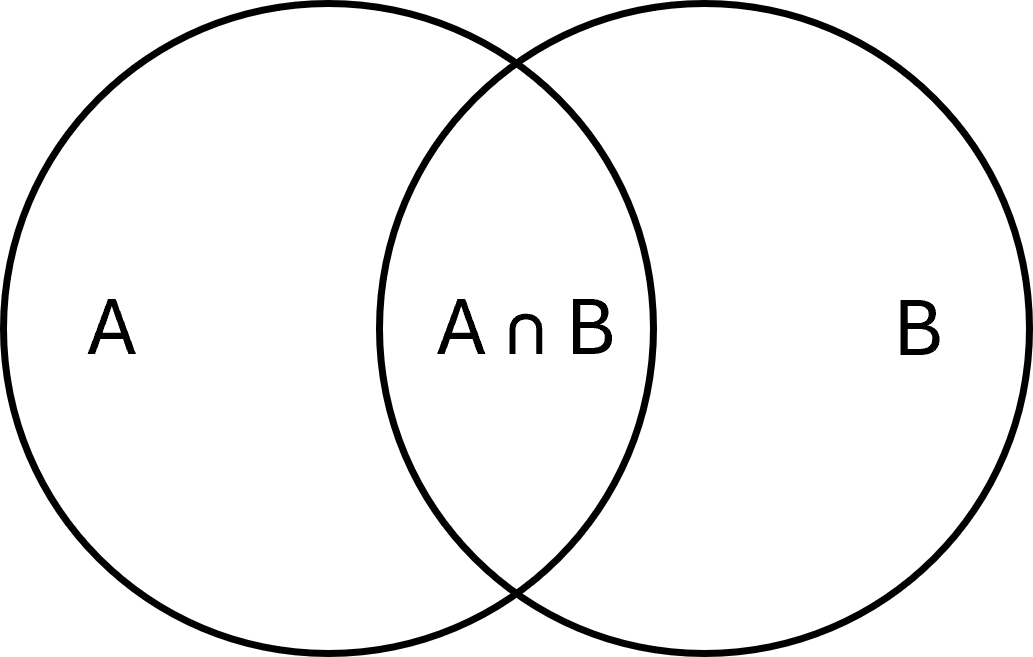
L’intersection de deux ensembles \( \large A\) et \( \large B\) est l’ensemble des éléments qui appartiennent aux deux ensembles. Elle s’écrit :

 

$$ \large A \cap B = \{x \mid x \in A \;\wedge\; x \in B\} $$

 

Exemple : Si \( \large A = \{1,2,3\}\) et \( \large B = \{3,4,5\}\), alors \( \large A \cap B = \{3\}\).

 

 

 

 

Ensemble puissance

L’ensemble puissance d’un ensemble \( \large A\) est l’ensemble de tous les sous-ensembles de \( \large A\).

Il s’écrit \( \large \mathcal{P}(A)\).

 

Si \( \large A = \{0,1\}\), alors :

 

$$ \large \mathcal{P}(A) = \{\emptyset, \{0\}, \{1\}, \{0,1\}\} $$

 

Le nombre d’éléments d’un ensemble puissance est \( \large 2^{|A|}\).

Par exemple, si \( \large |A| = 3\), alors \( \large \mathcal{P}(A)\) a \( \large 2^3 = 8\) éléments.

 

 

Produit cartésien

Le produit cartésien de deux ensembles \( \large A\) et \( \large B\) est l’ensemble de tous les couples ordonnés où la première composante provient de \( \large A\) et la seconde de \( \large B\).

Il s’écrit :

 

$$ \large A \times B = \{(a,b) \mid a \in A \;\wedge\; b \in B\} $$

 

Exemple : Si \( \large A = \{1,2\}\) et \( \large B = \{a,b\}\), alors :

 

$$ \large A \times B = \{(1,a),(1,b),(2,a),(2,b)\} $$

 

Remarque : l’ordre a de l’importance : \( \large A \times B \neq B \times A\) en général.