Volume avec des vecteurs

Le volume d’un solide dans l’espace peut être calculé à l’aide de vecteurs. En particulier, les parallélépipèdes (boîtes) peuvent s’exprimer par une formule simple lorsqu’ils sont décrits par trois vecteurs.

 

Volume d’un parallélépipède

Pour trois vecteurs \( \large \mathbf{u}, \mathbf{v}, \mathbf{w} \) dans l’espace, le volume du parallélépipède qu’ils engendrent est donné par :

 

$$ \large V = \left| \det \begin{pmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ z_1 & z_2 & z_3 \end{pmatrix} \right| $$

 

où \( \large \mathbf{u} = (x_1,y_1,z_1) \), \( \large \mathbf{v} = (x_2,y_2,z_2) \) et \( \large \mathbf{w} = (x_3,y_3,z_3) \).

 

 

Exemple

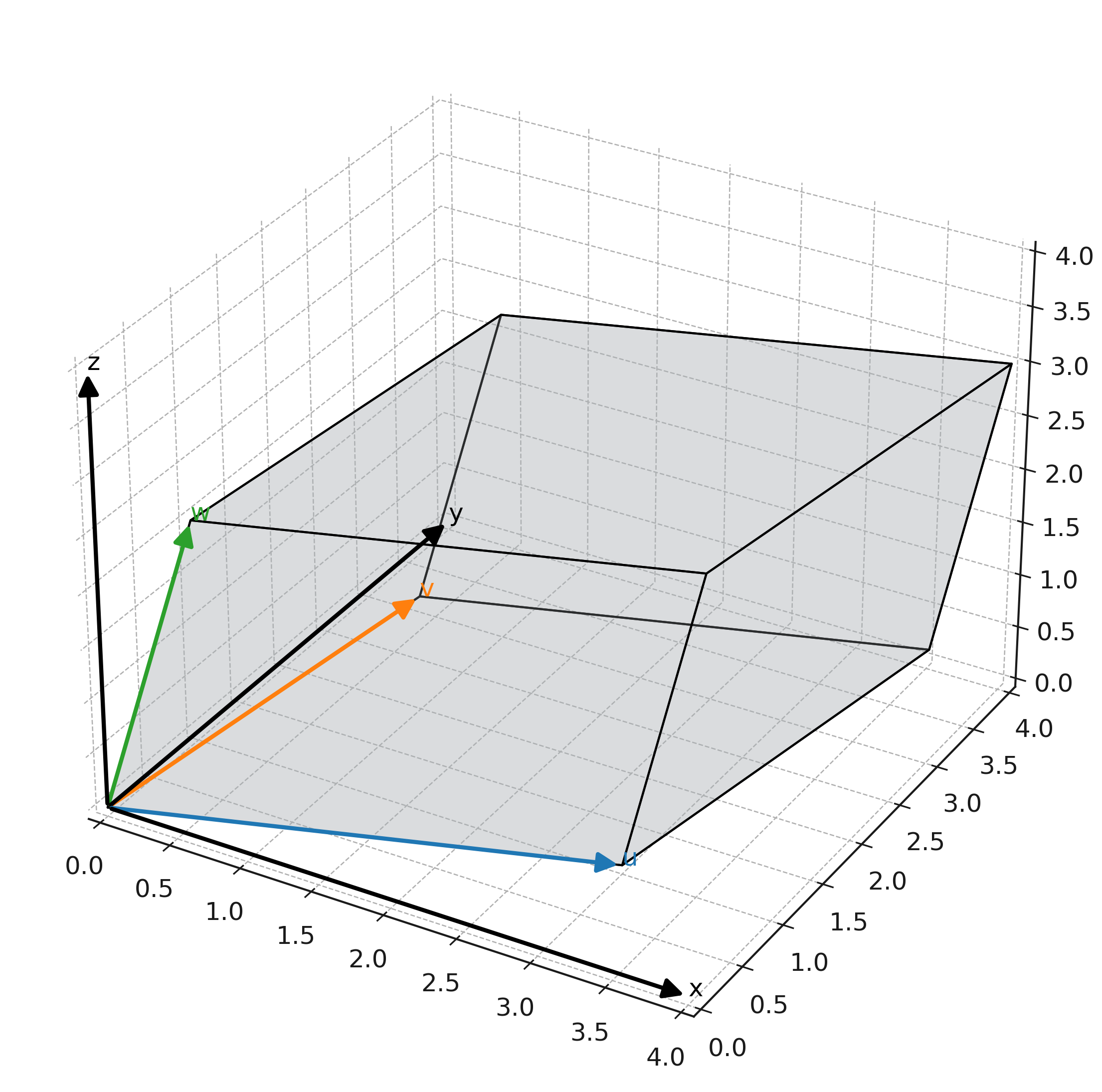
Nous prenons \( \large \mathbf{u} = (3,1,0) \), \( \large \mathbf{v} = (1,2,1) \) et \( \large \mathbf{w} = (0,1,2) \).

 

$$ \large V = \left| \det \begin{pmatrix} 3 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 2 \end{pmatrix} \right| $$

 

Lorsqu’on calcule un déterminant, on peut le développer selon n’importe quelle ligne ou colonne. Le résultat est toujours le même, quel que soit le choix. Pour simplifier, nous développons ici selon la première ligne.

 

$$ \large V= 3 \cdot \det \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} - 1 \cdot \det \begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix} + 0 \cdot \det \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix} $$

 

Les petits déterminants se calculent séparément :

$$ \large \det \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} = 2 \cdot 2 - 1 \cdot 1 = 3 $$

$$ \large \det \begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix} = 1 \cdot 2 - 1 \cdot 0 = 2 $$

 

Nous remplaçons maintenant les résultats dans l’expression :

 

$$ \large V = | 3 \cdot 3 - 1 \cdot 2 + 0 | = | 9 - 2 | = | 7 | = 7 $$

 

Le volume du parallélépipède est donc 7. Nous utilisons la valeur absolue, car un déterminant peut être négatif selon l’orientation des vecteurs, mais un volume ne peut jamais être inférieur à zéro.

 

 

Interprétation géométrique

La formule correspond au calcul aire de base multipliée par hauteur. L’aire de la base est obtenue par un calcul d’aire, et la hauteur est donnée en projetant le troisième vecteur perpendiculairement sur la base.

 

Application

Les formules de volume avec vecteurs sont utilisées en géométrie, algèbre linéaire et physique. Elles permettent de calculer le volume de boîtes et d’autres solides dans les systèmes de coordonnées, et constituent la base de thèmes ultérieurs tels que les déterminants, le produit vectoriel et les intégrales.