Droites et plans dans l’espace
Dans l’espace, les droites et les plans peuvent être décrits à l’aide de vecteurs. Cela permet de travailler de manière systématique avec la géométrie en trois dimensions.
Droites
Une droite dans l’espace peut être décrite par un point \( \large \mathbf{a} \) et un vecteur directeur \( \large \mathbf{r} \). Tous les points \( \large \mathbf{x} \) de la droite peuvent s’écrire comme
$$ \large \mathbf{x} = \mathbf{a} + t \cdot \mathbf{r}, \quad t \in \mathbb{R} $$
Ici, \( \large t \) est un paramètre qui détermine la distance parcourue le long de la droite.
Exemple
Une droite passant par le point \( \large (1,2,0) \) avec le vecteur directeur \( \large (2,-1,3) \) est donnée par :
$$ \large \mathbf{x} = (1,2,0) + t \cdot (2,-1,3) $$
Plans
Un plan peut être décrit par un point \( \large \mathbf{a} \) et un vecteur normal \( \large \mathbf{n} \). Tous les points \( \large \mathbf{x} \) du plan satisfont
$$ \large (\mathbf{x} - \mathbf{a}) \cdot \mathbf{n} = 0 $$
Cela signifie que la différence entre n’importe quel point du plan et le point \( \large \mathbf{a} \) est perpendiculaire au vecteur normal.
Exemple
Un plan passant par le point \( \large (1,0,2) \) avec le vecteur normal \( \large (2,-1,1) \) peut être décrit par
$$ \large 2(x-1) -1(y-0) + 1(z-2) = 0 $$
ou réécrit :
$$ \large 2x - y + z = 4 $$
Interprétation géométrique
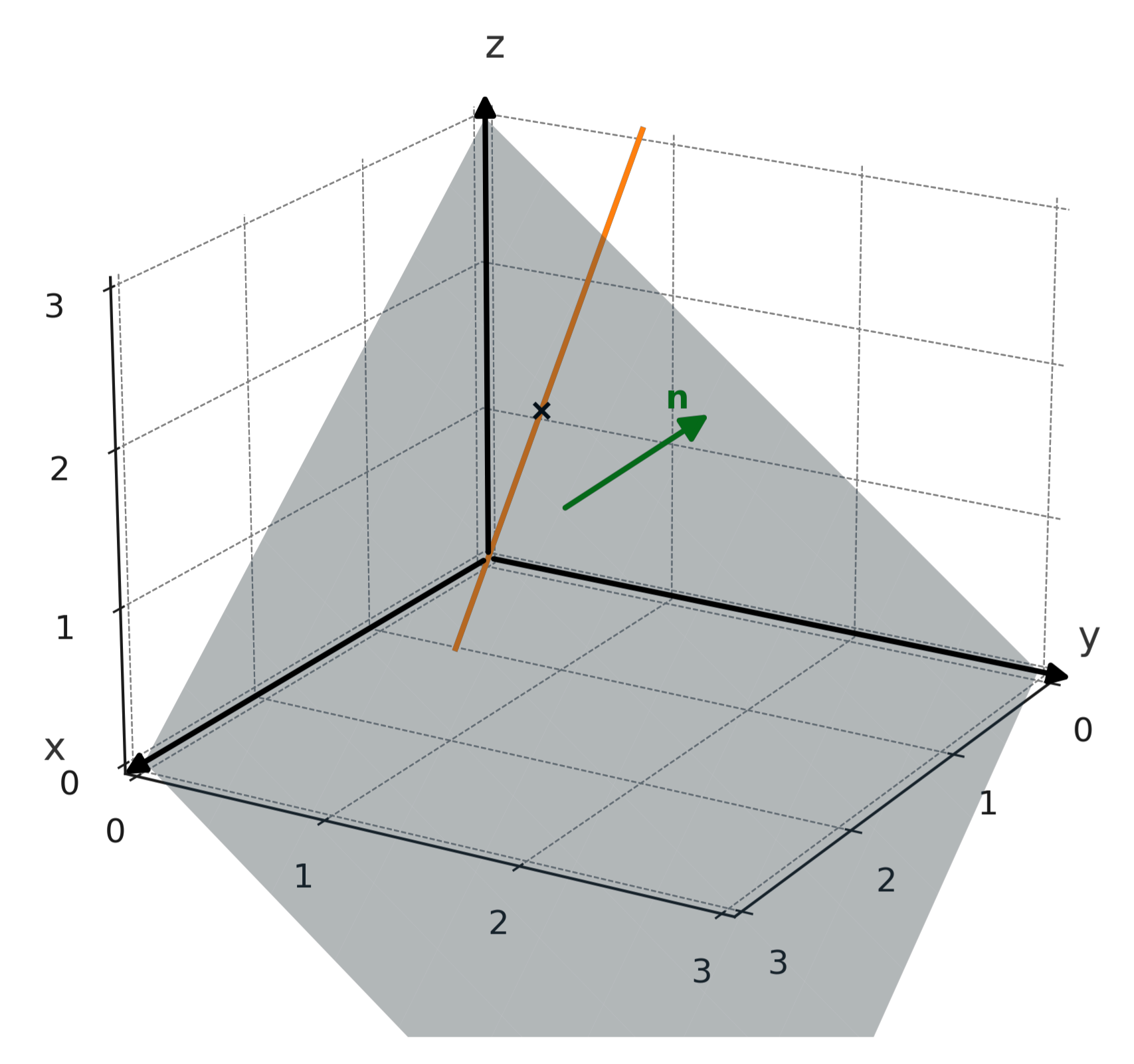
Une droite décrit tous les points le long d’une direction, tandis qu’un plan décrit tous les points dans une « couche plane » infinie. Le vecteur normal (n) d’un plan est perpendiculaire à cette surface.
L’intersection entre une droite et un plan peut être un seul point, marqué d’une croix sur l’illustration ci-dessous.
Elle peut aussi être toute la droite, si celle-ci appartient au plan, ou vide, si la droite est parallèle et extérieure au plan.
Application
Les droites et les plans dans l’espace sont essentiels en géométrie, en physique et en informatique. Ils sont utilisés, par exemple, pour décrire des trajectoires, des réflexions, la modélisation 3D et la détection de collisions en infographie.