Coordonnées en 3D
Dans l’espace 3D, un point est décrit par trois coordonnées. Alors que dans le plan nous utilisons deux nombres pour indiquer une position, dans l’espace il faut trois nombres pour déterminer un point de manière unique.
Définition
Un point \( \large P \) dans l’espace s’écrit
$$ \large P = (x,y,z) $$
Ici \( \large x \) est la distance le long de l’axe x, \( \large y \) la distance le long de l’axe y, et \( \large z \) la distance le long de l’axe z.
Exemple
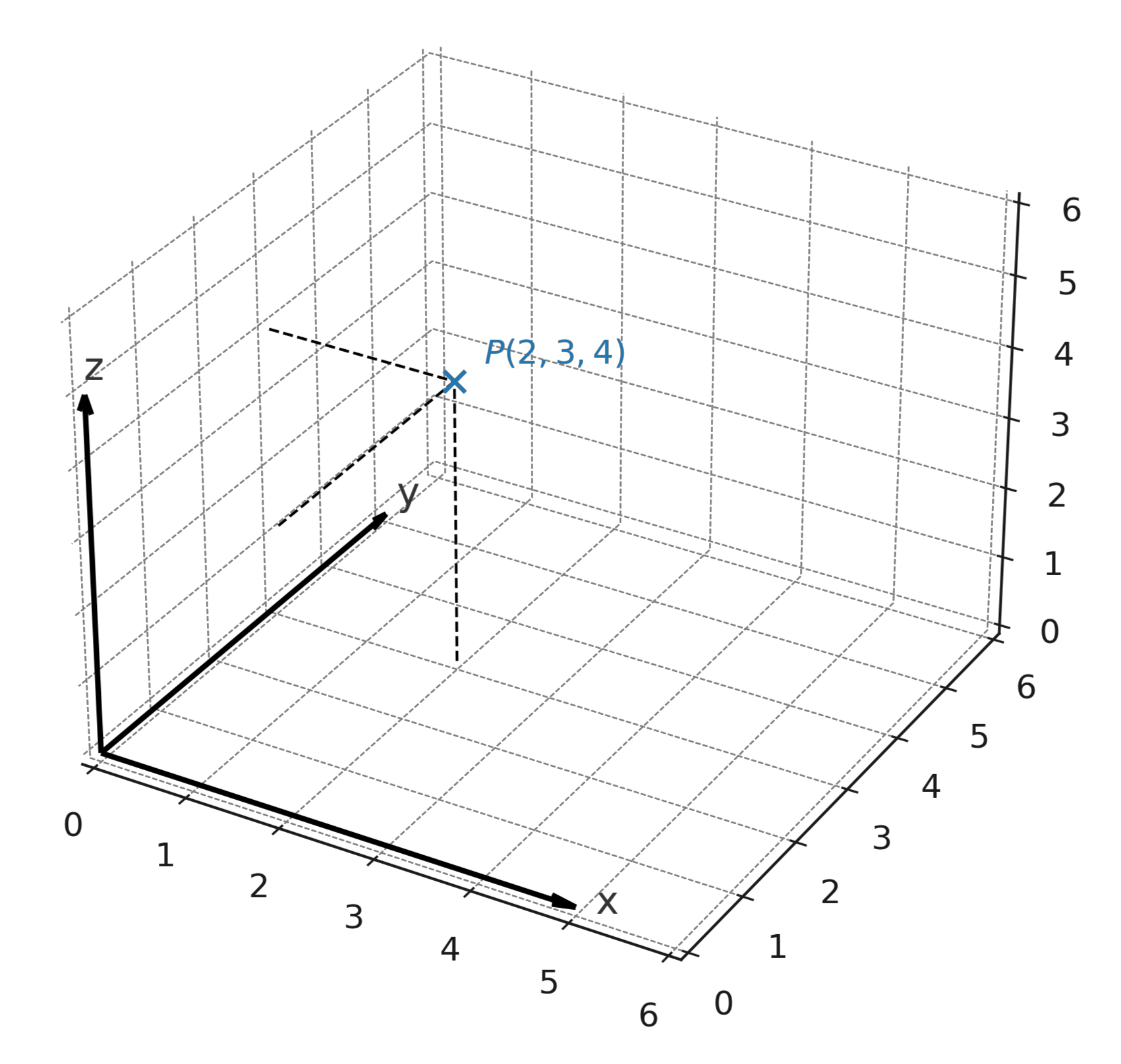
Le point \( \large P = (2,3,4) \) signifie avancer de 2 unités sur l’axe x, 3 unités sur l’axe y et 4 unités vers le haut sur l’axe z.
Axes de coordonnées et origine
Les trois axes sont appelés axe x, axe y et axe z. Leur point commun est appelé l’origine et a pour coordonnées
$$ \large O = (0,0,0) $$
Un vecteur de l’origine à un point \( \large P=(x,y,z) \) s’écrit
$$ \large \vec{OP} = (x,y,z) $$
Distance dans l’espace
La distance de l’origine à un point \( \large (x,y,z) \) se trouve en généralisant le théorème de Pythagore :
$$ \large |(x,y,z)| = \sqrt{x^2 + y^2 + z^2} $$
C’est la longueur du vecteur allant de l’origine au point.
Interprétation géométrique
Un système de coordonnées dans l’espace est construit à partir de trois axes mutuellement perpendiculaires. Chaque point peut être vu comme un sommet d’un prisme rectangulaire ayant l’origine comme point de départ.
Application
Les coordonnées en 3D sont utilisées partout en mathématiques, en physique et en informatique, par exemple pour décrire des points en géométrie, des positions dans l’espace ou des objets en graphiques 3D.