Produit scalaire
Le produit scalaire est une opération entre deux vecteurs qui donne un nombre. Il est utilisé pour calculer les angles entre vecteurs et pour déterminer s’ils sont perpendiculaires.
Définition
Pour deux vecteurs dans l’espace \( \large \mathbf{u} = (x_1,y_1,z_1) \) et \( \large \mathbf{v} = (x_2,y_2,z_2) \), le produit scalaire est défini comme
$$ \large \mathbf{u} \cdot \mathbf{v} = x_1x_2 + y_1y_2 + z_1z_2 $$
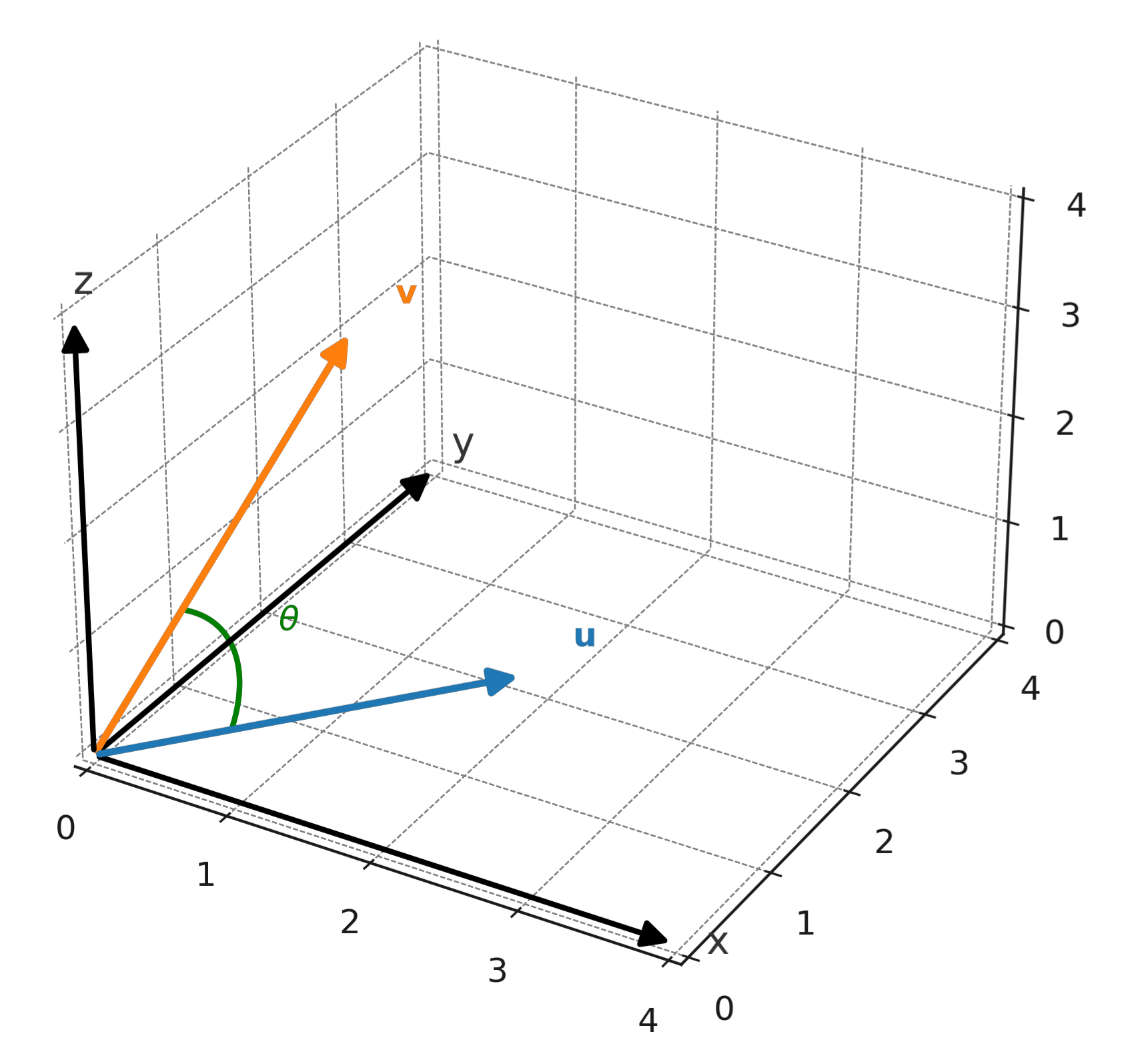
Une autre formule montre la relation avec l’angle entre les vecteurs :
$$ \large \mathbf{u} \cdot \mathbf{v} = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \cos(\theta) $$
où \( \large \theta \) est l’angle entre \( \large \mathbf{u} \) et \( \large \mathbf{v} \).
Exemple
Nous prenons \( \large \mathbf{u} = (1,2,3) \) et \( \large \mathbf{v} = (4,-1,2) \).
$$ \large \mathbf{u} \cdot \mathbf{v} = 1 \cdot 4 + 2 \cdot (-1) + 3 \cdot 2 = 4 - 2 + 6 = 8 $$
Le produit scalaire est 8.
Interprétation géométrique
Le produit scalaire mesure à quel point les deux vecteurs pointent dans la même direction. Si l’angle est inférieur à 90°, le produit scalaire est positif. Si l’angle est supérieur à 90°, le produit scalaire est négatif. Si les vecteurs sont perpendiculaires, le produit scalaire est nul.
Application
Le produit scalaire est utilisé dans de nombreux contextes, notamment pour trouver les angles entre vecteurs, déterminer l’orthogonalité et en physique pour calculer le travail effectué par une force le long d’un déplacement.