Produit vectoriel
Le produit vectoriel de deux vecteurs dans l’espace est un vecteur qui est perpendiculaire aux deux vecteurs originaux. Le produit vectoriel est utilisé pour trouver des aires, des vecteurs normaux et des orientations en géométrie 3D.
Définition
Pour deux vecteurs \( \large \mathbf{u} = (x_1,y_1,z_1) \) et \( \large \mathbf{v} = (x_2,y_2,z_2) \), le produit vectoriel est défini par le déterminant :
$$ \large \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix} = (y_1z_2 - z_1y_2,\; z_1x_2 - x_1z_2,\; x_1y_2 - y_1x_2) $$
Exemple
Nous prenons \( \large \mathbf{u} = (1,2,3) \) et \( \large \mathbf{v} = (4,5,6) \).
$$ \large \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 2 & 3 \\ 4 & 5 & 6 \end{vmatrix} = (-3,6,-3) $$
Le résultat est un nouveau vecteur \( \large (-3,6,-3) \), qui est perpendiculaire à la fois à \( \large \mathbf{u} \) et à \( \large \mathbf{v} \).
Interprétation géométrique
La longueur du produit vectoriel correspond à l’aire du parallélogramme engendré par les vecteurs :
$$ \large |\mathbf{u} \times \mathbf{v}| = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \sin(\theta) $$
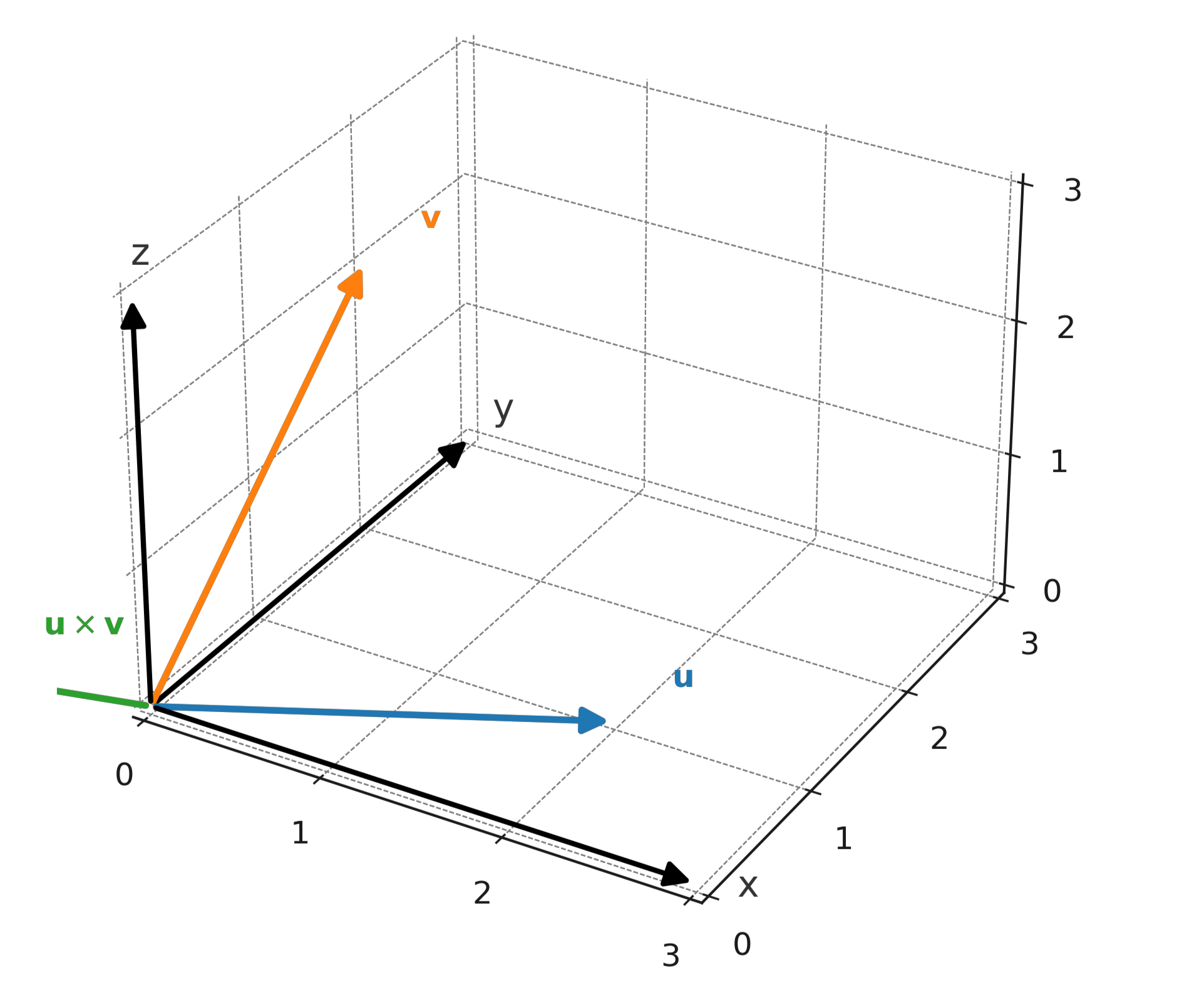
La direction est déterminée par la règle de la main droite : si l’on pointe l’index de la main droite dans la direction de \( \large \mathbf{u} \) et le majeur dans la direction de \( \large \mathbf{v} \), alors le pouce indique la direction de \( \large \mathbf{u} \times \mathbf{v} \).
Application
Le produit vectoriel est utilisé dans de nombreux domaines des mathématiques et de la physique :
- Pour trouver un vecteur normal à un plan
- Pour calculer l’aire de parallélogrammes et de triangles en 3D
- En mécanique pour déterminer le moment d’une force
- En infographie pour calculer l’orientation des surfaces