Équations différentielles numériques (Euler, Runge-Kutta)

Lorsqu’une équation différentielle ne peut pas être résolue analytiquement, il est possible de trouver une solution approchée à l’aide de méthodes numériques. Ces méthodes calculent les valeurs de la fonction point par point à partir de l’équation différentielle et d’une condition initiale. Deux des plus utilisées sont la méthode d’Euler et la méthode de Runge–Kutta.

 

 

Idée des équations différentielles numériques

Une équation différentielle ordinaire simple a la forme :

 

$$ \large y' = f(x,y) $$

 

Si une valeur initiale \( \large y(x_0) = y_0 \) est connue, on peut utiliser \( \large f(x,y) \) pour calculer comment \( y \) change lorsque \( x \) augmente légèrement. Ce processus est répété pas à pas afin de construire progressivement une solution numérique.

 

 

Méthode d’Euler

La méthode d’Euler est la solution numérique la plus simple. Elle utilise directement l’équation différentielle pour calculer la valeur suivante :

 

$$ \large y_{n+1} = y_n + h \cdot f(x_n, y_n) $$

 

Ici \( \large h \) est la taille du pas. En répétant le processus avec de nombreux petits pas, on peut tracer une courbe approchée de \( y(x) \).

 

 

Exemple de la méthode d’Euler

Nous voulons résoudre \( \large y' = y \) avec la condition initiale \( \large y(0) = 1 \) et \( \large h = 0{,}5 \).

 

Pour chaque pas :

 

$$ \large y_{n+1} = y_n + 0{,}5 \cdot y_n = 1{,}5y_n $$

 

Après quatre pas, on obtient :

 

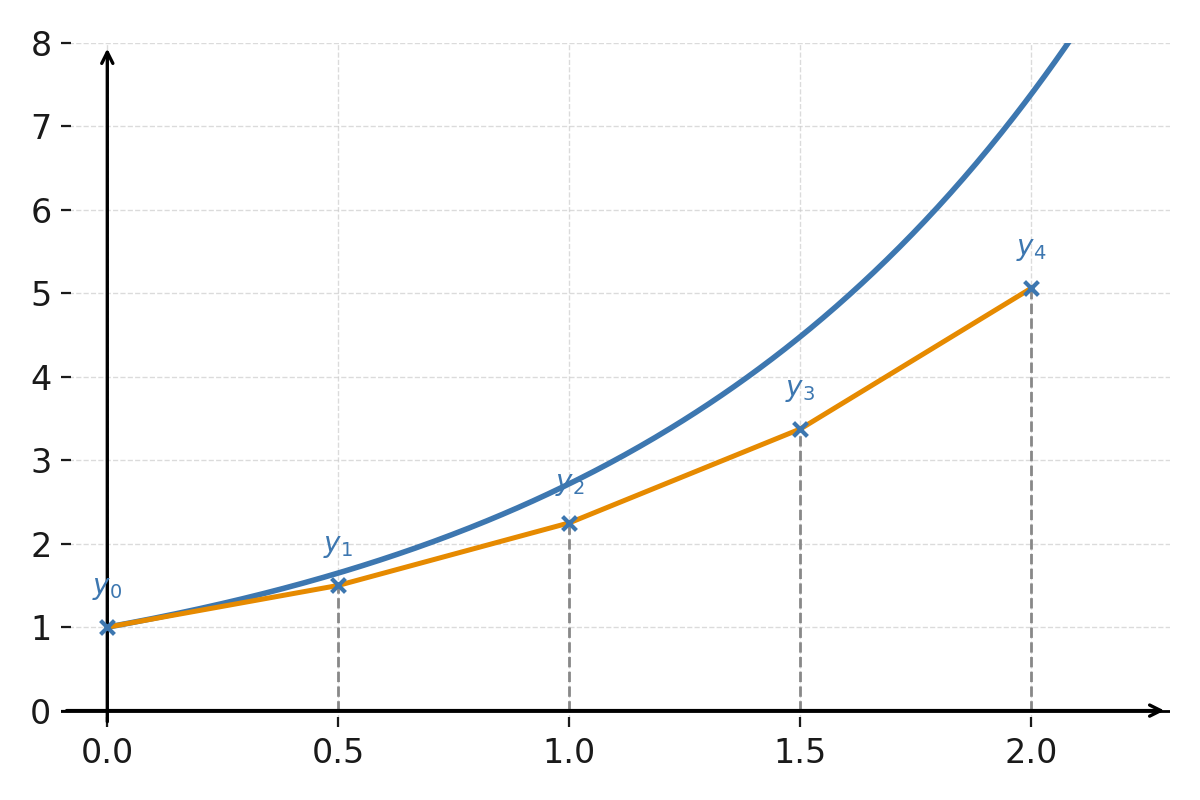
$$ \large y_1 = 1{,}5, \quad y_2 = 2{,}25, \quad y_3 = 3{,}375, \quad y_4 = 5{,}0625 $$

 

La solution exacte est \( \large y = e^x \), et pour \( \large x=2 \), on obtient \( \large e^2 \approx 7{,}389 \). La méthode d’Euler sous-estime donc la courbe réelle, car chaque pas utilise une ligne droite au lieu de la fonction courbée.

 

 

 

 

Méthode de Runge–Kutta (4e ordre)

Pour une meilleure précision, on peut utiliser la méthode de Runge–Kutta du 4e ordre (RK4). Elle prend la moyenne de quatre pentes au lieu d’une seule :

 

$$
\large
\begin{aligned}
k_1 &= f(x_n, y_n) \\[8pt]
k_2 &= f\!\left(x_n + \frac{h}{2},\, y_n + \frac{h}{2}k_1\right) \\[8pt]
k_3 &= f\!\left(x_n + \frac{h}{2},\, y_n + \frac{h}{2}k_2\right) \\[8pt]
k_4 &= f\!\left(x_n + h,\, y_n + h k_3\right) \\[8pt]
y_{n+1} &= y_n + \frac{h}{6}\!\left(k_1 + 2k_2 + 2k_3 + k_4\right)
\end{aligned}
$$

 

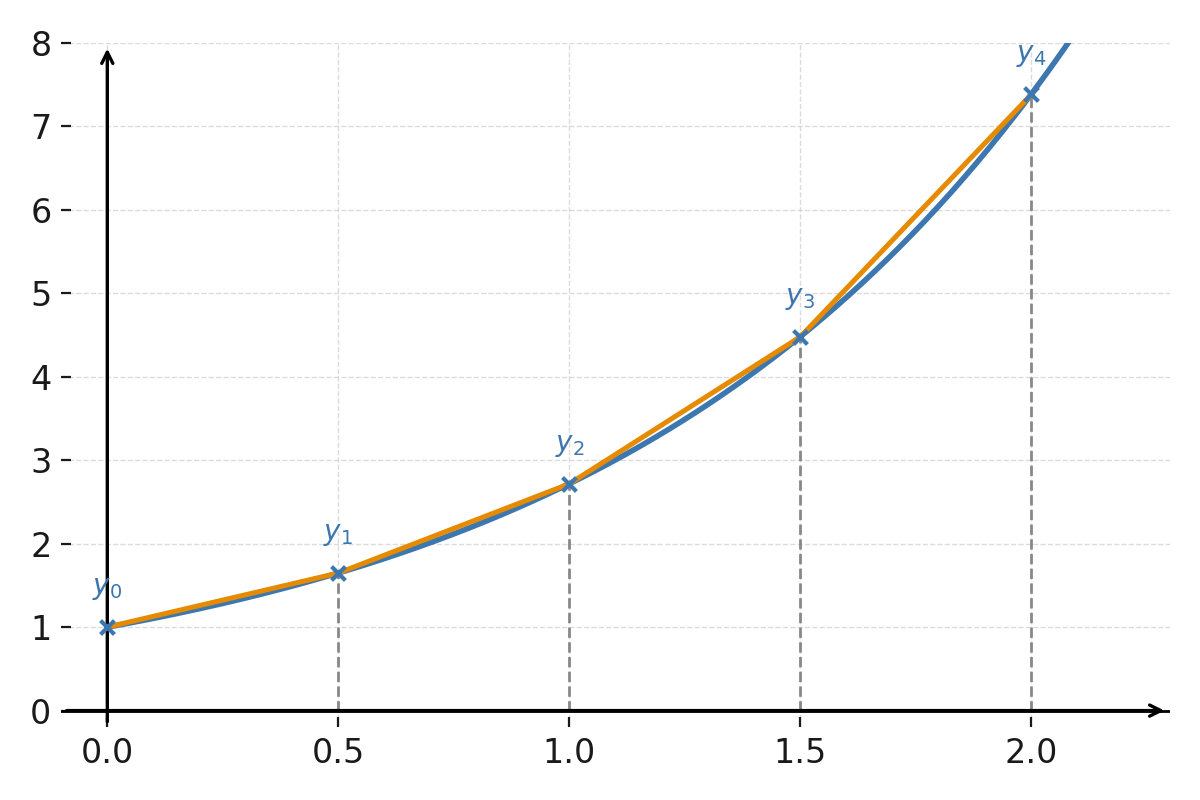
RK4 est beaucoup plus précise que la méthode d’Euler, même avec peu de pas, et elle est donc très utilisée en pratique.

 

 

 

 

Remarques

Les équations différentielles numériques sont parmi les outils les plus importants des mathématiques appliquées, de la physique et de l’ingénierie. Elles servent à simuler des systèmes pour lesquels on connaît le taux de variation, mais où il n’existe pas de formule fermée pour la fonction elle-même.